Pregunta 31. Encuentra el punto de la parábola x 2 = 2y que está más cerca del punto (0, 5).
Solución:
x2 = 2y ……(yo)
Sea P(x, y) un punto en la curva dada, y
Q sea el cuadrado de la distancia entre P y A( 0, 5 ).
Q = x² + (y – 5) 2 ……..(ii)
= 2y + (y – 5) 2
Al diferenciar wrt y, obtenemos
dQ/dy = 2 + 2(y – 5)
Para máximos y mínimos,
Ponga dQ/dy = 0
⇒ 2 + 2y – 10 = 0
⇒ y = 4
Ahora,
Cuando y = 4, d 2 Q/dy 2 = 2 > 0
Entonces, y = 4 es el punto de mínimos locales
Ahora pon el valor de y en la ecuación (1), obtenemos
x = ±2√2
Entonces, P(±2√2, 4) es el punto más cercano en la curva a A(0, 5).
Pregunta 32 Encuentra las coordenadas de un punto en la parábola y = x 2 + 7x + 2 que está más cerca de la línea recta y = 3x – 3.
Solución:
La ecuación dada de la parábola es
y = x 2 + 7x + 2 ……(yo)
más cercano a la línea recta y = 3x – 3 ……(ii)
Consideremos que P(x, y) es el punto de la parábola dada que está más cerca de la línea y = 3x – 3
Sea Q la distancia perpendicular de P a la recta y = 3x – 3
Q =
=
Al derivar wrt x, obtenemos
dQ/dx = (2x +4) / √10
Para máximos o mínimos, tenemos
Ponga dQ/dx = 0
⇒ (2x + y)/√10 = 0
⇒ x = -2
Ahora pon el valor de x en la ecuación (i), obtenemos
y = 4 – 14 + 2 = -8
Cuando x = -2 y y = -8, d 2 Q/dx 2 = 2/√10 > 0
Entonces, x = -2, y y = -8 es el punto de los mínimos locales,
Por lo tanto, P(-2, -8) es el punto de la parábola más cercano a la línea y = 3x-3.
Pregunta 33 Encuentra el punto en la curva y 2 = 2x que está a una distancia mínima del punto (1, 4).
Solución:
La ecuación dada de la curva es
y 2 = 2x …..(yo)
Sea P(x, y) un punto en la curva dada, que está a la distancia mínima del punto A(1, 4) y
Q cuadrado de la longitud de AP
Q = (x – 1) 2 + (y – 4) 2
= x2 + 1 – 2x +y2 +16 – 8y
= x2 – 2x +2x+17 – 8y
= y 4 /4 – 8y +17 [Ya que y 2 = 2x]
Al diferenciar wrt y, obtenemos
dQ/dy = y 3 – 8
Para máximos y mínimos tenemos
Ponga dQ/dy = 0
y 3 – 8 = 0
y 3 = 2 3
y = 2
Cuando y = 2, d 2 S/dy 2 = 3y 2 = 12 > 0
Entonces, y = 2 es el punto de los mínimos locales,
Tenemos
x = y 2 /2 = 4/2 = 2
Por tanto, P(2, 2) está a una distancia mínima del punto A(1, 4).
Pregunta 34. Encuentra la pendiente máxima de la curva y = -x 3 + 3x 2 + 2x – 27.
Solución:
La ecuación dada de la curva es
y = x 3 + 3x 2 + 2x – 27 …..(i)
La pendiente de la ecuación dada de la curva es
m = dy/dx = −3x 2 + 6x + 2 …..(ii)
Al derivar wrt x, obtenemos
dm/dx = -6x + 6
Nuevamente diferenciando wrt x, obtenemos
d 2 m/dx 2 = -6 < 0
Para máximos y mínimos,
Poner dm/dx = 0
⇒ -6x + 6 = 0
⇒ x = 1
Cuando x = 1, d 2 m/dx 2 = -6 < 0
Entonces, x = 1 es el punto de los máximos locales
Por lo tanto, la pendiente máxima de la curva dada es = -3 + 6 + 2 = 5
Pregunta 35. El costo total de producir x radios por día es (x 2/4 + 35x + 25) y el precio por equipo al que se pueden vender es (50 – x/2). Encuentre la producción diaria para maximizar la ganancia total.
Solución:
Dado,
El costo de producir x aparatos de radio es Rs. x 2 /4 + 35x + 25
Y el precio de venta de x radio es Rs. x(50 – x/2)
Asi que,
La ganancia en x aparatos de radio es
P = 50x – x 2 /2 – x 2 /4 -35x – 25
Al diferenciar wrt y, obtenemos
dp/dx = 50 – x – x/2- 35
= 15 – 3x/2
Para máximos y mínimos,
Poner, dp/dx = 0
⇒ 15 – 3x/2 = 0
⇒ x = 10
Cuando x = 10, d 2 p/dx 2 = -3/2 <0
Entonces, x = 10 es el punto de los máximos locales
Por lo tanto, la ganancia es máxima solo si la producción diaria es 10.
Pregunta 36. Los fabricantes pueden vender x artículos a un precio de (5 – x/100) cada uno. El precio de costo es (x/5 + 500). Encuentre la cantidad de artículos que debe vender para obtener la máxima ganancia.
Solución:
Consideremos que S(x) es el precio de venta de x artículos y C(x) el precio de costo de x artículos.
Entonces, se da que
S(x) = (5 – x/100) = 5x – x 2 /100
y
C(x)= x/5 + 500
Entonces la función de beneficio es
P(x) = S(x) – C(x)
= 5x – x 2 /100 -x/5 – 500 = 24x/5 – x 2 /100 – 500
Al derivar wrt x, obtenemos
P'(x) = 24/5 – x/50
También p”(x) = – 1/50
Para máximos y mínimos,
Ponga, P'(x) = 0
⇒ 24/5 – x/50 = 0
⇒ x = 24/5 × 50 = 240
Cuando x = 240, P”(240) = -1/50 < 0
Entonces, x = 240 es un punto de máximos.
Por lo tanto, cuando el fabricante vende 240, puede obtener el máximo beneficio.
Pregunta 37. Se va a construir un tanque abierto con una base cuadrada y lados verticales para contener una cantidad dada de agua. Muestre que los gastos de revestimiento con plomo serán mínimos si la profundidad se hace a la mitad del ancho.
Solución:
Consideremos que l es la longitud del lado de la base cuadrada del tanque y h la altura del tanque.
Entonces, el volumen del tanque es
V = l 2 h ……(i)
y la superficie total es
A = l2 + 4lh …..(ii)
Ahora,
De la ecuación (i) y (ii), obtenemos
A = l 2 + 4v/l
Al diferenciar wrt l, obtenemos
dA/dl = 2l – 4v/l 2
Además, d 2 A/dl 2 = 2 + 8v/l 3
Para máximos y mínimos,
Poner, dA/dl = 0
⇒ 2l – 4v/l2 = 0
⇒ 2l 3 – 4v = 0
⇒ l 3 = 2v = 2t 2 h
⇒ l 2 [ l – 2h ]= 0
⇒ l = 0 o 2h
Aquí, l = 0 no es posible
En l = 2h, d 2 S/dl 2 > 0
Entonces, l = 2h es el punto de los mínimos locales
Por tanto, la superficie total es mínima cuando l = 2h
Pregunta 38. Una caja de volumen constante c debe tener el doble de largo que de ancho. El material de la parte superior y los cuatro lados cuesta tres veces más por metro cuadrado que el de la parte inferior. ¿Cuáles son las dimensiones más económicas?
Solución:
Consideremos que ABCDEFGH es una caja de volumen constante c y se da que la caja mide el doble de largo que de ancho.
Entonces, BF = x y AB = 2x
Entonces, el costo del material de la parte superior y frontal = 3 x costo del material de la parte inferior de la caja.
⇒ 2x × x + xh + xh+ 2xh + 2xh = 3 × 2x 2
⇒ 2x 2 + 2xh + 4xh = 6x 2
⇒ 4x 2 – 6xh = 0
⇒ 2x(2x – 3h) = 0
⇒ x = 3h/2 o h = 2x/3
volumen de la caja es
V = 2x × x × h
c = 2x 2 horas
h = c/2x 2 ……(yo)
Ahora,
La superficie de la caja es
A = 2 (2x 2 + 2xh + xh)
= 2( 2×2 + 3xh)
= 2(2x 2 + 3xc/2x 2 )
= 2(2x 2 + 3/2 × c/x)
Al derivar wrt x, obtenemos
dA/dx = 2(4x – 3/2 × c/x 2 )
Para máximos y mínimos,
Poner dA/dx = 0
2(4x – 3/2 × c/x2 ) = 0
8x 3 – 3c = 0
x = (3c/8) 1/3
Cuando x = (3c/8) 1/3 , d 2 A/dx 2 = 2 (4 + 3 × C/x 3 ) > 0
Entonces, x = (3c/8) 1/3 es el punto de mínimos locales
Por lo tanto, la dimensión más económica será
x = ancho = (3c/8) 1/3
2x = longitud = 2(3c/8) 1/3
h = altura = 2x/3 = 2/3 × (3c/8) 1/3
Pregunta 39. Se da la suma de las áreas superficiales de una esfera y un cubo Demostrar que cuando la suma de sus volúmenes es menor, el diámetro de la esfera es igual a la arista del cubo.
Solución:
Consideremos S la suma de las superficies de una esfera y un cubo.
S = 4πr 2 + 6l 2 …..(i)
Aquí, soy el lado del cubo y r el radio de la esfera
y V el volumen de la esfera y el cubo
V = 4/3πr 3 + l 3 …..(ii)
Al diferenciar wrt r, obtenemos
Para máximos y mínimos,
Poner dV/dr = 0
⇒ 4πr 2 = π/6(S – 4πr 2 ) 1/2 × 2r = 0
⇒ 2rπ[2r – I] = 0
r = 0, l/2
Ahora,
En r = I/2, d 2 V/dr 2 > 0
Entonces, r = I/2 es el punto de mínimos locales
Por lo tanto, el volumen es mínimo cuando l = 2r
Pregunta 40. Una cantidad dada de metal se va a moldear en un medio cilindro con una base rectangular y extremos semicirculares. Muestre que para que el área total de la superficie sea mínima, la relación entre la longitud del cilindro y el diámetro de sus extremos semicirculares es π:(π + 2)
Solución:
Sea ABCDEF un medio cilindro de base rectangular y extremos semicirculares.
Entonces, AB = altura del cilindro = h
Consideremos r el radio del cilindro.
Como sabemos que el volumen del medio cilindro es
V = 1/ 2πr 2h
2V/πr2 = h
El área total de la superficie del medio cilindro es
A = LSA del medio cilindro + área de dos extremos semicirculares + área del rectángulo (base)
A = πrh + πr 2 /2 + πr 2 /2 +h 2 r
= (πr + 2r)h + πr 2
= (π + 2)2v/πr + πr 2
Al diferenciar wrt r, obtenemos
dA/dr = [(π + 2)2v/π(-1/r 2 ) + 2πr]
Para máximos y mínimos,
Poner dA/dr = 0
⇒ [(π + 2)2v/π(-1/r 2 ) + 2πr] = 0
⇒ [(π+2)2v/πr 2 = 2πr
Pero 2r = D
h : re = π : π + 2
Nuevamente diferenciando wrt r, obtenemos
d 2 A/dr 2 = (π + 2)v/π × 2/r 3 + 2π > 0
Entonces, S será mínimo cuando h : 2r es π : π-12.
Por lo tanto, la altura del cilindro : Diámetro del extremo circular π : π + 2
Pregunta 41. La resistencia de una viga varía como el producto de su ancho y el cuadrado de su profundidad. Encuentre las dimensiones de la viga más fuerte que se puede cortar de un tronco circular de radio a.
Solución:
Consideremos ABCD como el área de la sección transversal de la viga que se corta de un tronco circular de radio a.
Entonces, AO = a y AC = 2a
Sea x el ancho y y la profundidad del tronco. Además, sea S la fuerza de la viga
Según la pregunta,
S = xy 2 …..(i)
en ΔABC
x 2 + y 2 = (2a) 2
⇒ y = (2a) 2 – x 2 …..(ii)
De la ecuación (i) y (ii), obtenemos
S = x((2a) 2 – x2 )
Al derivar wrt x, obtenemos
⇒ dS/dx = (4a 2 – x 2 ) – 2x 2
⇒ dS/dx = 4a 2 – 3x 2
Para máximos o mínimos
Ponga, dS/dx = 0
⇒ 4a 2 – 3x 2 = 0
⇒x2 = 4a 2/3 _
x = 2a√3
Ahora pon el valor de x en la ecuación (ii)
y 2 = 4a 2 – 4a 2 /3 = 8a 2 /3
y = 2a×√(2/3)
Ahora,
En x = 2a/√3, y = √(2/3)2a, d 2 S/dx 2 = -6x = -12a/√3 < 0
Entonces, (x = 2a/√3, y = √(2/3)2a) es el punto de máximos locales.
Por lo tanto, la dimensión de la viga más fuerte es 2a/√3 y √(2/3)2a.
Pregunta 42. Se traza una línea recta a través de un punto dado P(1, 4). Determina el valor mínimo de la suma de las intersecciones en los ejes de coordenadas.
Solución:
Consideremos que l es una línea que pasa por el punto P (1, 4) que corta el eje x y el eje y.
Entonces, la ecuación de la línea (l) es
y-4 = m(x-1)
La intersección x es (m – 4)/m y la intersección y es (4-m)
Sea S = (m – 4)/m + 4 – m
Al diferenciar wrt m, obtenemos
dS/dm = 4/m2 – 1
Para máximos y mínimos,
Ponga, dS/dm = 0
⇒ 4/m2 -1 = 0
⇒ metro = ±12
Ahora,
d 2 S/dm 2 = -8/m 3
En m = 2, d 2 S/dm 2 = -1 < 0
En m = -2, d 2 S/dm 2 = 1 > 0
Entonces, m = -2 es el punto de los mínimos locales.
Por lo tanto, el valor mínimo de la suma de la intersección es
= (m – 4)/m + 4 – m
= 3 + 6 = 9
Pregunta 43. El área total de una página es 150 cm 2 . El ancho combinado del margen superior e inferior es de 3 cm y el lateral de 2 cm. ¿Cuáles deben ser las dimensiones de la página para que el área del material impreso sea máxima?
Solución:

Dado que el área de la página PQRS en 150 cm 2
Además, AB + CD = 3 cm
EF + GH = 2 cm
Consideremos que x e y son el ancho combinado del margen en la parte superior e inferior y los lados
x = 3 cm y y = 2 cm.
Ahora, encontramos el área de material impreso = área de P’Q’R’S’
⇒ A = P’Q’ Q’R’
⇒ A = (b – y)(l – x)
⇒ A = (b – 2)(l – 3) …..(i)
También,
El área de PQRS = 150 cm 2
⇒ lb = 150 …..(ii)
De la ecuación (i) y (ii), obtenemos
A = (b – 2)(150/b – 3)
Al diferenciar wrt b, obtenemos
dA/db = (150/b – 3) + (b – 2)(- 150/b 2 )
Para máximo y mínimo,
Poner dA/db = 0
⇒ (150 – 3b)/b + (-150)(b – 2)b 2 = 0
⇒ 150b – 3b 2 – 150b +300 = 0
⇒ -3b 2 + 300 = 0
⇒ segundo = 10
De la ecuación (ii), obtenemos
l = 15
Ahora,
re 2 A/db 2 = -150/b2 – 150[-1/b2 + 4/b3]
Cuando b = 10, d 2 A/db 2 = -15/10 – 150[-1/100 + 4/1000] = -1,5 + 9 = -0,6 < 0
Entonces, b = 10 es el punto de los máximos locales.
Por lo tanto, la dimensión requerida será de 15 cm y 10 cm.
Pregunta 44. El espacio s descrito en el tiempo t por una partícula que se mueve en línea recta está dado por s = t 5 – 40t 3 + 30t 2 + 80t – 250. Encuentra el valor mínimo de aceleración.
Solución:
Dado que s es el espacio en el tiempo t por una partícula en movimiento es
S = t 5 – 40 t 3 +30 t 2 +80 t – 250
Velocidad = dS/dt = 5t 4 -120t 2 + 60t + 80
Aceleración = a = d 2 S/dt 2 = 20t 3 – 240t + 60t …..(i)
Ahora,
da/dt = 60t 2 – 240
Para máximos y mínimos,
Ponga, da/dt = 0
⇒ 60t 2 – 240 = 0
⇒ 60(t 2 – 4) = 0
⇒ t = 2
Ahora,
d2a / dt2 = 120t
En t = 2, d 2 a/dt 2 = 240 > 0
Entonces, t = 2 es el punto de mínimos locales
Por lo tanto, la aceleración mínima es 160 – 480 + 60 = -260
Pregunta 45. Una partícula que se mueve en línea recta tal que su distancia s en cualquier momento t está dada por s = t 4 /4 – 2t 3 + 4t 2 – 7. Encuentra cuándo su velocidad es máxima y su aceleración mínima.
Solución:
Dado que
Distancia(S) = t 4 /4 – 2t 3 + 4t 2 – 7
Velocidad (V) = dS/dt = t 3 – 6t 2 + 8t
Aceleración(a) = d 2 S/dt 2 = 3t 2 – 12t + 8
Para que la velocidad sea máxima y mínima,
Poner dV/dt = 0
⇒ 3t 2 – 12t +8 = 0
⇒ t =
= 2 ± 4√3/6
t = (2 + 2/√3), (2 – 2/√3)
Ahora,
d 2 V/dt 2 = 6t – 12
En t = (2 – 2/√3), d 2 V/dt 2 = 6(2 – 2/√3) – 12 = -12/√3 < 0
t = (2 + 2/√3), d 2 V/dt 2 = 6(2 + 2/√3) – 12 = 12/√3 > 0
Entonces, en t = (2 – 2/√3), la velocidad es máxima
Para que la aceleración sea máxima y mínima.
Poner da/dt = 0
⇒ 6t – 12 = 0
⇒ t = 2
Ahora,
Cuando, t = 2, d 2 a/dt 2 = 6 > 0
Por tanto, en t = 2, la aceleración es mínima.
Publicación traducida automáticamente
Artículo escrito por rahulsharma1771996 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
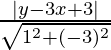

![Rendered by QuickLaTeX.com \frac{d^2V}{dr^2}=8πr-\frac{2π}{√6}[(S-4πr^2)^{\frac{1}{2}}]-\frac{8πr^2}{2(S-4πr^2)^{\frac{1}{2}}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3d9e7a4ca7ba3ce060ad5668fd616ce0_l3.png)
