Pregunta 1. Integre las siguientes integrales con respecto a x:
(i) ∫ x 4 dx
Solución:
∫ x 4 dx = x 4+1 /(4+1) + constante
= x 5 /5 + C
(ii) ∫ x 5/4 dx
Solución:
∫ x 5/4 dx = x 5/4 + 1 /(5/4 +1) + Constante
= 4/9 x 9/4 + C
(iii) ∫ 1/x 5 dx
Solución:
∫ 1/x 5 dx = ∫ x -5 dx
= x -5+1 /(-5+1) + Constante
= x -4 /(-4)+ C
= -1/(4x 4 ) + C
(iv) ∫ 1/x 3/2 dx
Solución:
∫ x -3/2 dx = x -3/2 + 1 /(-3/2 +1) + Constante
= x -1/2 /(-1/2) + C
= -2/(√x)+ C
(v) ∫ 3 x dx
Solución:
∫ 3 x dx = 3 x /log3 + constante
(vi) ∫ 1/x 2/3 dx
Solución:
∫ 1/x 2/3 dx = ∫ x -2/3 dx
= x -2/3 + 1 /(-2/3+1) + Constante
= x 1/3 /(1/3) + C
= 3x 1/3 + C
(vii) ∫ 3 2log 3 x dx
Solución:
∫ 3 2log 3 x dx =
= ∫ x 2 dx
= x 2+1 /(2+1) + constante
= x 3 /3 + C
Pregunta 2. Evaluar
(i) 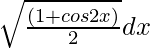
Solución:
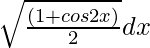
=
Sabemos, cos 2x = 2 cos 2 x – 1
=
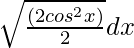
= ∫ cos x dx
= sen x + constante
(ii)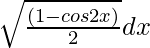
Solución:
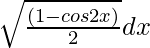
=
Sabemos, cos 2x = 1 – 2sen 2 x
=
= ∫ sen x dx
= -cos x + constante
Pregunta 3. Evaluar 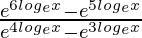
Solución:
dx
=
Sabemos, e log e x = x
=
= ∫ x 2 dx
= x 2+1 /2+1 + constante
= x 3 /3 + C
Pregunta 4. Evaluar: 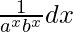
Solución:
= ∫ a -x b -x dx
= ∫ (ab) -x dx
= (ab) -x /log e (ab) -1 + Constante
= -a -x b -x /log e (ab) + C
o
= -a -x b -x / ln(ab) + C
Pregunta 5. Evaluar
(i) 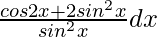
Solución:
=
Sabemos, cos x = 1 – 2sen 2 x
= ∫ 1/sen 2 x dx = ∫ cosec 2 x dx
= -cot x + constante
(ii) 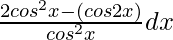
Solución:
Sabemos, cos x = 2 cos 2 x – 1
= ∫ 1/cos 2 x dx = ∫ segundo 2 x dx
= tan x + constante
Pregunta 6. Evalúa: ∫ e log√x /x dx
Solución:
∫ e log e √x /x dx = ∫√x/x dx
= ∫ x -1/2 dx = x -1/2 + 1 /(-1/2 + 1) + Constante
= x 1/2 /(1/2) + C
= 2√x + C
Publicación traducida automáticamente
Artículo escrito por ayushraghuwanshi80 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA