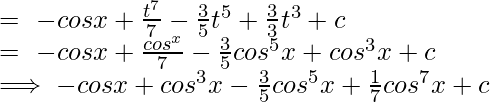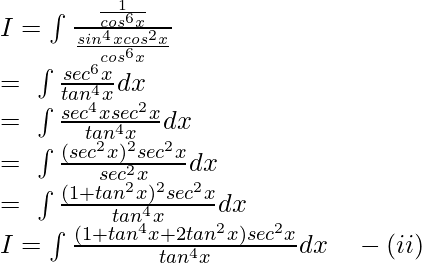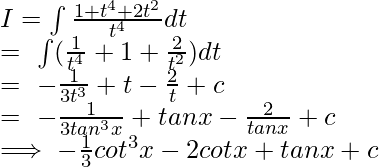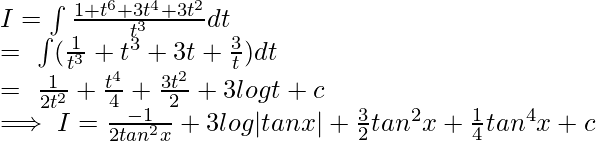Clase 12 Soluciones RD Sharma – Capítulo 19 Integrales indefinidas – Ejercicio 19.12

Pregunta 1. ∫sen ⁴ x cos ³ x dx

Solución:

Sea I = ∫ sen ⁴ x cos ³ x dx -(i)

Sea senx = t

Al derivar con respecto a x:

cosx = dt/dx

cosx dx = dt

dx = dt/cosx

Poniendo el valor de dx y senx en la ecuación (i):

yo = ∫ t ⁴ cos ^x dt/cosx
yo = ∫ t ⁴ cos ² x dt

yo = ∫ t ⁴ (1 – sen ² x) dt

yo = ∫ t ⁴ (1 – t ² ) dt

yo = ∫ (t ⁴ – t ² ) dt

yo = t ⁵ /5 – t ⁷ /7 + c

I = sen ^5/5 – sen ^7/7 + c

Pregunta 2. ∫ sen ⁵ x dx

Solución:

Sea I = ∫ sen ⁵ x dx

yo = ∫sen ³ xsen ² x dx

= ∫sen ³ x(1 – cos ² x)dx

= ∫(sen ³ x – sen ³ xcos ² x)dx

= ∫[senxsen ² x – sen ³ xcos ² x]dx

= ∫[senx(1 – cos ² x) – sen ³ xcos ² x]dx

= ∫(senx – senxcos ² x – sen ³ xcos ² x)dx

yo = ∫senx dx – ∫senxcos ² x dx – ∫sen ³ xcos ² x dx

Poniendo cosx = t y -sinxdx = dt en la 2da y 3ra integral:

yo = ∫senx dx + ∫t ² dt + ∫sen ² xt ³ dt/t

= ∫senx dx + ∫t ² dt + ∫sen ² xt ² dt

= ∫senx dx + ∫t ² dt + ∫(1 – cos ² x)t ² dt

$= -cosx+ \frac{t^3}{3} + \int (1-t^2)t^2dt\\ = -cosx + \frac{t^3}{3} + \int(t^2-t^4)dt\\ -cosx+\frac{t^3}{3}+\frac{t^3}{3}-\frac{t^5}{5}\\ -cosx+\frac{2t^3}{3}+\frac{t^5}{5}+c$ Poniendo valor de t: $\\ I=-cosx+\frac{2cos^3}{3}+\frac{cos^5}{5}+c$

Pregunta 3. ∫cos ⁵ x dx

Solución:

Sea I = ∫cos ⁵ x dx

yo = ∫ cos ² x cos ³ x dx

= ∫(1 – sen ² x)cos ³ x dx

= ∫(cos ³ x−sen ² xcos ³ x)dx

= ∫(cos ² xcosx – sen ² xcos ² xcosx)dx

= ∫[(1 – sen ² x)cosx – sen ² x(1 – sen ² x)cosx]dx

= ∫(cosx – sen ² xcosx – sen ² xcosx + sen ⁴ xcosx)dx

= ∫cosx dx – 2∫sen ² xcosx dx + ∫sen ⁴ xcosx dx

Poniendo senx = t y cosxdx = dt en la 2da y 3ra integral obtenemos:

yo = ∫cos dx – 2∫t ² dt + ∫t ⁴ dt

= senx – 2t ³ /3 + t ⁵ /5 + c

Poniendo valor de t:

I = = sen x – 2 sen ³ x/3 + cos ⁵ x/5 + c

Pregunta 4. ∫sen ⁵ xcosx dx

Solución:

Sea I = ∫sen ⁵ xcosx dx −(i)

Sea senx = t:

Al derivar con respecto a x:

-cosx = dt/dx

cosx dx = -dt

Poniendo cosxdx = -dt y senx = t en la ecuación (i):

yo = ∫t ⁵ dt

= t ⁶ /6 + c

= sen ⁶ x/6 + c

Pregunta 5. ∫sen ³ xcos ⁶ x dx

Solución:

Sea I = ∫sen ³ xcos ⁶ x dx −(i)

Sea cosx = t

Al diferenciar ambos lados wrt′x′:

-senx = dt/dx

senxdx = -dt

Poniendo cosx = t y sinxdx = -dt en la ecuación (i):

yo = -∫sen ² x t ⁶ dt

= -∫(1 – cos ² x)t ⁶ dt

= -∫(1 – t ² )t ⁶ dt

= -∫(t ⁶ – t ⁸ )dt

= -(t ⁷ /7 – t ⁹ /9) + c

Poniendo valor de t:

I = -(cos ⁷ x/7 – cos ⁹ x/9) + c

Pregunta 6. ∫cos ⁷ x dx

Solución:

Sea I = ∫cos ⁷ x dx

= ∫cos ⁶ xcosx dx

= ∫(cos ² x) ³ cosx dx

= ∫(1 – sen ² x) ³ cosx dx

= ∫(1 – sen ⁶ x – 3 sen ² x + 3 sen ⁴ x)cosx dx

= ∫(cosx – sen ⁶ xcosx – 3sen ² xcosx + 3sen ⁴ xcosx)dx −(i)

Poniendo senx = t y cosx dx = t en la 2da, 3ra y 4ta integral en (i):

yo = ∫cosx dx – ∫t ⁶ dt – 3∫t ² dt + 3∫t ⁴ dt

= senx – t ⁷ /7 - 3t ³ /3 +3t ⁵ /5 + c

Poniendo valor de t:

= sen x – sen ⁷ x/7 - 3 sen ³ x/3 +3 sen ⁵ x/5 + c

Pregunta 7. ∫xcos ³ x ² senx ² dx

Solución:

Sea I = ∫xcos ³ x ² senx ² dx −(i)

Sea cosx ² = t

Al diferenciar ambos lados:

-2xsenx ² = dt/dx

xsenx ² dx = -dt/2

Poniendo valores en (i):

$I=\int t^3\frac{-dt}{2}\\$

= -t ⁴ /8 + c

Poniendo valor de t:

$I=-\frac{1}{8}cos^4x^2+c$

Pregunta 8. ∫sen ⁷ x dx

Solución:

Sea I = ∫sen ⁷ x dx

yo = ∫sen ⁶ x senx dx

= ∫(sen ² x) ³ senx dx

= ∫(1 – cos ² x) ³ senx dx

= ∫(1 – cos ⁶ x – 3cos ² x + 3cos ⁴ x)senx dx

I = ∫senx dx – ∫cos ⁶ xsenx dx + 3∫cos ⁴ xsenx dx – 3∫cos ² xsenx dx

Poniendo cosx = t y senx dx = -dt en la 2da, 3ra y 4ta integral:

yo = ∫senx dx – ∫t ⁶ (-dt) + 3∫t ⁴ (-dt) – 3∫t ² (-dt)

$=\ -cosx+\frac{t^7}{7}-\frac{3}{5}t^5+\frac{3}{3}t^3+c\\ =\ -cosx+\frac{cos^x}{7}-\frac{3}{5}cos^5x+cos^3x+c\\ \implies -cosx+cos^3x-\frac{3}{5}cos^5x+\frac{1}{7}cos^7x+c$

Pregunta 9. ∫sen ³ xcos ⁵ x dx

Solución:

Sea I = ∫sen ³ xcos ⁵ x dx −(i)

Sea cosx = t

Al diferenciar ambos lados: -senx = dt/dx

sen x dx = -dt

Poniendo valores en (i):

yo = ∫sen ² xt ⁵ (-dt)

= ⁻ ∫(1 – cos ² x)t ⁵ dt

= ⁻ ∫(1 – t ² )t ⁵ dt

= ∫(t ⁷ – t ⁵ ) dt

= t ⁸ /8 – t ⁶ /6 + c

Poniendo valor de t:

$\implies \frac{1}{8}cos^8x-\frac{1}{6}cos^6x+c$

Pregunta 10. 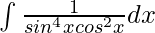$\int \frac{1}{sin^4xcos^2x}dx$

Solución:

Sea yo = $\int \frac{1}{sin^4xcos^2x}dx\quad -(i)$

Dividiendo y multiplicando la ecuación por cos ⁶ x:

$I=\int \frac{\frac{1}{cos^6x}}{\frac{sin^4xcos^2x}{cos^6x}}\\ =\ \int \frac{sec^6x}{tan^4x}dx\\ =\ \int \frac{sec^4xsec^2x}{tan^4x}dx\\ =\ \int \frac{(sec^2x)^2sec^2x}{sec^2x}dx\\ =\ \int \frac{(1+tan^2x)^2sec^2x}{tan^4x}dx\\ I=\int \frac{(1+tan^4x+2tan^2x)sec^2x}{tan^4x}dx\quad -(ii)\\$

Sea tanx = t, entonces:

seg ² x = dt/dx

segundo ² x dx = dt

Poniendo valores en la ecuación (ii):

$\\ I=\int \frac{1+t^4+2t^2}{t^4}dt\\ =\ \int (\frac{1}{t^4}+1+\frac{2}{t^2})dt\\ =\ -\frac{1}{3t^3}+t-\frac{2}{t}+c\\ =\ -\frac{1}{3tan^3x}+tanx-\frac{2}{tanx}+c\\ \implies -\frac{1}{3}cot^3x-2cotx+tanx+c$

Pregunta 11. 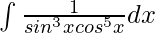$\int \frac{1}{sin^3xcos^5x}dx$

Solución:

$Let\ I=\int \frac{1}{sin^3xcos^5x}dx$ Dividiendo y multiplicando por cos ⁸ x: $\\ =\ \int \frac{\frac{1}{cos^8x}}{\frac{sin^3xcos^5x}{cos^8x}}dx\\ =\ \int \frac{sec^8x}{tan^3x}dx\\ =\ \int \frac{(sec^2x)^3}{tan^3x}sec^2xdx\\ =\ \int \frac{(1+tan^2x)^3}{tan^3x}sec^2xdx\\ =\ \int \frac{(1+tan^6x+3tan^2x+3tan^4x)sec^2x}{tan^3x}dx$ Sea tanx=t,entonces: $\\ sec^2x=\frac{dt}{dx}\\ \implies sec^2xdx=dt$ Poniendo valores en ii: $\\ I=\int \frac{1+t^6+3t^4+3t^2}{t^3}dt\\ =\ \int (\frac{1}{t^3}+t^3+3t+\frac{3}{t})dt\\ =\ \frac{1}{2t^2}+\frac{t^4}{4}+\frac{3t^2}{2}+3logt+c\\ \implies I=\frac{-1}{2tan^2x}+3log|tanx|+\frac{3}{2}tan^2x+\frac{1}{4}tan^4x+c$

Pregunta 12. 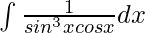$\int \frac{1}{sin^3xcosx}dx$

Solución:

$Let\ I=\int \frac{1}{sin^3xcosx}dx$ Dividiendo y multiplicando por cos ⁴ x: $\\ I=\int \frac{\frac{1}{cos^4x}}{\frac{sin^3xcosx}{cos^4x}}dx\\ I=\int \frac{sec^4x}{tan^3x}dx\\ I=\int \frac{sec^2xsec^2x}{tan^3x}dx\\ =\ \int \frac{1+tan^2x}{tan^3x}dx \quad -i$ Sea tanx=t,entonces: sec ² xdx = dt Poniendo valores en i: $\\ I=\int \frac{1+t^2}{t^3}dt\\ I=\int (\frac{1}{t^3}+\frac{1}{t})dt\\ =\ -\frac{1}{2t^2}+log|t|+c$ Poniendo valor de t: $\\ \implies -\frac{1}{2tan^2x}+log|tanx|+c$

Pregunta 13. 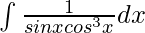$\int \frac{1}{sinxcos^3x}dx$

Solución:

$Let\ I=\int \frac{1}{sinxcos^3x}dx\\ \frac{1}{sinxcos^3x}= \frac{sin^2x+cos^2x}{sinxcos^3x}\\ =\ \frac{sinx}{cos^2x}+\frac{1}{sinxcosx}\\ =\ tanxsec^2x+\frac{\frac{1}{cos^2x}}{\frac{sinxcosx}{cos^2x}}\\ =\ tanxsec^2x+\frac{sec^2x}{tanx} \implies \int \frac{1}{sinxcos^3x}dx= \int tanxsec^2xdx +\int \frac{sec^2x}{tanx}dx$ Sea tanx=t⟹sec ² x dx = dt: $I= \int tdt+\int \frac{1}{t}dt\\ =\ \frac{t^2}{2}+log|t|+c$ Poniendo el valor de t: $\implies I=\frac{1}{2}tan^2x+log|tanx|+c$

Publicación traducida automáticamente

Artículo escrito por 07yuvraj y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. ∫sen 4 x cos 3 x dx

Pregunta 2. ∫ sen 5 x dx

Pregunta 3. ∫cos 5 x dx

Pregunta 4. ∫sen 5 xcosx dx

Pregunta 5. ∫sen 3 xcos 6 x dx

Pregunta 6. ∫cos 7 x dx

Pregunta 7. ∫xcos 3 x 2 senx 2 dx

Pregunta 8. ∫sen 7 x dx

Pregunta 9. ∫sen 3 xcos 5 x dx

Pregunta 10.

Pregunta 11.

Pregunta 12.

Pregunta 13.

Deja una respuesta Cancelar la respuesta

Pregunta 1. ∫sen ⁴ x cos ³ x dx

Pregunta 2. ∫ sen ⁵ x dx

Pregunta 3. ∫cos ⁵ x dx

Pregunta 4. ∫sen ⁵ xcosx dx

Pregunta 5. ∫sen ³ xcos ⁶ x dx

Pregunta 6. ∫cos ⁷ x dx

Pregunta 7. ∫xcos ³ x ² senx ² dx

Pregunta 8. ∫sen ⁷ x dx

Pregunta 9. ∫sen ³ xcos ⁵ x dx

Pregunta 10. $\int \frac{1}{sin^4xcos^2x}dx$

Pregunta 11. $\int \frac{1}{sin^3xcos^5x}dx$

Pregunta 12. $\int \frac{1}{sin^3xcosx}dx$

Pregunta 13. $\int \frac{1}{sinxcos^3x}dx$