Pregunta 25. Evalúa ∫(tanx + cotx) 2 dx
Solución:
∫(bronceadox + cunax) 2 dx
Usando la fórmula (x + y) 2 = x 2 + y 2 + 2xy
Obtenemos, ∫(tan 2 x + cot 2 x + 2tanx cotx)dx
= ∫ (seg 2 x – 1 + cosec 2 x – 1 + ((2 × 1)/cotx) × cotx)dx
= ∫ (seg 2 x + cosec 2 x)dx
= ∫seg 2 xdx + ∫coseg 2 xdx
= bronceadox – cunax + c
Pregunta 26. Evalúa ∫(1 – cos2x)/(1 + cos2x) dx
Solución:
∫(1 – cos2x)/(1 + cos2x) dx
= ∫(2sen 2 x)/(2cos 2 x) dx
= ∫tan 2 xdx
= ∫(seg 2 x – 1)dx
= ∫seg 2 xdx – 1∫dx
= tanx – x + c
Pregunta 27. Evalúa ∫(cosx)/(1 – cosx) dx
Solución:
∫(cosx)/(1 – cosx) dx
= ∫(cosx(1 + cosx))/((1 – cosx)(1 + cosx)) dx
= ∫(cosx + cos 2 x)/(1 – cos 2 x) dx
= ∫(cosx + cos 2 x)/(sen 2 x) dx
= ∫(cosx)/(sen 2 x) dx + ∫(cos 2 x)/(sen 2 x) dx [Ya que, cosx/senx = cotx]
= ∫cotx × cosecxdx + ∫(cosec 2 x – 1)dx [Ya que, cot 2 x = cosec 2 x – 1]
= -cosecx – cotx – x + c
Pregunta 28. Evalúa ∫cos 2 x – sen 2 x/√(1 + cos4x) dx
Solución:
∫cos 2 x – sen 2 x/√(1 + cos4x) dx
= ∫(cos 2 x – sen 2 x)/√(2cos 2 2x) dx
= 1/√2 ∫(cos 2 x – sen 2 x)/(cos 2x) dx
= 1/√2∣(cos 2 x – sen 2 x)/(cos 2 x – sen 2 x) dx
= 1/√2∫1 × dx
= x/√2 + c
Pregunta 29. Evalúa ∫ 1/(1 – cosx) dx
Solución:
Tenemos, ∫ 1/(1 – cosx) dx
= ∫1/(1 – cosx) × (1 + cosx)/(1 + cosx) × dx
= ∫(1 + cosx)/(1 – cos 2x ) × dx
= ∫(1 + cosx)/(sen 2 x) × dx
= ∫1/(sen 2 x) dx + ∫(cosx)/(sen 2 2x) dx
= ∫coseg 2 xdx + ∫cotx × cosecx dx
= -cotx – cosecx + c
Pregunta 30. Evalúa ∫1/(1 – sinx) dx
Solución:
Tenemos, ∫1/(1 – senx) dx
= ∫1/(1 – senx) × (1 + senx)/(1 + senx) × dx
= ∫(1 + senx)/(1 – sen 2 x) × dx
= ∫(1 + senx)/(cos 2 x) × dx
= ∫(1/(cos 2 x) + (senx)/(cos 2 x)) × dx
= ∫1/(cos 2 x) dx + ∫(senx)/(cos 2 x) × dx
= ∫sec 2 xdx + ∫tanx secx dx
= tanx + secx + c
Pregunta 31. Evalúa ∫(tanx)/(secx + tanx) dx
Solución:
Tenemos, ∫(tanx)/(secx + tanx) dx
= ∫(tanx)/(secx + tanx) × (secx – tanx)/(secx – tanx) × dx
= ∫(tanx(segx – tanx))/(seg 2 x – tan 2 x) × dx
= ∫(tanxsecx – tan 2 x)dx
= ∫segtanxdx – ∫(seg 2 x – 1)dx
= ∫segxtanxdx – ∫seg 2 xdx + 1∫dx
= secx – tanx + x + c
Pregunta 32. Evalúa ∫(cosecx)/(cosecx – cotx)dx
Solución:
Tenemos, ∫(cosecx)/(cosecx – cotx)dx
= ∫(cosecx)/(cosecx – cotx) × (cosecx + cotx)/(cosecx + cotx) × dx
= ∫(cosecx(cosecx + cotx))/(cosec 2 x – cot 2 x) × dx
= ∫(cosec 2 x + cosecx cotx)dx
= ∫cosec 2 xdx + ∫cosecx cotx dx
= -cotx – cosecx + c
Pregunta 33. Evalúa ∫1/(1 + cos2x) dx
Solución:
Tenemos, ∫1/(1 + cos2x) dx
= ∫ 1/(2cos 2 x) × dx
= 1/2 ∫seg 2 x × dx
= 1/2 × tanx + c
= (tanx)/2 + c
Pregunta 34. Evalúa∫1/(1 – cos2x) dx
Solución:
Tenemos, ∫1/(1 – cos2x) dx
= ∫1/(2sen 2 x)dx
= 1/2 ∫coseg 2 x dx
= (-1)/2 × cunax + c
= (-cotx)/2 + c
Pregunta 35. Evalúa ∫tan -1 [(sin2x)/(1 + cos2x)]dx
Solución:
Tenemos, ∫tan -1 [(sin2x)/(1 + cos2x)]dx
= ∫tan -1 [(2senxcosx)/(2cos 2 x)]dx
= ∫tan -1 [(senx)/(cosx)]dx
= ∫tan -1 (tanx)dx
= ∫xdx
= x 2 /2 + c
Pregunta 36. Evalúa ∫cos -1 (sinx)dx
Solución:
Tenemos, ∫cos -1 (senx)dx
= ∫cos -1 [cos(π/2 – x)]dx
= ∫(π/2 – x)dx
= π/2 ∫dx – ∫xdx
= π/2 × x – x 2 /2 + c
Pregunta 37. Evalúa ∫ cot -1 (sinx)dx
Solución:
Tenemos, ∫ cot -1 (sinx)dx
= ∫cot -1 [(sen2x)/(1 – cos2x)]dx
= ∫cot -1 ((cosx)/(senx))dx
= ∫cot -1 (cotx)dx
= ∫xdx
= x 2 /2 + c
Pregunta 38. Evalúa ∫ sen -1 ((2tanx)/(1 + tan 2 x))dx
Solución:
Tenemos, ∫ sen -1 ((2tanx)/(1 + tan 2 x))dx
= ∫ sin -1 (sin2x)dx
= ∫2xdx
= 2∫xdx
= (2x 2 )/2 + c
= x 2 + c
Pregunta 39. Evalúa ∫((x 3 + 8)(x – 1))/(x 2 – 2x + 4) dx
Solución:
Tenemos, ∫((x 3 + 8)(x – 1))/(x 2 – 2x + 4) dx
= ∫((x + 2)(x 2 – 2x + 4)(x – 1))/(x 2 – 2x + 4) dx
= ∫(x + 2)(x – 1)dx
= ∫(x 2 – x+2x – 2)dx
= ∫(x2 + x – 2 )dx
= x3 / 3 + x2 / 2 – 2x + c
Pregunta 40. Evalúa ∫(atanx + bcotx) 2 dx
Solución:
Tenemos, ∫(atanx + bcotx) 2 dx
Usando la fórmula (x + y) 2 = x 2 + y 2 + 2xy , obtenemos
= ∫(a 2 tan 2 x + b 2 cot 2 x + 2ab tanx cotx)dx
= ∫[a 2 (seg 2 x – 1) + b 2 (coseg 2 x – 1) + 2ab]dx
= ∫[a 2 seg 2 x – a 2 + b 2 cosec 2 x – b 2 + 2ab]dx
= a 2 tanx – a 2 x – b 2 cotx – b 2 x + 2abx + c
= a 2 tanx – b 2 cotx – (a 2 + b 2 – 2ab)x + c
Pregunta 41. Evalúa ∫(x 3 – 3x 2 + 5x – 7 + x 2 a x )/(2x 2 ) dx
Solución:
Tenemos, ∫(x 3 – 3x 2 + 5x – 7 + x 2 a x )/(2x 2 ) dx
= 1/2 ∫x 3 /x 2 dx – 3/2∫x 2 /x 2 dx + 5/2∫x/x 2 dx – 7/2∫x -2 dx + 1/2∫(x 2 a x )/x 2 dx
= 1/2 × x 2 /2 – 3/2x + 5/2 logx – 7/2 x -1 + 1/2a x /(loga) + c
= 1/2 [x 2 /2 – 3x + 5logx + 7/x + a x /(loga)] + c
Pregunta 42. Evalúa ∫cosx/(1 + cosx) dx
Solución:
Tenemos, ∫cosx/(1 + cosx) dx …..(1)
ahora resuelve
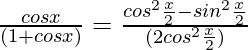
Ya que, cosx = cos 2 x/2 – sen 2 x/2 y cosx + 1 = 2cos 2 x/2
Entonces, obtenemos cosx/(1 + cosx) = 1/2[1 – tan 2 x/2]
Ahora ponga este valor en la ecuación (1), obtenemos
= 1/2 ∫(1 – tan 2 x/2)dx
= 1/2 ∫(1 – segundo 2 x/2 + 1)dx
= 1/2 ∫(2 – seg 2 x/2)dx
= 1/2 [2x – (tanx/2)/(1/2)] + c
= x – tanx/2 + c
Pregunta 43. Evalúa∫(1 – cosx)/(1 + cosx) dx
Solución:
Tenemos, ∫(1 – cosx)/(1 + cosx) dx ….(1)
ahora resuelve
(1 – cosx)/(1 + cosx) = (2sen 2 x)/(2cos 2 x)
= bronceado 2 x/2
= (seg 2 x/2 – 1) [Ya que, 2sen 2 x/2 = 1 – cosx y 2cos 2 x/2 = 1 + cosx]
Ahora ponga este valor en la ecuación (1), obtenemos
= ∫(seg 2 x/2 – 1)dx
= tan(x/2)/(1/2) – x + c
= 2tanx/2 – x + c
Pregunta 44. Evalúa ∫{3sinx – 4cosx + 5/(cos 2 x) – 6/(sen 2 x) + tan 2 x – cot 2 x}dx
Solución:
Tenemos, ∫{3sinx – 4cosx + 5/(cos 2 x) – 6/(sen 2 x) + tan 2 x – cot 2 x}dx
= 3∫senxdx – 4∫cosxdx + 5∫sec 2 dx – 6∫cosec 2 x + ∫tan 2 xdx – ∫cot 2 xdx
= 3∫senxdx – 4∫cosxdx + 5∫sec 2 xdx – 6∫cosec 2 x + ∫(sec 2 x – 1)dx – ∫(cosec 2 x – 1)dx
= 3∫sinxdx – 4∫cosxdx + 6∫seg 2 xdx – 7∫coseg 2 xdx
= -3cosx – 4senx + 6tanx + 7cotx + c
Pregunta 45. Si f'(x) = x – 1/x 2 y f(1) = 1/2, encuentre f(x)?
Solución:
Dado que ∫f'(x) = x – 1/x 2
yf(1) = 1/2
Tenemos que encontrar f(x)
Entonces, ∫f'(x) = ∫xdx – ∫1/x 2 dx
f(x) = x2 / 2 + x- 1 + c
f(x) = x2 / 2 + 1/x + c
f(x) = x 2 /2 + 1/x + c …..(i)
Como sabemos que
f(1) = 1/2
1 2 /2 + 1/1 + c = 1/2
1/2 + 1 + c = 1/2
c = -1
Al poner c = -1 en (i), obtenemos
f(x) = x2 / 2 + 1/x – 1
Pregunta 46. Si f'(x) = x + b, f(1) = 5, f(2) = 13, encuentre f(x)?
Solución:
Dado que f'(x) = x + b
y f(1) = 5, f(2) = 13
Tenemos que encontrar f(x)
Entonces, ∫f'(x) = ∫(x + b)dx
f(x) = x 2 /2 + bx + c …….(i)
Como sabemos que
f(1) = 5
1 2 /2 + segundo × 1 + do = 5
1/2 + b + c = 5
b + c = 9/2 …….(ii)
Además, f(2) = 13
2 2 /2 + b × 2 + c = 13
2 + 2b + c = 13
2b + c = 11 …….(iii)
Ahora, restando eq(ii) de eq(iii), obtenemos
b = 11 – 9/2
b = 13/2
Ahora, pon b = 13/2 en la ecuación (ii), obtenemos
13/2 + c = 9/2
c = 9/2 – 13/2
c = (9 – 13)/2
= (-4)/2
= -2
Ahora, al poner b = 13/2 y c = -2 en la ecuación (i), obtenemos
f(x) = x2 /x + 13/2x – 2
f(x) = x2 / 2 + 13/2x – 2
Pregunta 47. Si f'(x) = 8x 3 – 2x, f(2) = 8, encuentre f(x)?
Solución:
Dado que f'(x) = 8x 3 – 2x
yf(2) = 8
Tenemos que encontrar f(x)
Entonces, ∫f'(x)dx = ∫(8x 3 – 2x)dx
f(x) = ∫(8x 3 – 2x)dx
= ∫8x 3 dx – ∫2xdx
= (8x 4 )/4 – (2x 2 )/2 + c
= 2x 4 – x 2 + c
f(x) = 2x 4 – x 2 + c ……….(i)
Como sabemos que f(2) = 8
Entonces, f(2) = 2(2) 4 – (2) 2 + c = 8
32 – 4 + c = 8
28 + c = 8
c = -20
Ahora, pon c = -20 en la ecuación (i), obtenemos
f(x) = 2x 4 – x 2 – 20
Pregunta 48. Si f'(x) = asinx + bcosx y f'(0) = 4, f(0) = 3, f(π/2) = 5, encuentra f(x)?
Solución:
Dado que, f'(x) = asinx + bcosx
y f'(0) = 4, f(0) = 3, f(π/2) = 5
Tenemos que encontrar f(x)
Asi que,
∫f'(x) = ∫(asenx + bcosx)dx
f(x) = -acosx + bsenx + c
f(x) = -acosx + bsenx + c ………(i)
Como sabemos que f'(0) = 4
Entonces, f'(0) = asen0 + bcos0 = 4
un × 0 + segundo × 1 = 4
segundo = 4
Además, f(0) = 3
f(0) = -acos0 + bsen0 + c = 3
-a + 0 + c = 3
c – a = 3 ……..(ii)
Además, f(π/2) = 5
f(π/2) = -acos(π/2) + bsen(π/2) + c = 5
-a × 0 + b × 1 + c = 5
b + c = 5
4 + c = 5 [Ya que, b = 4]
do = 5 – 4
c = 1
Ahora, pon c = 1 en la ecuación (ii), obtenemos 1 – a = 3
-a = 3 – 1
-a = 2
un = -2
Ahora, ponga a = -2, b = 4 y c = 1 en la ecuación (i), obtenemos
f(x) = -(-2)cosx + 4sinx + 1
f(x) = 2cosx + 4senx + 1
Pregunta 49. Escribe la primitiva o antiderivada de f(x) = √x + 1/√x.
Solución:
Tenemos, f(x) = √x + 1/√x
∫f(x) = ∫(√x + 1/√x)dx
= ∫x 1/2 dx + ∫ x -1/2 dx
= 2/3 x 3/2 + 2x 1/2 + c
Por tanto, la primitiva o antiderivada de f(x) es 2/3 x 3/2 + 2x 1/2 + c.
Publicación traducida automáticamente
Artículo escrito por anandchaturvedirishra y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA