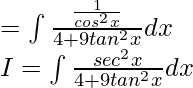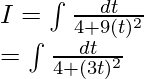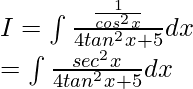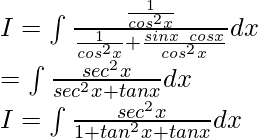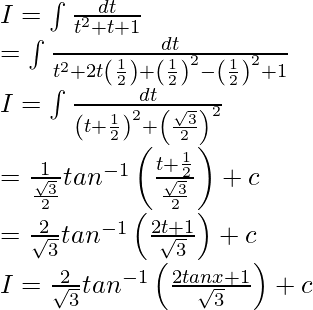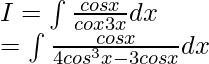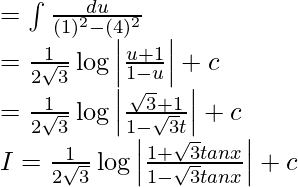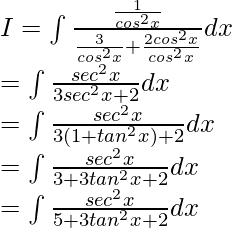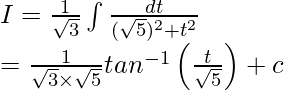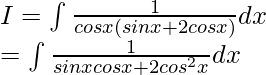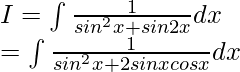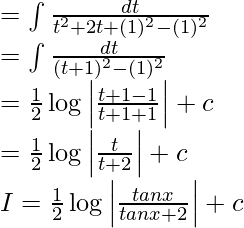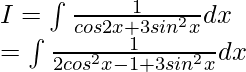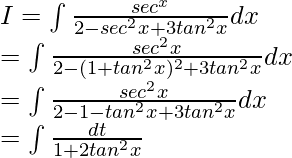Clase 12 Soluciones RD Sharma – Capítulo 19 Integrales indefinidas – Ejercicio 19.22

Pregunta 1. Evalúa la integral:

$\int\frac{1}{4cos^2x+9sin^2x}dx$

Solución:

Dejar $I=\int\frac{1}{4cos^2x+9sin^2x}dx$

Al dividir numerador y denominador entre cos ² x, obtenemos

$=\int\frac{\frac{1}{cos^2x}}{4+9tan^2x}dx\\ I=\int\frac{sec^2x}{4+9tan^2x}dx\\$

Consideremos tan x = t

Entonces, sec ² x dx = dt

$I=\int\frac{dt}{4+9(t)^2}\\ =\int\frac{dt}{4+(3t)^2}$

De nuevo, consideremos 3t = u

3dt = du

$I=\frac{1}{3}\int\frac{du}{(2)^2+(u)^2}$

= (3/2) × (1/2) × bronceado ^-1 (u/2) + c

= (1/6)tan ^-1 (3t/2) + c

Por lo tanto, I = (1/6)tan ^-1 (3tanx/2) + c

Pregunta 2. Evalúa la integral:

$\int\frac{1}{4sin^2x+5cos^2x}dx$

Solución:

Dejar $I=\int\frac{1}{4sin^2x+5cos^2x}dx$

Al dividir numerador y denominador entre cos ² x, obtenemos

$I=\int\frac{\frac{1}{cos^2x}}{4tan^2x+5}dx\\ =\int\frac{sec^2x}{4tan^2x+5}dx$

Ahora, consideremos tan x = t

Entonces, seg ² xdx = dt

$I=\int\frac{dt}{4+9(t)^2}\\ =\int\frac{dt}{4t^2+5}$

De nuevo, consideremos 2t = u

2dt = du

$I=\frac{1}{2}\int\frac{du}{(4)^2+(\sqrt{5})^2}$

= (1/2) × (1/√5) × bronceado ^-1 (u/√5) + c

= (1/2√5) × bronceado ^-1 (2t/√5) + c

Por lo tanto, yo = (1/2√5) × tan ^-1 (2tanx/√5) + c

Pregunta 3. Evalúa la integral:

$\int\frac{2}{2+sin2x}dx$

Solución:

Dejar $I=\int\frac{2}{2+sin2x}dx\\ =\int\frac{2}{2+2sinx\ cosx}dx$

Al dividir numerador y denominador entre cos ² x, obtenemos

$I=\int\frac{\frac{1}{cos^2x}}{\frac{1}{cos^2x}+\frac{sinx\ cosx}{cos^2x}}dx\\ =\int\frac{sec^2x}{sec^2x+tanx}dx\\ I=\int\frac{sec^2x}{1+tan^2x+tanx}dx$

Ahora, consideremos tan x = t

Entonces, sec ² x dx = dt

$I=\int\frac{dt}{t^2+t+1}\\ =\int\frac{dt}{t^2+2t\left(\frac{1}{2}\right)+\left(\frac{1}{2}\right)^2-\left(\frac{1}{2}\right)^2+1}\\ I=\int\frac{dt}{\left(t+\frac{1}{2}\right)^2+\left(\frac{\sqrt3}{2}\right)^2}\\ =\frac{1}{\frac{\sqrt3}{2}}tan^{-1}\left(\frac{t+\frac{1}{2}}{\frac{\sqrt3}{2}}\right)+c\\ =\frac{2}{\sqrt3}tan^{-1}\left(\frac{2t+1}{\sqrt3}\right)+c\\ I=\frac{2}{\sqrt{3}}tan^{-1}\left(\frac{2tanx+1}{\sqrt3}\right)+c$

Pregunta 4. Evalúa la integral:

$\int\frac{cosx}{cos3x}dx$

Solución:

Dejar $I=\int\frac{cosx}{cox3x}dx\\ =\int\frac{cosx}{4cos^3x-3cosx}dx$

Al dividir numerador y denominador entre cos ² x, obtenemos

$I=\int\frac{\frac{cosx}{cos^3x}}{\frac{4cos^3x}{cos^3x}+\frac{3cosx}{cos^3x}}dx\\ =\int\frac{sec^2x}{4-3sec^2x}dx\\ =\int\frac{sec^2x}{4-3(1+tan^2x)}dx\\ =\int\frac{sec^2x}{4-3-3tan^2x}dx\\ =\int\frac{sec^2x}{1-3tan^2x}dx$

Ahora, consideremos tan x = t

Entonces, sec ² x dx = dt

$I=\int\frac{dt}{1-3t^2}\\ =\int\frac{dt}{1-(\sqrt3t)^2}$

De nuevo, consideremos √3t = u

Entonces, √3dt = du

$=\int\frac{du}{(1)^2-(4)^2}\\ =\frac{1}{2\sqrt3}\log\left|\frac{u+1}{1-u}\right|+c\\ =\frac{1}{2\sqrt3}\log\left|\frac{\sqrt3+1}{1-\sqrt3t}\right|+c\\ I=\frac{1}{2\sqrt3}\log\left|\frac{1+\sqrt3tanx}{1-\sqrt3tanx}\right|+c$

Pregunta 5. Evalúa la integral:

$\int\frac{1}{1+3sin^2x}dx$

Solución:

Dejar $I=\int\frac{1}{1+3sin^2x}dx$

Al dividir numerador y denominador entre cos ² x, obtenemos

$I=\int\frac{\frac{1}{cos^2x}}{\frac{1}{cos^2x}+\frac{3sin^2x}{cos^2x}}dx\\ =\int\frac{sec^2x}{sec^2x+3tan^2x}dx\\ =\int\frac{sec^2x}{1+tan^2x+3tan^2x}dx\\ =\int\frac{sec^2x}{1+\{2tanx\}^2}dx\\ =\int\frac{sec^x}{1+\{2tanx\}^2}dx$

Ahora, supongamos 2tan x = t

Entonces, 2 seg ² x dx = dt

yo = 1/2 ∫dt/(1 + t ² )

= 1/2 tan ^-1 t + c

Por lo tanto, I = 1/2 tan ^-1 (2tanx) + c

Pregunta 6. Evalúa la integral:

$\int\frac{1}{3+2cos^2x}dx$

Solución:

Dejar $I=\int\frac{1}{3+2cos^2x}dx$

Al dividir numerador y denominador entre cos ² x, obtenemos

$I=\int\frac{\frac{1}{cos^2x}}{\frac{3}{cos^2x}+\frac{2cos^2x}{cos^2x}}dx\\ =\int\frac{sec^2x}{3sec^2x+2}dx\\ =\int\frac{sec^2x}{3(1+tan^2x)+2}dx\\ =\int\frac{sec^2x}{3+3tan^2x+2}dx\\ =\int\frac{sec^2x}{5+3tan^2x+2}dx$

Ahora, supongamos √3 tanx = t

Entonces, √3 seg ² x dx = dt

$I=\frac{1}{\sqrt3}\int\frac{dt}{(\sqrt5)^2+t^2}\\ =\frac{1}{\sqrt3\times\sqrt5}tan^{-1}\left(\frac{t}{\sqrt5}\right)+c\\$

Por lo tanto, I = (1/√15)tan ^-1 (√3tanx/√5) + c

Pregunta 7. Evalúa la integral:

$\int\frac{1}{(sinx-2cosx)(2sinx+cosx)}dx$

Solución:

Dejar $I=\int\frac{1}{(sinx-2cosx)(2sinx+cosx)}dx\\ =\int\frac{1}{2sin^2x+sinxcosx-4sinxcosx-2cos^2x}dx\\ =\int\frac{1}{2sin^2x-3sinxcosx-2cos^2x}dx$

Al dividir numerador y denominador entre cos ² x, obtenemos

$I=\int\frac{sec^2x}{2tan^2x-3tanx-2}dx$

Ahora, supongamos que tanx = t

Entonces, sec ² x dx = dt

$I=\int\frac{dt}{2t^2-3t-2}\\ =\frac{1}{2}\int\frac{dt}{t^2-\frac{3}{2}t-1}\\ =\frac{1}{2}\int\frac{dt}{t^2-2t\left(\frac{3}{4}\right)+\left(\frac{3}{4}\right)^2-\left(\frac{3}{4}\right)^2-1}\\ I=\frac{1}{2}\int\frac{dt}{\left(t-\frac{3}{4}\right)^2-\left(\frac{5}{4}\right)^2}\\ =\frac{1}{2}\times\frac{1}{2\frac{5}{4}}\log\left|\frac{t-\frac{3}{4}-\frac{5}{4}}{t-\frac{3}{4}+\frac{5}{4}}\right|+c\\ =\frac{1}{5}\log\left|\frac{t-2}{2t+1}\right|+c\\ I=\frac{1}{5}\log\left|\frac{tanx-2}{2tanx+1}\right|+c$

Pregunta 8. Evalúa la integral:

$\int\frac{sin2x}{sin^4x+cos^4x}dx$

Solución:

Dejar $I=\int\frac{sin2x}{sin^4x+cos^4x}dx$

Al dividir numerador y denominador entre cos ⁴ x, obtenemos

$I=\int\frac{2tan^2x sec^2x}{tan^4x+1}$

Ahora, supongamos tan ² x = t

Entonces, 2tanx seg ² x dx = dt

yo = ∫dt/(t ² + 1)

= bronceado ^-1 t + c

I = tan ^-1 (tan ² x) + c

Pregunta 9. Evalúa la integral:

$\int\frac{1}{cosx(sinx+2cosx)}dx$

Solución:

Dejar $I=\int\frac{1}{cosx(sinx+2cosx)}dx\\ =\int\frac{1}{sinxcosx+2cos^2x}dx$

Al dividir numerador y denominador entre cos ² x, obtenemos

$I=\int\frac{sec^2x}{tanx + 2}dx$

Ahora, supongamos 2 + tanx = t

Entonces, sec ² x dx = dt

yo = ∫dt/t

= registro|t| +c

I = log|2 + tanx| +c

Pregunta 10. Evalúa la integral:

$\int\frac{1}{sin^2x+sin2x}dx$

Solución:

Dejar $I=\int\frac{1}{sin^2x+sin2x}dx\\ =\int\frac{1}{sin^2x+2sinxcosx}dx$

Al dividir numerador y denominador entre cos ² x, obtenemos

$I=\int\frac{sec^2x}{tan^2x+2tanx}dx$

Ahora, supongamos que tanx = t

Entonces, sec ² x dx = dt

$=\int\frac{dt}{t^2+2t+(1)^2-(1)^2}\\ =\int\frac{dt}{(t+1)^2-(1)^2}\\ =\frac{1}{2}\log\left|\frac{t+1-1}{t+1+1}\right|+c\\ =\frac{1}{2}\log\left|\frac{t}{t+2}\right|+c\\ I=\frac{1}{2}\log\left|\frac{tanx}{tanx+2}\right|+c$

Pregunta 11. Evalúa la integral:

$\int\frac{1}{cos2x+3sin^2x}dx$

Solución:

Dejar $I=\int\frac{1}{cos2x+3sin^2x}dx\\ =\int\frac{1}{2cos^2x-1+3sin^2x}dx$

Al dividir numerador y denominador entre cos ² x, obtenemos

$I=\int\frac{sec^x}{2-sec^2x+3tan^2x}dx\\ =\int\frac{sec^2x}{2-(1+tan^2x)^2+3tan^2x}dx\\ =\int\frac{sec^2x}{2-1-tan^2x+3tan^2x}dx\\ =\int\frac{dt}{1+2tan^2x}$

Ahora, supongamos √2tanx = t

Entonces, √2seg ² dx = dt

yo = 1/√2 ∫1/(1 + t ² )

= 1/√2 tan ^-1 t + c

Por lo tanto, I = 1/√2 tan ^-1 (√2tanx) + c

Publicación traducida automáticamente

Artículo escrito por sudhasinghsudha90 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Evalúa la integral:

Pregunta 2. Evalúa la integral:

Pregunta 3. Evalúa la integral:

Pregunta 4. Evalúa la integral:

Pregunta 5. Evalúa la integral:

Pregunta 6. Evalúa la integral:

Pregunta 7. Evalúa la integral:

Pregunta 8. Evalúa la integral:

Pregunta 9. Evalúa la integral:

Pregunta 10. Evalúa la integral:

Pregunta 11. Evalúa la integral:

Deja una respuesta Cancelar la respuesta