Clase 12 Soluciones RD Sharma – Capítulo 19 Integrales indefinidas – Ejercicio 19.25 | Serie 1

Evalúa las siguientes integrales:

Pregunta 1. ∫x cos⁡xdx

Solución:

Dado que, I = ∫x cos⁡xdx

Usando la integración por partes,       

∫uv dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c 

Obtenemos

yo = x∫cos⁡xdx – ∫(1 × ∫cos⁡xdx)dx + c

= xsen⁡x – ∫sen⁡xdx + c

Por lo tanto, yo = x sen⁡x + cos⁡x + c

Pregunta 2. ∫log⁡(x + 1)dx

Solución:

Dado que, I = ∫log⁡(x + 1)dx

= ∫1 × log⁡(x + 1)dx

Usando la integración por partes,       

∫uv dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c 

Obtenemos

yo = log⁡(x + 1)∫1dx – ∫(1/(x + 1) × ∫ 1dx)dx + c

= xlog⁡(x + 1) – ∫(x/(x + 1))dx + c

= x log⁡(x + 1) – ∫(1 – 1/(x + 1))dx + c

Por lo tanto, yo = x log⁡(x + 1) – x + log⁡(x + 1) + c

Pregunta 3. ∫x ³ log⁡xdx

Solución:

Dado que, I = ∫ x ³ log⁡xdx

Usando la integración por partes,       

∫uv dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c 

Obtenemos

yo = log⁡x ∫x ³ dx – ∫(1/x × ∫x ³ dx)dx + c

= x ⁴ /4 log⁡x – ∫x ⁴ /4x dx+c

= x ⁴ /4 log⁡x – 1/4∫x ³ dx + c

= x ⁴ /4 log⁡x – 1/4 ∫x ⁴ /4 dx + c

yo = x ⁴ /4 log⁡x – 1/16 x ⁴ + c

Pregunta 4. ∫xe ^x dx

Solución:

Dado que I = ∫xe ^x dx

Usando la integración por partes,       

∫uv dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c 

Obtenemos

yo = xe ^x – ∫1.e ^x dx

= xe ^x – e ^x + c

Por lo tanto, yo = = xe ^x – e ^x + c

Pregunta 5. ∫xe ^2x dx

Solución:

Dado que, I = ∫xe ^2x dx

Usando la integración por partes,       

∫uv dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c 

Obtenemos

yo = x∫e ^2x dx – ∫(1 × ∫ e ^2x dx) dx + c

= x∫e ^2x dx – ∫(1 × ∫e ^2x dx)dx + c

= (xe ^2x )/2 – ∫(e ^2x /2)dx + c

= (xe ^2x )/2 – e ^2x /4 + c

Por lo tanto, yo = (x/2 – 1/4) e ^2x + c

Pregunta 6. ∫x ² e ^-x dx

Solución:

Dado que I = ∫x ² e ^-x dx

Usando la integración por partes,       

∫uv dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c 

Obtenemos

yo = x ² ∫e ^-x dx – ∫(2x∫e ^-x dx)dx

= -x ² e ^-x – ∫(2x)(-e ^-x )dx

= -x ² e ^-x + 2∫xe ^-x dx

= -x ² e ^-x + 2[x∫e ^-x dx – ∫(1 × ∫ e ^-x dx) dx]

= -x ² e ^-x + 2[x(-e ^-x ) – ∫(-e ^-x )dx]

= -x ² e ^-x – 2xe ^-x + 2∫e ^-x dx

Por lo tanto, yo = -x ² e ^-x – 2xe ^-x – 2e ^-x + c

Pregunta 7. ∫ x ² cos⁡xdx

Solución:

Dado que, I = ∫ x ² cos⁡xdx

Usando la integración por partes,       

∫uv dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c 

Obtenemos

 yo = x ² ∫ cos⁡xdx – ∫(2x)cos⁡xdx)dx

= x ² sen⁡x – 2∫(x)(sen⁡x)dx

= x ² sin⁡x – 2[x∫sin⁡xdx – ∫(1 × ∫sin⁡xdx)dx]

= x ² sen⁡x – 2[x(-cos⁡x) – ∫(-cos⁡x)dx]

= x ² sen⁡x + 2xcos⁡x – 2∫(cos⁡x)dx

Por lo tanto, yo = x ² sin⁡x + 2xcos⁡x – 2sin⁡x + c

Pregunta 8. ∫x ² cos⁡2xdx

Solución:

Dado que, I = ∫x ² cos⁡2xdx

Usando la integración por partes,       

∫uv dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c 

Obtenemos

yo = x ² ∫cos⁡2xdx – ∫(2x∫ cos⁡2xdx)dx

= x ² (sen⁡2x)/2 – 2∫x((sen⁡2x)/2)dx

= 1/2 x ² sen⁡2x – ∫xsen⁡2xdx

= 1/2 x ² sin⁡2x – [x∫sin⁡2xdx – ∫ (1∫ sin⁡2xdx)dx]

= 1/2 x ² sen⁡2x – [x((-cos⁡2x)/2) – ∫(-(cos⁡2x)/2)dx]

= 1/2 x ² sen⁡2x + x/2 cos⁡2x – 1/2 ∫(cos⁡2x)dx

Por lo tanto, I = 1/2 x ² sen⁡2x + x/2 cos⁡2x – 1/4 sen⁡2x + c

Pregunta 9. ∫xsen⁡2xdx

Solución:

Dado que, I =∫xsen⁡2xdx

Usando la integración por partes,       

∫uv dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c 

Obtenemos

 yo = x∫sin⁡2xdx – ∫(1)sin⁡2xdx)dx

= x(-(cos⁡2x)/2) – ∫(-(cos⁡2x)/2)dx

= -x/2 cos⁡2x + 1/2 ∫cos⁡2xdx

= -x/2 cos⁡2x + 1/2(sen⁡2x)/2 + c

Por lo tanto, yo = -x/2 cos⁡2x + 1/4 sen⁡2x + c

Pregunta 10. ∫(log⁡(log⁡x))/x dx

Solución:

 Dado que,I = ∫(log⁡(log⁡x))/x dx 

= ∫(1/x)(log⁡(log⁡x))dx

Usando la integración por partes,       

∫uv dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c 

Obtenemos

yo = log⁡log⁡x]1/x dx – ∫(1/(xlog⁡x)∫1/x dx)dx

= log⁡x × log⁡(log⁡x) – ∫(1/(xlog⁡x) log⁡x)dx

= log⁡x × log⁡(log⁡x) – ∫1/x dx

= log⁡x × log⁡(log⁡x) – log⁡x + c

Por lo tanto, yo = log⁡x(log⁡log⁡x – 1) + c

Pregunta 11. ∫x ² cos⁡xdx

Solución:

Dado que I = ∫x ² cos⁡xdx

Usando la integración por partes,       

∫uv dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c 

Obtenemos

yo = x ² ∫ cos⁡xdx – ∫(2x]cos⁡xdx)dx

= x ² sen⁡x – 2∫xsen⁡xdx

= x ² sin⁡x – 2[x∫sin⁡xdx – ∫(1]sin⁡xdx)dx]

= x ² sen⁡x – 2[x(-cos⁡x) – ∫(-cos⁡x)dx]

= x ² sen⁡x + 2xcos⁡x – 2∫(cos⁡x)dx

Por lo tanto, yo = x ² sin⁡x + 2xcos⁡x – 2sin⁡x + c

Pregunta 12. ∫xcosec ² ⁡xdx

Solución :

Dado que, I = ∫xcosec ² ⁡xdx

Usando la integración por partes,       

∫uv dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c 

Obtenemos

I = x∫coseg ² xdx – ∫(∫ cosec ² xdx)dx

= -xcot⁡x + ∫cot⁡xdx

= -x cot⁡x + log ⁡|sin⁡x| +c

Por lo tanto, yo = -x cot⁡x + log ⁡|sin⁡x| +c

Pregunta 13. ∫xcos ² xdx

Solución:

Dado que, I = ∫xcos ² xdx

Usando la integración por partes,       

∫uv dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c 

Obtenemos

yo = x∫ cos ² ⁡xdx – ∫(1∫ cos ² xdx)dx

= x∫((cos⁡2x + 1)/2)dx – ∫(∫((1 + cos⁡2x)/2)dx)dx

= x/2 [(sen⁡2x)/2 + x] – 1/2∫(x + (sen⁡2x)/2)dx

= x/4 sen⁡2x + x ² /2 – 1/2 × x ² /2 – 1/4 (-(cos⁡2x)/2) + c

Por lo tanto, I = x/4 sen⁡2x + x ² /4 + 1/8 cos⁡2x + c

Pregunta 14. ∫x ⁿ log⁡x dx

Solución:

Dado que, I = ∫x ⁿ log⁡xdx

Usando la integración por partes,       

∫uv dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c 

Obtenemos

yo = log⁡x∫x norte ^dx – ∫(1/x ∫x norte ^dx )dx

= x ⁿ⁺¹ /(n + 1) log⁡x – ∫(1/x × x ⁿ⁺¹ /(n + 1))dx

= x ⁿ⁺¹ /(n + 1) log⁡x – ∫(x ⁿ /(n + 1))dx

Por lo tanto, yo = x ⁿ⁺¹ /(n + 1) log⁡x – 1/(n + 1) ² × (x ⁿ⁺¹ ) + c

Pregunta 15. ∫(log⁡x)/x ⁿ dx

Solución:

Dado que, I = ∫(log⁡x)/x ⁿ dx = ∫(log⁡x)(1/x ⁿ )dx

Usando la integración por partes,       

∫uv dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c 

Obtenemos

yo = log⁡x∫(1/x ⁿ )dx – ∫((d(log⁡x))/dx)(∫(1/x ⁿ )dx)dx

= log⁡x(x ^1-n /(1 – n)) – ∫1/x (x ^1-n /(1 – n))dx

= log⁡x(x ^1-n /(1 – n)) – ∫(x ⁿ /(1 – n))dx

= log⁡x(x ^1-n /(1 – n)) – (1/(1 – n))(x ^1-n /(1 – n))

Por lo tanto, yo = log⁡x(x ^1-n /(1 – n)) – (x ^1-n /([1 – n] ² )) + c

Pregunta 16. ∫x ² sen ² ⁡xdx

Solución:

Dado que, I = ∫x ² sen ² ⁡xdx

= ∫x ² ((1 – cos⁡2x)/2)dx

Usando la integración por partes,       

∫uv dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c 

Obtenemos

= ∫x ² /2 dx – ∫((x ² cos⁡2x)/2)dx

= x ³ /6 – 1/2 [∫x ² cos⁡2xdx]

= x ³ /6 – 1/2 [x ² ∫cos⁡2xdx – ∫ (2x∫cos⁡2xdx)dx]

= x ³ /6 – 1/2 (x ² (sen⁡2x)/2) + 1/2 × 2∫(x (sen⁡2x)/2)dx

= x ³ /6 – 1/4 x ² sin⁡2x + 1/2 [x ∫sin⁡2xdx – ∫(1∫sin⁡2xdx)dx]

= x ³ /6 – 1/4 x ² sin⁡2x + 1/2 [x(-(cos⁡2x)/2) – ∫(-(cos⁡2x)/2)dx] 

= x ³ /6 – 1/4 x ² sen⁡2x + 1/2 x(-(cos⁡2x)/2) + 1/4 × (sen2x/2) + c

= x ³ /6 – 1/4 x ² sen⁡2x – 1/4 x(cos⁡2x) + 1/8 × (sen2x) + c

Por lo tanto, I = x ³ /6 – 1/4 x ² sin⁡2x – 1/4 x(cos⁡2x) + 1/8 × (sin2x) + c

Pregunta 17.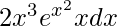 

Solución:

Dado que, l = 

 Supongamos, x ² = t

2xdx = dt

yo = ∫t × e ^t dt

Usando la integración por partes,       

∫uv dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c 

Obtenemos

= t∫e ^t dt – ∫(1 × ∫e ^t dt)dt

= te ^t – ∫e ^t dt

= te ^t – e ^t + c

= e ^t-1 + c

Por lo tanto, yo =   (x ² – 1) + c

Pregunta 18. ∫x ³ cos⁡x ² dx

Solución:

Dado que, I = ∫x ³ cos⁡x ² dx

Supongamos que x ² = t

2xdx = dt

yo = 1/2 ∫tcos⁡tdt

Usando la integración por partes,       

∫uv dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c 

Obtenemos

= 1/2[t∫cos⁡tdt – ∫(1 × ∫cos⁡tdt)dt]

= 1/2 [t × sin⁡t – ∫sin⁡tdt]

= 1/2[tsin⁡t + costo⁡t] + c

Por lo tanto, yo = 1/2 [x² sen⁡x ² + cos⁡x ² ] + c

Pregunta 19. ∫xsen⁡xcos⁡xdx

Solución:

Dado que, I = ∫xsen⁡xcos⁡xdx

 = ∫x/2(2sen⁡xcos⁡x)dx

 = 1/2 ∫xsen⁡2xdx

Usando la integración por partes,       

∫uv dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c 

Obtenemos

= 1/2 [x∫sin⁡2xdx – ∫(1 × ∫sin⁡2xdx)dx]

= 1/2 [x((-cos⁡2x)/2) – ∫((-cos⁡2x)/2)dx]

= -1/4 xcos⁡2x + 1/4 ∫cos⁡2xdx

Por lo tanto, yo = -1/4 xcos⁡2x + 1/8 sin⁡2x + c

Pregunta 20. ∫sen⁡x(log⁡cos⁡x)dx

Solución:

Dado que, I = ∫sin⁡x(log⁡cos⁡x)dx

 Consideremos, cos⁡x = t

 -sin⁡xdx = dt

yo = -∫ log⁡tdt

 = -∫1 × log⁡tdt

Usando la integración por partes,       

∫uv dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c 

Obtenemos

= -[log⁡t∫dt – ∫(1/t × ∫dt)dt]

= -[tlog⁡t – ∫1/t × tdt]

= -[tlog⁡t-∫ dt]

= -[tlog⁡t – t + c ₁ ]

= t(1 – logaritmo) + c

Por lo tanto, I = cosx(1 – logcosx) + c