Pregunta 1. ∫e ax cosbx dx
Solución:
Tenemos,
yo = ∫e hacha cosbx dx
Usando la integración por partes, obtenemos,
I = e hacha (senbx)/b − a∫e hacha (senbx)/b dx
I = e hacha (senbx)/b − (a/b)[−e hacha (cosbx)/b + a∫e hacha (cosbx)/b dx]
yo = e hacha (senbx)/b + (a/b 2 ) e hacha (cosbx) − (a 2 /b 2 )∫e hacha (cosbx) dx
I = (e ax /b 2 ) [b senbx + a cos bx] + (a 2 /b 2 ) I + c
(a 2 +b 2 )I/b 2 = (e ax /b 2 ) [b senbx + a cos bx] + c
Por tanto, I = e ax [b senbx + a cos bx]/(a 2 +b 2 ) + c
Pregunta 2. ∫e ax sen(bx+c)dx
Solución:
Tenemos,
I = ∫e ax sen(bx+c)dx
Usando la integración por partes, obtenemos,
I = − e ax cos(bx+c)/b + ∫ae ax cos(bx+c)/b dx
I = (−1/b) e ax cos(bx+c) + (a/b) ∫e ax cos(bx+c) dx
I = (−1/b) e ax cos(bx+c) + (a/b) [e ax sin(bx+c)/b − ∫ae ax sin(bx+c)/b dx]
I = (−1/b) e ax cos(bx+c) + (a/b 2 ) e ax sin(bx+c) − (a 2 /b 2 )∫e ax sin(bx+c) dx
yo = (e hacha /b 2 ) [a sen(bx+c) − b cos(bx+c)] − (a 2 /b 2 ) yo + c
(a 2 +b 2 ) I/b 2 = (e hacha /b 2 ) [a sin(bx+c) − b cos(bx+c)] + c
Por lo tanto, I = (e ax )[a sin(bx+c)−b cos(bx+c)]/(a 2 +b 2 ) + c
Pregunta 3. ∫cos(logx) dx
Solución:
Tenemos,
yo = ∫cos(logx) dx
Sea log x = t, entonces obtenemos, (1/x)dx = dt
=> dx = xdt
=> dx = e t dt
Entonces, la ecuación se convierte en,
yo = ∫e t costo dt
Usando la integración por partes, obtenemos,
yo = mi t sint − ∫e t sint dt
yo = e t sint − [−e t costo + ∫e t costo dt]
yo = e t sint + e t costo − yo + c
2I = e t (sint+coste) + c
I = e t (sint+coste)/2 + c
Por tanto, yo = x[cos(logx) + sin(logx)]/2 + c
Pregunta 4. ∫e 2x cos(3x+4)dx
Solución:
Tenemos,
yo = ∫e 2x cos(3x+4)dx
Usando la integración por partes, obtenemos,
yo = e 2x sen(3x+4)/3 − ∫2e 2x sen(3x+4)/3 dx
yo = (1/3) e 2x sen(3x+4) − (2/3) ∫e 2x sen(3x+4) dx
I = (1/3) e 2x sin(3x+4) − (2/3) [−e 2x cos(3x+4)/3 + ∫2e 2x cos(3x+4)/3 dx]
I = (1/3) e 2x sen(3x+4) + (2/9) e 2x cos(3x+4) − (4/9)∫2e 2x cos(3x+4) dx]
yo = (e 2x /9) [2 cos(3x+4)−3 sen(3x+4)] − (4/9)yo + c
(13/9)I = (e 2x /9) [2 cos(3x+4)−3 sen(3x+4)] + c
Por tanto, I = e 2x [2 cos(3x+4)−3 sin(3x+4)]/13 + c
Pregunta 5. ∫e 2x senx cosx dx
Solución:
Tenemos,
yo = ∫e 2x senx cosx dx
yo = (1/2)∫e 2x (2senx cosx) dx
yo = (1/2)∫e 2x sen2x dx
Usando la integración por partes, obtenemos,
yo = (1/2)[−e 2x (cos2x)/2 + ∫2e 2x (cos2x)/2 dx]
2I = −e 2x (cos2x)/2 + ∫e 2x (cos2x)dx
2I = −e 2x (cos2x)/2 + [e 2x (sen2x)/2 − ∫2e 2x (sen2x)/2 dx]
2I = −e 2x (cos2x)/2 + e 2x (sen2x)/2 − 2I + c
4I = e 2x (sen2x−cos2x)/2 + c
Por lo tanto, I = e 2x (sen2x−cos2x)/8 + c
Pregunta 6. ∫e 2x senx dx
Solución:
Tenemos,
yo = ∫e 2x senx dx
Usando la integración por partes, obtenemos,
yo = e 2x (−cosx) + ∫2e 2x cosx dx
yo = −e 2x cosx + 2[e 2x senx − 2∫e 2x senx dx]
yo = −e 2x cosx + 2e 2x senx − 4∫e 2x senx dx
yo = e 2x (2senx−cosx) − 4I + c
5I = e 2x (2senx−cosx) + c
Por lo tanto, I = e 2x (2senx−cosx)/5 + c
Pregunta 7. ∫e 2x sen(3x+1) dx
Solución:
Tenemos,
yo = ∫e 2x sin(3x+1) dx
Usando la integración por partes, obtenemos,
yo = −e 2x cos(3x+1)/3 + ∫2e 2x cos(3x+1)/3 dx
I = −(1/3) e 2x cos(3x+1) + (2/3) [e 2x sin(3x+1)/3 − ∫2e 2x sin(3x+1)/3 dx]
I = −(1/3) e 2x cos(3x+1) + (2/3) [e 2x sin(3x+1)/3 − (2/3)∫e 2x sin(3x+1)dx]
yo = −(1/3) e 2x cos(3x+1) + (2/9) e 2x sen(3x+1) − (4/9)yo + c
(13/9)I = e 2x [2sen(3x+1)−3cos(3x+1)]/9 + c
Por lo tanto, I = e 2x [2sin(3x+1)−3cos(3x+1)]/13 + c
Pregunta 8. ∫e x sen 2 x dx
Solución:
Tenemos,
yo = ∫e x sen 2 x dx
yo = (1/2)∫e x (1−cos2x)dx
yo = (1/2)∫e x dx − (1/2)∫e x cos2x dx
Sea I 1 = ∫e x cos2x dx. Entonces, nuestra ecuación se convierte en,
yo = (1/2)∫e X dx − (1/2) yo 1 . . . . (1)
Usando integración por partes en I 1 , obtenemos,
yo 1 = e x (sen2x)/2 − ∫e x (sen2x)/2 dx
I 1 = e x (sen2x)/2 − (1/2)[−e x (cos2x)/2 + ∫e x (cos2x)/2 dx
yo 1 = e x (sen2x)/2 + e x (cos2x)/4 − (1/4)∫e x cos2x dx
yo 1 = e x [2sen2x+cos2x)]/4 − (1/4) yo 1
(5/4)I 1 = e x [2sen2x+cos2x)]/4
I 1 = e x [2sen2x+cos2x)]/5 . . . . (2)
Poniendo (2) en (1), obtenemos,
yo = (1/2)∫e x − (1/2) (1/5) e x [2sin2x+cos2x)] + c
Por lo tanto, I = e x /2 − e x [2sen2x+cos2x)]/10 + c
Pregunta 9. ∫(1/x 3 ) sin(logx) dx
Solución:
Tenemos,
yo = ∫(1/x 3 ) sen(logx) dx
Sea logx = t, entonces tenemos, (1/x)dx = dt
=> dx = xdt
=> dx = e t dt
Entonces, la ecuación se convierte en,
yo = ∫(1/e 3t ) (sint) e t dt
yo = ∫e −2t sint dt
Usando la integración por partes, obtenemos,
I = −e −2t costo − ∫2e −2t costo dt
I = −e −2t coste − 2[e −2t sint + ∫2e −2t sint ]
I = −e −2t coste − 2e −2t sint − 4∫e −2t sint
I = −e −2t [coste+2sint] − 4I + c
5I = −e −2t [coste+2sint] + c
I = −e −2t [coste+2sint]/5 + c
yo = −e −2logx [cos(logx)+2sin(logx)]/5 + c
I = −x -2 [coste+2sint]/5 + c
Por lo tanto, I = −[coste+2sint]/5x 2 + c
Pregunta 10. ∫e 2x cos 2 x dx
Solución:
Tenemos,
yo = ∫e 2x cos 2 x dx
yo = (1/2) ∫e 2x (1+cos2x) dx
yo = (1/2) ∫e 2x dx + (1/2) ∫e 2x cos2x dx
Sea I1 = ∫e 2x cos2x dx. Entonces, nuestra ecuación se convierte en,
yo = (1/2)∫e 2x dx + (1/2) yo 1 . . . . (1)
Usando integración por partes en I 1 , obtenemos,
yo 1 = e 2x (sen2x)/2 − ∫2e 2x (sen2x)/2 dx
yo 1 = e 2x (sen2x)/2 − ∫e 2x sen2x dx
I 1 = e 2x (sen2x)/2 − [−e 2x (cos2x)/2 + ∫2e 2x (cos2x)/2 dx]
yo 1 = e 2x (sen2x)/2 + e 2x (cos2x)/2 − ∫e 2x (cos2x) dx
yo 1 = e 2x (sen2x+cos2x)/2 − yo 1
2I 1 = e 2x (sen2x+cos2x)/2
yo 1 = e 2x (sen2x+cos2x)/4 . . . . (2)
Poniendo (2) en (1), obtenemos,
yo = (1/2)∫e 2x dx + (1/2) (1/4) [e 2x (sen2x+cos2x)]
Por tanto, yo = (1/4) e 2x + (1/8) [e 2x (sen2x+cos2x)] + c
Pregunta 11. ∫e −2x senx dx
Solución:
Tenemos,
yo = ∫e −2x senx dx
Integrando por partes, obtenemos,
yo = −e −2x cosx − ∫2e −2x cosx dx
yo = −e −2x cosx − 2[e −2x senx+∫2e −2x senx dx]
yo = −e −2x cosx − 2e −2x senx − 4∫e −2x senx dx
yo = −e −2x (cosx+2senx) − 4I + c
5I = −e −2x (cosx+2senx) + c
Por lo tanto, yo = −e −2x (cosx+2senx)/5 + c
Pregunta 12. 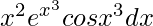
Solución:
Tenemos,
yo =
Sea x 3 = t, entonces tenemos, 3x 2 dx = dt
Entonces, la ecuación se convierte en,
yo = (1/3) ∫e t costo dt
Integrando por partes, obtenemos,
yo = (1/3) [e t sint − ∫e t sint dt]
I = (1/3) [e t sint − (−e t costo + ∫e t costo dt)]
I = (1/3) e t sint + (1/3) e t costo − (1/3) ∫e t costo dt
I = e t [sint+cost]/3 − I + c
2I = e t [sint+coste]/3 + c
I = e t [sint+cost]/6 + c
Por lo tanto, yo =
Publicación traducida automáticamente
Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA