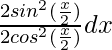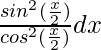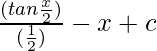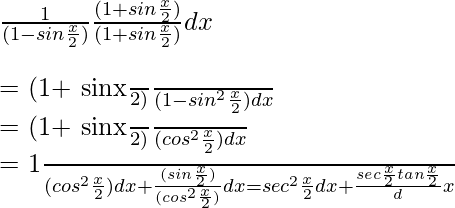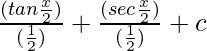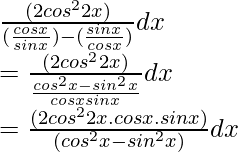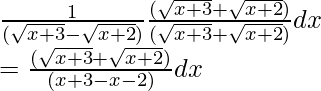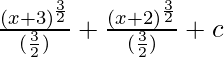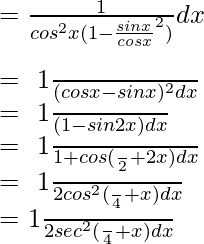Clase 12 Soluciones RD Sharma – Capítulo 19 Integrales indefinidas – Ejercicio 19.3

Pregunta 11. Integrar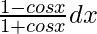 $∫\frac{1-cosx}{1+cosx}dx$

Solución:

Sea yo = $∫\frac{1-cosx}{1+cosx}dx$

Al simplificar la ecuación anterior, obtenemos

yo = $∫\frac{2 sin^2(\frac{x}{2})}{2 cos^2(\frac{x}{2})} dx$

= $∫\frac{sin^2 (\frac{x}{2})}{cos^2 (\frac{x}{2})} dx$

= ∫ tan ² x/2 dx

= $∫(sec^2\frac{x}{2} - 1) dx -(1)$

Al integrar la ecuación (1), obtenemos

= $\frac{(tan \frac{x}{2})}{(\frac{1}{2})} - x +c$

Por lo tanto, I = 2 tan x/2 – x + c

Pregunta 12. Integrar 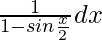$∫ \frac{1}{1-sin\frac{x}{2}} dx$

Solución:

Sea yo = $∫ \frac{1}{1-sin\frac{x}{2}} dx$

Ahora multiplica con el conjugado,

= $∫ \frac{1}{(1-sin\frac{x}{2})} × \frac{(1 + sin \frac{x}{2})}{(1+ sin \frac{x}{2})} dx\\ = ∫\frac{(1+ sin\frac{x}{2})}{(1- sin^2 \frac{x}{2})} dx\\ = ∫\frac{(1+ sin\frac{x}{2})}{(cos^2 \frac{x}{2})} dx\\ = ∫\frac{1}{(cos^2\frac{x}{2})} dx + ∫\frac{(sin \frac{x}{2})}{(cos^2\frac{x}{2})} dx\\= ∫ sec^2 \frac{x}{2} dx + ∫ \frac{sec \frac{x}{2} tan \frac{x}{2}} dx$

Al integrar la ecuación, obtenemos

= $\frac{(tan \frac{x}{2})}{(\frac{1}{2})} + \frac{(sec \frac{x}{2})}{(\frac{1}{2})} + c$

= 2 tan x/2 + 2 seg x/2 +c

Por tanto, I = 2 (tan x/2 + sec x/2) + c

Pregunta 13. Integrar 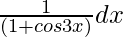$∫ \frac{1}{(1 + cos 3x)} dx$

Solución:

Sea yo = $∫ \frac{1}{(1 + cos 3x)} dx$

Ahora multiplica con el conjugado,

= ∫ 1/(1 + cos 3x) × (1 – cos 3x)/(1 – cos 3x) dx

= ∫ (1 – cos 3x)/ (1 – cos ² 3x) dx

= ∫ (1 – cos 3x)/ (sen ² 3x) dx

= ∫ (1/ sen ² 3x) – (cos 3x/ sen ² 3x) dx

= ∫ (cosec ² 3x – cosec3x cot3x) dx -(1)

Al integrar la ecuación (1), obtenemos

= – cuna 3x/3 + cosec 3x/3 + c

= (-1/3) × (cos 3x/ sen 3x) + (1/3) × (1/sen 3x) + c

= (1 – cos 3x) / 3 sen 3x + c

Por tanto, I = (1 – cos 3x) / 3 sen 3x + c

Pregunta 14. Integra ∫(e ^x + 1) ² e ^x dx

Solución:

Sea I = ∫ (e ^x + 1) ² e ^x dx -(1)

(ex + 1) ⁼ t -(2)

Al diferenciar la ecuación anterior, obtenemos

e ^x dx = dt -(3)

Ahora, pon la ecuación (2) y (3) en la ecuación (1)

= ∫ (t ² ) dt -(4)

Al integrar la ecuación (4), obtenemos

= (t ³ /3) + c

Por lo tanto, yo = (ex ⁺ 1) ^3/3 + c

Pregunta 15. Integrar ∫ (e ^x + (1 + e ^x )) ² dx

Solución:

Sea I = ∫ (e ^x + (1/e ^x )) ² dx

= ∫ (e ^2x + (1/e ^2x ) + 2)dx -(1)

Al integrar la ecuación (1), obtenemos

= (e ^2x /2) – (1/2 e ^-2x ) + 2x + c

Por tanto, yo = (e ^2x /2) – (1/2 e ^-2x ) + 2x + c

Pregunta 16. Integrar 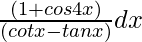$∫ \frac{(1 + cos 4x)}{(cot x - tan x)} dx$

Solución:

Sea yo = $∫ \frac{(1 + cos 4x)}{(cot x - tan x)} dx$

= $∫\frac{(2 cos^2 2x)}{(\frac{cos x}{sin x}) - (\frac{sin x}{cos x})} dx \\ = ∫ \frac{(2 cos^2 2x)}{\frac{cos^2x - sin^2x}{cosx sinx}} dx \\ = ∫ \frac{(2 cos^2 2x. cosx.sinx)}{(cos^2x - sin^2x)} dx$

Al simplificar la ecuación anterior,

= ∫ cos ² 2x. (sen2x / cos2x) dx

= ∫ cos 2x. sin2x dx

= 1/2∫ sen (2x + 2x) + sen (2x – 2x) dx

= 1/2∫(sen 4x + sen 0) dx

= 1/2∫(sen 4x + 0) dx

= 1/2 ∫sen 4x dx -(1)

Al integrar la ecuación (1), obtenemos

= (-1/2) ((cos 4x)/4) + c

Por tanto, yo = (-1/8) (cos 4x) + c

Pregunta 17. Integrar 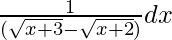$∫ \frac{1} {(\sqrt{x +3} - \sqrt{x + 2})} dx$

Solución:

Sea yo = $∫ \frac{1} {(\sqrt{x +3} - \sqrt{x + 2})} dx$

Ahora multiplica con el conjugado,

= $∫ \frac{1}{(\sqrt{x +3} - \sqrt{x + 2})} × \frac{(\sqrt{x +3} + \sqrt{x + 2})}{(\sqrt{x +3} + \sqrt{x + 2})} dx\\ = ∫\frac{(\sqrt{x +3} + \sqrt{x + 2})}{(x+3-x-2)} dx$

= ∫(x +3) ^1/2 + (x + 2) ^1/2 dx -(1)

Al integrar la ecuación (1), obtenemos

= $\frac{(x+3)^{\frac{3}{2}}}{(\frac{3}{2})} + \frac{(x+2)^{\frac{3}{2}}}{(\frac{3}{2})} + c$

= (2/3)(x + 3) ^3/2 +(2/3) (x + 2) ^3/2 + c

Por lo tanto, yo = (2/3){(x + 3) ^3/2 + (x + 2) ^3/2 } +c

Pregunta 18. Integra ∫ tan ² (2x – 3) dx

Solución:

Sea I = ∫ tan ² (2x – 3) dx

= ∫ seg ² (2x – 3) – 1 dx -(1)

Ahora pon, 2x – 3 = t -(2)

2dx = dt-(3)

Poner eq(3) y (2) en eq(1)

= 1/2∫seg ² t dt – ∫1dx -(4)

Al integrar la ecuación (4), obtenemos

= 1/2 tan t – x + c

= 1/2 tan(2x – 3) – x + c

Por lo tanto, yo = 1/2 tan(2x – 3) – x + c

Pregunta 19. Integrar 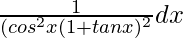$∫ \frac{1}{(cos^2x(1+tanx)^2} dx$

Solución:

Sea yo = $∫ \frac{1}{(cos^2x(1+tanx)^2} dx$

$= ∫ \frac{1}{cos^2x(1-\frac{sinx}{cosx}^2)} dx\\ = ∫ \frac{1}{(cosx - sinx)^2} dx\\ = ∫ \frac{1}{(1-sin2x)} dx\\ = ∫ \frac{1}{1+cos(\frac{π}{2} + 2x)} dx\\ = ∫ \frac{1}{2cos^2(\frac{π}{4} + x)} dx\\ = \frac{1}{2} ∫ sec^2(\frac{π}{4} + x) dx$

Al integrar la ecuación, obtenemos

= 1/2 tan(π/4 + x) + c

Por lo tanto, I = 1/2 tan(π/4 + x) + c

Publicación traducida automáticamente

Artículo escrito por yogirao y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 12 Soluciones RD Sharma – Capítulo 19 Integrales indefinidas – Ejercicio 19.3 | conjunto 2

Pregunta 11. Integrar $∫\frac{1-cosx}{1+cosx}dx$

Pregunta 12. Integrar $∫ \frac{1}{1-sin\frac{x}{2}} dx$

Pregunta 13. Integrar $∫ \frac{1}{(1 + cos 3x)} dx$

Pregunta 14. Integra ∫(e ^x + 1) ² e ^x dx

Pregunta 15. Integrar ∫ (e ^x + (1 + e ^x )) ² dx

Pregunta 16. Integrar $∫ \frac{(1 + cos 4x)}{(cot x - tan x)} dx$

Pregunta 17. Integrar $∫ \frac{1} {(\sqrt{x +3} - \sqrt{x + 2})} dx$

Pregunta 18. Integra ∫ tan ² (2x – 3) dx

Pregunta 19. Integrar $∫ \frac{1}{(cos^2x(1+tanx)^2} dx$

Deja una respuesta Cancelar la respuesta

Pregunta 11. Integrar

Pregunta 12. Integrar

Pregunta 13. Integrar

Pregunta 14. Integra ∫(e x + 1) 2 e x dx

Pregunta 15. Integrar ∫ (e x + (1 + e x )) 2 dx

Pregunta 16. Integrar

Pregunta 17. Integrar

Pregunta 18. Integra ∫ tan 2 (2x – 3) dx

Pregunta 19. Integrar

Deja una respuesta Cancelar la respuesta

Pregunta 11. Integrar $∫\frac{1-cosx}{1+cosx}dx$

Pregunta 12. Integrar $∫ \frac{1}{1-sin\frac{x}{2}} dx$

Pregunta 13. Integrar $∫ \frac{1}{(1 + cos 3x)} dx$

Pregunta 14. Integra ∫(e ^x + 1) ² e ^x dx

Pregunta 15. Integrar ∫ (e ^x + (1 + e ^x )) ² dx

Pregunta 16. Integrar $∫ \frac{(1 + cos 4x)}{(cot x - tan x)} dx$

Pregunta 17. Integrar $∫ \frac{1} {(\sqrt{x +3} - \sqrt{x + 2})} dx$

Pregunta 18. Integra ∫ tan ² (2x – 3) dx

Pregunta 19. Integrar $∫ \frac{1}{(cos^2x(1+tanx)^2} dx$