Pregunta 1. Integrar 
Solución:
Vamos, yo =
Usa el método de división, entonces obtenemos,
= ∫ (x + 3)dx – 4∫1/(x + 2) dx
Integrar la ecuación anterior, entonces obtenemos
= x 2 /2 + 3x – 4 log |x + 2| +c
Por lo tanto, I = x 2 /2 + 3x – 4 log |x + 2| +c
Pregunta 2. Integrar 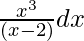
Solución:
Sea yo =
Usa el método de división, entonces obtenemos,
= ∫ x 2 dx + 2∫x dx + 4∫ dx + 8 ∫1/(x – 2) dx
Integrar la ecuación anterior, entonces obtenemos
= x 3 /3 + 2x 2 /2 + 4x + 8 log|x – 2| +c
= x 3 /3 + x 2 + 4x + 8 log|x – 2| +c
Por lo tanto, I = x 3 /3 + x 2 + 4x + 8 log|x – 2| +c
Pregunta 3. Integrar 
Solución:
Vamos, yo =
Usa el método de división, entonces obtenemos,
=
Integrar la ecuación anterior, entonces obtenemos
=
= x2 / 6 + x/9 + (43/27) log|3x + 2| +c
Por lo tanto, yo = = x 2 /6 + x/9 + (43/27) log|3x + 2| +c
Pregunta 4. Integrar 
Solución:
Vamos, yo =
Podemos escribir la ecuación anterior de la siguiente manera,
=
Al resolver la ecuación anterior,
=
=
= 2∫ (1/(x – 1) dx + 5 ∫(x – 1) -2 dx
Integrar la ecuación anterior, entonces obtenemos
= 2 log|x – 1| + 5 (x – 1) -1 /(-1) + c
= 2 log|x – 1| – 5 / (x – 1) + c
Por lo tanto, yo = 2 log|x – 1| – 5 / (x – 1) + c
Pregunta 5. Integrar 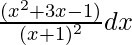
Solución:
Vamos, yo =
Podemos escribir la ecuación anterior de la siguiente manera,
=
=
=
=
= ∫ dx – ∫ 1/ (x + 1) dx + 2∫1/(x + 1) dx -3 ∫(x + 1) -2 dx
Integrar la ecuación anterior, entonces obtenemos
= x – registro|x + 1| + 2 log|x + 1| – 3(x + 1) -1 /(-1) + c
= x – registro|x + 1| + 2 log|x + 1| + 3/(x + 1) + c
= x + log|x + 1| + 3/(x + 1) + c
Por lo tanto, yo = x + log|x + 1| + 3/(x + 1) + c
Pregunta 6. Integrar 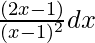
Solución:
Vamos, yo =
=
=
=
=
= 2∫ 1/(x – 1) dx + ∫(x – 1) -2 dx
Integrar la ecuación anterior, entonces obtenemos
= 2 log|x – 1| + (x – 1) -1 /(-1) + c
= 2 log|x – 1| – 1/(x – 1) + c
Por lo tanto, yo = 2 log|x – 1| – 1/(x – 1) + c