Pregunta 1. 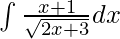
Solución:
Dada integral,
Al multiplicar y dividir por 2, obtenemos
⇒
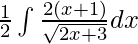
⇒
⇒
⇒
Usando la fórmula,
[donde c es cualquier constante arbitraria]
Obtenemos
⇒
⇒
⇒
⇒
![Rendered by QuickLaTeX.com \frac{1}{2}(2x+3)^\frac{1}{2}[\frac{2x+3}{3}-1]+c](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-980acb97105ac29fe988b66115df4b74_l3.png)
Pregunta 2. 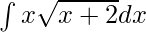
Solución:
Dada integral,
Sea x + 2 =t ⇒x = t – 2
Al diferenciar en ambos lados,
dx = dt
Al sustituirlo en la integral dada, obtenemos
⇒
⇒
Sabemos que,
[donde c es cualquier constante arbitraria]
⇒
⇒
Reemplazando x en términos de t
⇒
⇒
Pregunta 3. 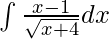
Solución:
Dada integral,
⇒
⇒
⇒
Usando la fórmula,
[donde c es cualquier constante arbitraria]
Obtenemos
⇒
⇒
⇒
Pregunta 4. 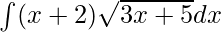
Solución:
Dada integral,
Sea 3x + 5 = t
⇒ x = (t – 5)/3
Al diferenciar ambos lados,
dx = dt/3
Al reemplazar los términos x por t,
⇒
⇒
⇒
Usando la fórmula,
[donde c es cualquier constante arbitraria]
Obtenemos
⇒
⇒
Al reemplazar t con x términos
⇒
⇒
⇒
Pregunta 5. 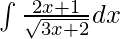
Solución:
Dada integral,
Al multiplicar y dividir por 3
⇒
⇒
⇒
⇒
Usando la fórmula,
[donde c es cualquier constante arbitraria]
Obtenemos
⇒
⇒
⇒
⇒
⇒
Pregunta 6. 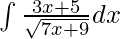
Solución:
Dada integral,
Sea 7x + 9 = t
⇒ x = (t – 9)/7
Al diferenciar ambos lados,
dx = dt/7
Al reemplazar los términos x con t
⇒
⇒
⇒
Usando la fórmula,
[donde c es cualquier constante arbitraria]
⇒
⇒
Al reemplazar t con x términos
⇒
⇒
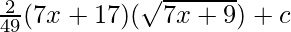
Pregunta 7. 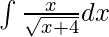
Solución:
Dada integral,
⇒
⇒
Usando la fórmula,
[donde c es cualquier constante arbitraria]
⇒
⇒
⇒
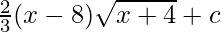
pregunta 8 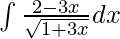
Solución:
Dada integral,
Sea 1 + 3x = t
⇒ x = (t – 1)/3
Al diferenciar ambos lados, obtenemos
dx = dt/3
Al reemplazar x con t
⇒
⇒
⇒
Usando la fórmula,
[donde c es cualquier constante arbitraria]
⇒
Ahora al reemplazar t en términos de x
⇒
⇒
⇒
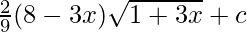
Pregunta 9. 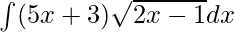
Solución:
Dada integral,
Sea 2x – 1 = t 2
⇒ x = (t 2 + 1)/2
Al diferenciar en ambos lados,
dx = tdt
⇒
⇒
⇒
Usando la fórmula,
[donde c es cualquier constante arbitraria]
⇒
Al reemplazar t con x términos
⇒
⇒
⇒
⇒
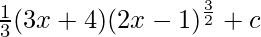
Pregunta 10. 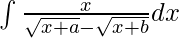
Solución:
Dada integral,
Al multiplicar y dividir la integral dada por
Sabemos que (a + b)(a – b) = a 2 – b 2
⇒
⇒
⇒
⇒
Usando la fórmula,
[donde c es cualquier constante arbitraria]
⇒
⇒
![Rendered by QuickLaTeX.com \frac{2}{a-b}[\frac{(x+a)^\frac{5}{2}+(x+b)^\frac{5}{2}}{5}-(\frac{a(x+a)^\frac{3}{2}+b(x+b)^\frac{3}{2}}{3})]+c](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8e5c69d58d278c1af81116f6df38ec79_l3.png)
Publicación traducida automáticamente
Artículo escrito por prasanthinidamarthy y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
![Procesado por QuickLaTeX.com \frac{1}{2}[\frac{(2x+3)^{\frac{1}{2}+1}}{2(1/2 +1)}-\frac{(2x+3) ^{\frac{-1}{2}+1}}{2(-1/2 +1)}]+c](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-85862f0f019257a7a24b8a078c27edf9_l3.png)
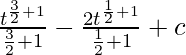
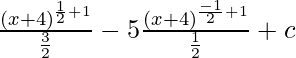
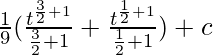
![Rendered by QuickLaTeX.com \frac{1}{3}[\frac{2(3x+2)^{\frac{3}{2}}}{\frac{9}{2}}-\frac{(3x+2)^{\frac{1}{2}}}{\frac{3}{2}}]+c](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-986596361f71e0e461f8cf97508efad1_l3.png)
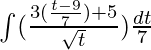
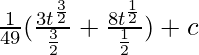
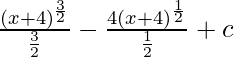
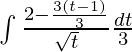
![Rendered by QuickLaTeX.com \frac{1}{3}[\frac{3t^\frac{1}{2}}{\frac{1}{2}}]-\frac{1}{3}[\frac{t^\frac{3}{2}}{\frac{3}{2}}]+c](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4b4e3dfcdd30b7aa9137810470c85f90_l3.png)
![Rendered by QuickLaTeX.com \frac{1}{a-b}[\frac{(x+a)^\frac{5}{2}}{\frac{5}{2}}-{\frac{a(x+a)^{\frac{3}{2}}}{\frac{3}{2}}}+\frac{(x+b)^\frac{5}{2}}{\frac{5}{2}}-{\frac{b(x+b)^{\frac{3}{2}}}{\frac{3}{2}}}]+c](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9eecb61d1d46eea2fb8e3e6c4477408e_l3.png)