Clase 12 Soluciones RD Sharma – Capítulo 19 Integrales indefinidas – Ejercicio 19.8

Pregunta 26. Evalúa ∫ 2cosx – 3senx/ 6cosx + 4senx dx

Solución:

Supongamos que I = ∫ 2cosx – 3senx/ 6cosx + 4senx dx

= ∫ 2cosx – 3senx/ 2(3cosx + 2senx) dx

= ∫ 2cosx – 3senx/ 2(3cosx + 2senx) dx ………..(i)

Sea 3cosx + 2senx = t

d(3cosx + 2senx) = dt

(-3senx + 2cosx) dx = dt

(2cosx – 3senx) dx = dt

Ponga todos estos valores en la ecuación (i), obtenemos

= 1/2 ∫ dt/t

Integrando la ecuación anterior, obtenemos

= 1/2 registro|t| +c

= 1/2 log|3cosx + 2senx| +c

Por lo tanto, I = 1/2 log|3cosx + 2senx| +c

Pregunta 27. Evalúa ∫ cos2x + x + 1/ (x ² + sin2x + 2x) dx

Solución:

Supongamos que I = ∫ cos2x + x + 1/ (x ² + sen2x + 2x) dx (i)

Sea x ² + sen2x + 2x = t

d(x ² + sen2x + 2x) = dt

(2x + 2cos2x + 2) dx = dt

2(x + cos2x + 1) dx = dt

(x + cos2x + 1) dx = dt/2

Ponga todos estos valores en la ecuación (i), obtenemos

= 1/2 ∫ dt/t

Integrando la ecuación anterior, obtenemos

= 1/2 registro|t| +c

= 1/2 log|x ² + sen2x + 2x| +c

Por lo tanto, I = 1/2 log|x ² + sen2x + 2x| +c

Pregunta 28. Evalúa ∫ 1/ cos(x + a) cos(x + b) dx

Solución:

Supongamos que I = ∫ 1/ cos(x + a) cos(x + b) dx

Al multiplicar y dividir la ecuación anterior por sen[(x + b) – (x + a)], obtenemos

= $∫ \frac{1}{cos(x+a) cos(x+b)} × \frac{sin[(x +b)-(x+a)]}{ sin[(x +b)-(x+a)]} dx$

= $∫ \frac{1}{ sin[(x +b)-(x+a)]} × \frac{sin[(x +b)-(x+a)]}{ cos(x+a) cos(x+b)} dx$

= $∫ \frac{1}{sin(b-a)} × \frac{sin[(x +b)cos(x+a)-sin(x+a)cos(x+b)]}{ cos(x+a) cos(x+b)} dx$

= $\frac{1}{sin(b-a)} ∫ \frac{[sin(x +b)cos(x+a)]}{cos(x+a) cos(x+b)} dx- ∫ \frac{[sin(x+a)cos(x+b)]}{ cos(x+a) cos(x+b)} dx$

= 1/ sin(b – a) ∫ tan(x + b) dx – ∫ tan(x + a) dx

Integrando la ecuación anterior, obtenemos

= 1/ sin(b – a) [log(seg(x + b)) – log(seg(x + a))] + c

Por lo tanto, I = 1/ sin(b – a) [log(sec(x + b)/sec(x + a))] + c

Pregunta 29. Evalúa ∫ -senx + 2cosx/(2senx + cosx) dx

Solución:

Supongamos que I = ∫ -senx + 2cosx/(2senx + cosx) dx ………..(i)

Sea 2senx + cosx = t

d(2senx + cosx) = dt

(2cosx – senx) dx = dt

(-senx + 2cosx) dx = dt

Ponga todos estos valores en la ecuación (i), obtenemos

= ∫ dt/t

Integrando la ecuación anterior, obtenemos

= registro|t| +c

= log|2senx + cosx| +c

Por lo tanto, I = log|2senx + cosx| +c

Pregunta 30. Evalúa ∫ cos4x – cos2x/ (sin4x – sin2x) dx

Solución:

Supongamos que I = ∫ cos4x – cos2x/ (sin4x – sin2x) dx

= – ∫ 2sen3x senx / 2cos3x senx dx

= – ∫ sen3x / cos3x dx ………..(i)

Sea cos3x = t

d(cos3x) = dt

-3sen3x dx = dt

– sen3x dx = dt/3

Ponga todos estos valores en la ecuación (i), obtenemos

= 1/3 ∫ dt/t

Integrando la ecuación anterior, obtenemos

= 1/3 registro|t| +c

= 1/3 log|cos3x| +c

Por lo tanto, I = 1/3 log|cos3x| +c

Pregunta 31. Evalúa ∫ secx/ log(secx + tanx) dx

Solución:

Supongamos que I = ∫ secx/ log(secx + tanx) dx ………..(i)

Sea log(secx + tanx) = t

d(log(secx + tanx) = dt

secx dx = dt

Ponga todos estos valores en la ecuación (i), obtenemos

= ∫ dt/t

Integrando la ecuación anterior, obtenemos

= registro |t| +c

= log |log(secx + tanx)| +c

Por lo tanto I = log |log(secx + tanx)| +c

Pregunta 32. Evalúa ∫ cosecx/ log|tanx/2| dx

Solución:

Supongamos que I = ∫ cosecx/ log|tanx/2| dx ………..(i)

Sea log|tanx/2| = t

d(log|tanx/2|) = dt

cosec x dx = dt

Ponga todos estos valores en la ecuación (i), obtenemos

= ∫ dt/t

Integrando la ecuación anterior, obtenemos

= registro |t| +c

= log |log tanx/2| +c

Por lo tanto, I = log |log tanx/2| +c

Pregunta 33. Evalúa ∫ 1/ xlogxlog(logx) dx

Solución:

Supongamos que I = ∫ 1/ xlogxlog(logx) dx ………..(i)

Poner log(logx) = t

d(log(logx)) = dt

1/ xlogx dx = dt

Ponga todos estos valores en la ecuación (i), obtenemos

= ∫ dt/t

Integrando la ecuación anterior, obtenemos

= registro |t| +c

= registro |registro(logx)| +c

Por lo tanto, I = log |log(logx)| +c

Pregunta 34. Evalúa ∫ cosec ² x/ 1 + cot x dx

Solución:

Supongamos que I = ∫ cosec ² x/ 1+cot x dx ………..(i)

Ponga 1 + cotx = t entonces,

d(1 + cox) = dt

– cosec ² x dx = dt

Ponga todos estos valores en la ecuación (i), obtenemos

= – ∫ dt/t

Integrando la ecuación anterior, obtenemos

= – registro |t| +c

= – log |1 + cox| +c

Por lo tanto, I = – log |1 + cotx| +c

Pregunta 35. Evalúa ∫ 10x ⁹ + 10 ^x log _e 10/ (10 ^x + x ¹⁰ ) dx

Solución:

Supongamos que I= ∫ 10x ⁹ + 10 ^x log _e 10/ (10 ^x + x ¹⁰ )dx ………..(i)

Pon 10 ^x + x ¹⁰ = t

d(10 ^x + x ¹⁰ ) = dt

(10 ^x log _e 10 + 10x ⁹ ) dx = dt

Ponga todos estos valores en la ecuación (i), obtenemos

= ∫ dt/t

Integrando la ecuación anterior, obtenemos

= registro |t| +c

= logaritmo |10 ^x + x ¹⁰ | +c

Por lo tanto, I = log |10 ^x + x ¹⁰ | +c

Pregunta 36. Evalúa ∫ 1 – sen2x/ x + cos ² x dx

Solución:

Supongamos que I = ∫ 1 – sin2x/ x + cos ² x dx ………..(i)

Poner x + cos ² x = t

d(x + cos ² x) = dt

(1 – 2senxcosx) dx = dt

(1 – sen2x) dx = dt

Integrando la ecuación anterior, obtenemos

= ∫ dt/t

Integrar el equ anterior entonces, obtenemos

= registro |t| +c

= logaritmo |x + cos ² x| +c

Por lo tanto, I = log |x + cos ² x| +c

Pregunta 37. Evalúa ∫ 1 + tanx/ x + logsecx dx

Solución:

Supongamos que I = ∫ 1 + tanx/ x + logsecx dx ………..(i)

Ponga x + logsecx = t

d(x+logsecx) = dt

(1 + tanx) dx = dt

Ponga todos estos valores en la ecuación (i), obtenemos

= ∫ dt/t

Integrando la ecuación anterior, obtenemos

= registro |t| +c

= log |x + log secx| +c

Por lo tanto, I = log |x + log secx| +c

Pregunta 38. Evalúa ∫ sen2x/ a ² + b ² sen ² x dx

Solución:

Supongamos que I = ∫ sen2x/ a ² + b ² sen ² x dx ………..(i)

Poner a ² + b ² sen ² x = t

d(a ² + b ² sen ² x) = dt

b ² (2senxcosx) dx = dt

sen2x dx = dt/b ²

Ponga todos estos valores en la ecuación (i), obtenemos

= 1/b ² ∫ dt/t

Integrando la ecuación anterior, obtenemos

= 1/b ² registro |t| +c

= 1/b ² log |a ² + b ² sen ² x| +c

Por lo tanto, I = 1/b ² log |a ² + b ² sen ² x| +c

Pregunta 39. Evalúa ∫ x + 1/ x(x + logx) dx

Solución:

Supongamos que I = ∫ x + 1/ x(x + logx) dx ………..(i)

Ponga x + logx = t

d(x + logx) = dt

(1 + 1/x) dx = dt

(x +1)/ x dx = dt

Ponga todos estos valores en la ecuación (i), obtenemos

= ∫ dt/t

Integrando la ecuación anterior, obtenemos

= registro |t| +c

= registro |x + registrox| +c

Por lo tanto, I = log |x + logx| +c

Pregunta 40. Evaluar 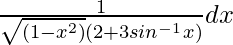$∫ \frac{1}{ \sqrt{(1 - x^2)} (2 + 3sin^{-1}x)} dx$

Solución:

Supongamos que I = $∫ \frac{1}{ \sqrt{(1 - x^2)} (2 + 3sin^{-1}x)} dx$ ………..(i)

Poner 2 + 3sen ^-1 x = t

d(2 + 3sen -1x ⁾ = dt

(3 × 1/ √(1 – x ² )) dx = dt

(1/ √(1 – x ² )) dx = dt/3

Ponga todos estos valores en la ecuación (i), obtenemos

= 1/3 ∫ dt/t

Integrando la ecuación anterior, obtenemos

= 1/3 registro |t| +c

= 1/3 log |2 + 3sen ^-1 x| +c

Por lo tanto, I = 1/3 log |2 + 3sen ^-1 x| +c

Pregunta 41. Evalúa ∫ sec ² x/ tanx + 2 dx

Solución:

Supongamos que I = ∫ sec ² x/ tanx + 2 dx ………..(i)

Ponga tanx + 2 = t

d(tanx + 2) = dt

(seg ² x) dx = dt

Ponga todos estos valores en la ecuación (i), obtenemos

= ∫ dt/t

Integrando la ecuación anterior, obtenemos

= registro |t| +c

= log |tanx + 2| +c

Por lo tanto, I = log |tanx + 2| +c

Pregunta 42. Evalúa ∫ 2cos2x + sec ² x/ sin2x + tanx – 5 dx

Solución:

Supongamos que I = ∫ 2cos2x + sec ² x/ sen2x + tanx – 5 dx ………..(i)

Pon sen2x + tanx – 5 = t

d(sen2x + tanx – 5) = dt

(2cos2x + seg 2x ⁾ dx = dt

Ponga todos estos valores en la ecuación (i), obtenemos

= ∫ dt/t

Integrando la ecuación anterior, obtenemos

= registro |t| +c

= log |sen2x + tanx – 5| +c

Por lo tanto, I = log |sin2x + tanx – 5| +c

Pregunta 43. Evalúa ∫ sin2x/ sin5xsin3x dx

Solución:

Supongamos que I = ∫ sin2x/ sin5xsin3x dx

= ∫ sen(5x – 3x)/ sen5xsen3x dx

= ∫ (sin5x cos3x – cos5x sin3x)/ sin5xsin3x dx [Usando la fórmula: sin(ab) = sina cosb – cosa sinb]

= ∫ (sen5x cos3x)/ sen5xsen3x dx – ∫ (cos5x sen3x)/ sen5xsen3x dx

= ∫ cos3x/sen3x dx – ∫ cos5x/sen5x dx

= ∫ cuna3x dx – ∫ cuna5x dx

Integrando la ecuación anterior, obtenemos

= 1/3 log|sen3x| – 1/5 log|sen5x| +c

Por lo tanto, I = 1/3 log|sen3x| – 1/5 log|sen5x| +c

Pregunta 44. Evalúa ∫ 1 + cotx/ x + logsinx dx

Solución:

Supongamos que I = ∫ 1 + cotx/ x + logsinx dx ………..(i)

Ponga x + logsinx = t

d(x + logsinx) = dt

(1 + cox) dx = dt

Ponga todos estos valores en la ecuación (i), obtenemos

= ∫ dt/t

Integrando la ecuación anterior, obtenemos

= registro |t| +c

= log |x + log senx| +c

Por lo tanto, I = log |x + log senx| +c

Pregunta 45. Evalúa ∫ 1/ √x (√x + 1) dx

Solución:

Supongamos que I = ∫ 1/ √x (√x + 1) dx ………..(i)

Ponga √x + 1 = t

d(√x + 1) = dt

(1/2√x) dx = dt

(1/√x) dx = 2dt

Ponga todos estos valores en la ecuación (i), obtenemos

= 2∫ dt/t

Integrando la ecuación anterior, obtenemos

= 2 registro |t| +c

= 2 registro |√x + 1| +c

Por lo tanto, I = 2 log |√x + 1| +c

Pregunta 46. Evalúa ∫ tan2x tan3x tan 5x dx

Solución:

Supongamos que I = ∫ tan2x tan3x tan 5x dx ………..(i)

Ahora,

tan(5x) = tan(2x + 3x)

tan(5x) = tan2x + tan3x/ (1 – tan2x tan3x) [Usando la fórmula: tan(a + b) = tan a + tan b/ (1- tana tanb)]

tan(5x)(1 – tan2x tan3x) = tan2x + tan3x

(tan5x-tan2x tan3x tan5x) = tan2x + tan3x

tan2x tan3x tan5x = tan5x – tan2x – tan3x ………..(ii)

Usando la ecuación (i) y la ecuación (ii), obtenemos

= ∫ tan5x – tan2x – tan3x dx

Integrando la ecuación anterior, obtenemos

= 1/5 log|seg5x| – 1/2log|seg2x| -1/3log|seg3x| +c

Por lo tanto, I = 1/5 log|seg5x| – 1/2log|seg2x| – 1/3log|seg3x| +c

Pregunta 47. Evalúa ∫ {1 + tanx tan(x + θ)} dx

Solución:

Supongamos que I = ∫ {1 + tanx tan(x + θ)} dx ………..(i)

Como sabemos que,

tan(a – b) = tan a – tan b/ (1+ tan tanb)

tan(x + θ – x) = tan (x + θ) – tan x/ (1+ tan(x + θ) tanx)

tan θ = tan (x + θ) – tan x/ (1+ tan(x + θ) tanx)

(1+ tan(x + θ) tanx) = tan (x + θ) – tan x/tan θ ………..(ii)

Usando la ecuación (i) y (ii), obtenemos

= ∫ bronceado (x + θ) – bronceado x/ bronceado θ dx

= 1/tan θ ∫ tan (x + θ) – tan x dx

Integrando la ecuación anterior, obtenemos

= 1/tan θ [-log|cos(x + θ)| + registro |cosx|] + c

= 1/tan θ [log |cosx| – log|cos(x + θ)|] + c

Por lo tanto, I = 1/tan θ [log {cosx/ cos(x + θ)}] + c

Pregunta 48. Evalúa ∫ sin2x/ sin(x – π/6)sin(x + π/6) dx

Solución:

Supongamos que I = ∫ sin2x/ sin(x – π/6)sin(x + π/6) dx ………..(i)

= ∫ sen2x/ sen ² x – sen ² π/6 dx

= ∫ sen2x/ sen ² x – 1/4 dx

Pon sen ² x – 1/4 = t

d(sen ² x – 1/4) = dt

(2senx cosx) dx = dt

(sen2x) dx = dt

Ponga todos estos valores en la ecuación (i), obtenemos

= ∫ dt/t

Integrando la ecuación anterior, obtenemos

= registro |t| +c

= registro |√x + 1| +c

Por lo tanto, I = log |sen ² x – 1/4| +c

Pregunta 49. Evalúa ∫ e ^x-1 + x ^e-1 / e ^x + x ^e dx

Solución:

Supongamos que I = ∫ e ^x-1 + x ^e-1 / e ^x + x ^e dx ………..(i)

= 1/e ∫ e ^x + ex ^e-1 / e ^x + x ^e dx

= 1/e ∫ e ^x + ex ^e-1 / e ^x + x ^e dx

Pon e ^x + x ^e = t

d(e ^x + x ^e ) = dt

( ex + ex ^{e-1 ) dx}⁼ dt

( ex + ex ^{e-1 ) dx}⁼ dt

Ponga todos estos valores en la ecuación (i), obtenemos

= 1/e ∫ dt/t

Integrando la ecuación anterior, obtenemos

= 1/e registro |t| +c

= 1/e log |e ^x + x ^e | +c

Por lo tanto, I = 1/e log |e ^x + x ^e | +c

Pregunta 50. Evalúa ∫ 1/senx cos ² x dx

Solución:

Supongamos que I = ∫ 1/senx cos ² x dx

= ∫sen ² x + cos ² x/senx cos ² x dx

= ∫sen ² x/senx cos ² x + cos ² x/senx cos ² x dx

= ∫senx/ cos ² x + cosecx dx

= ∫secx tanx dx +∫ cosecx dx

Integrando la ecuación anterior, obtenemos

= seg x + log|tanx/2| +c

Por lo tanto, I = sec x + log|tanx/2| +c

Pregunta 51. Evalúa ∫ 1/cos3x – cosx dx

Solución:

Supongamos que I = ∫ 1/cos3x – cosx dx

∫ 1/cos3x – cosx dx = ∫ sen ² x + cos ² x / 4cos ³ x – 4cosx dx

= ∫ sen ² x + cos ² x / 4 cos (cos ² x – 1) dx

= -1/4 ∫ sen ² x/ sen ² xcosx dx + ∫ cos ² x / sen ² xcosx dx

= -1/4 ∫ secx + cosecx cotx dx

Integrando la ecuación anterior, obtenemos

= -1/4 [log|secx + tanx| – cosecx] + c

Por lo tanto, I = 1/4 [cosecx + log|secx + tanx|] + c

Publicación traducida automáticamente

Artículo escrito por yogirao y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 12 Soluciones RD Sharma – Capítulo 19 Integrales indefinidas – Ejercicio 19.8 | conjunto 2

Pregunta 26. Evalúa ∫ 2cosx – 3senx/ 6cosx + 4senx dx

Pregunta 27. Evalúa ∫ cos2x + x + 1/ (x ² + sin2x + 2x) dx

Pregunta 28. Evalúa ∫ 1/ cos(x + a) cos(x + b) dx

Pregunta 29. Evalúa ∫ -senx + 2cosx/(2senx + cosx) dx

Pregunta 30. Evalúa ∫ cos4x – cos2x/ (sin4x – sin2x) dx

Pregunta 31. Evalúa ∫ secx/ log(secx + tanx) dx

Pregunta 32. Evalúa ∫ cosecx/ log|tanx/2| dx

Pregunta 33. Evalúa ∫ 1/ xlogxlog(logx) dx

Pregunta 34. Evalúa ∫ cosec ² x/ 1 + cot x dx

Pregunta 35. Evalúa ∫ 10x ⁹ + 10 ^x log _e 10/ (10 ^x + x ¹⁰ ) dx

Pregunta 36. Evalúa ∫ 1 – sen2x/ x + cos ² x dx

Pregunta 37. Evalúa ∫ 1 + tanx/ x + logsecx dx

Pregunta 38. Evalúa ∫ sen2x/ a ² + b ² sen ² x dx

Pregunta 39. Evalúa ∫ x + 1/ x(x + logx) dx

Pregunta 40. Evaluar $∫ \frac{1}{ \sqrt{(1 - x^2)} (2 + 3sin^{-1}x)} dx$

Pregunta 41. Evalúa ∫ sec ² x/ tanx + 2 dx

Pregunta 42. Evalúa ∫ 2cos2x + sec ² x/ sin2x + tanx – 5 dx

Pregunta 43. Evalúa ∫ sin2x/ sin5xsin3x dx

Pregunta 44. Evalúa ∫ 1 + cotx/ x + logsinx dx

Pregunta 45. Evalúa ∫ 1/ √x (√x + 1) dx

Pregunta 46. Evalúa ∫ tan2x tan3x tan 5x dx

Pregunta 47. Evalúa ∫ {1 + tanx tan(x + θ)} dx

Pregunta 48. Evalúa ∫ sin2x/ sin(x – π/6)sin(x + π/6) dx

Pregunta 49. Evalúa ∫ e ^x-1 + x ^e-1 / e ^x + x ^e dx

Pregunta 50. Evalúa ∫ 1/senx cos ² x dx

Pregunta 51. Evalúa ∫ 1/cos3x – cosx dx

Deja una respuesta Cancelar la respuesta

Pregunta 26. Evalúa ∫ 2cosx – 3senx/ 6cosx + 4senx dx

Pregunta 27. Evalúa ∫ cos2x + x + 1/ (x 2 + sin2x + 2x) dx

Pregunta 28. Evalúa ∫ 1/ cos(x + a) cos(x + b) dx

Pregunta 29. Evalúa ∫ -senx + 2cosx/(2senx + cosx) dx

Pregunta 30. Evalúa ∫ cos4x – cos2x/ (sin4x – sin2x) dx

Pregunta 31. Evalúa ∫ secx/ log(secx + tanx) dx

Pregunta 32. Evalúa ∫ cosecx/ log|tanx/2| dx

Pregunta 33. Evalúa ∫ 1/ xlogxlog(logx) dx

Pregunta 34. Evalúa ∫ cosec 2 x/ 1 + cot x dx

Pregunta 35. Evalúa ∫ 10x 9 + 10 x log e 10/ (10 x + x 10 ) dx

Pregunta 36. Evalúa ∫ 1 – sen2x/ x + cos 2 x dx

Pregunta 37. Evalúa ∫ 1 + tanx/ x + logsecx dx

Pregunta 38. Evalúa ∫ sen2x/ a 2 + b 2 sen 2 x dx

Pregunta 39. Evalúa ∫ x + 1/ x(x + logx) dx

Pregunta 40. Evaluar

Pregunta 41. Evalúa ∫ sec 2 x/ tanx + 2 dx

Pregunta 42. Evalúa ∫ 2cos2x + sec 2 x/ sin2x + tanx – 5 dx

Pregunta 43. Evalúa ∫ sin2x/ sin5xsin3x dx

Pregunta 44. Evalúa ∫ 1 + cotx/ x + logsinx dx

Pregunta 45. Evalúa ∫ 1/ √x (√x + 1) dx

Pregunta 46. Evalúa ∫ tan2x tan3x tan 5x dx

Pregunta 47. Evalúa ∫ {1 + tanx tan(x + θ)} dx

Pregunta 48. Evalúa ∫ sin2x/ sin(x – π/6)sin(x + π/6) dx

Pregunta 49. Evalúa ∫ e x-1 + x e-1 / e x + x e dx

Pregunta 50. Evalúa ∫ 1/senx cos 2 x dx

Pregunta 51. Evalúa ∫ 1/cos3x – cosx dx

Deja una respuesta Cancelar la respuesta

Pregunta 27. Evalúa ∫ cos2x + x + 1/ (x ² + sin2x + 2x) dx

Pregunta 34. Evalúa ∫ cosec ² x/ 1 + cot x dx

Pregunta 35. Evalúa ∫ 10x ⁹ + 10 ^x log _e 10/ (10 ^x + x ¹⁰ ) dx

Pregunta 36. Evalúa ∫ 1 – sen2x/ x + cos ² x dx

Pregunta 38. Evalúa ∫ sen2x/ a ² + b ² sen ² x dx

Pregunta 40. Evaluar $∫ \frac{1}{ \sqrt{(1 - x^2)} (2 + 3sin^{-1}x)} dx$

Pregunta 41. Evalúa ∫ sec ² x/ tanx + 2 dx

Pregunta 42. Evalúa ∫ 2cos2x + sec ² x/ sin2x + tanx – 5 dx

Pregunta 49. Evalúa ∫ e ^x-1 + x ^e-1 / e ^x + x ^e dx

Pregunta 50. Evalúa ∫ 1/senx cos ² x dx