Pregunta 49. 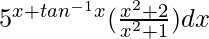
Solución:
Dado que I =
……..(i)
x + tan -1 x = t entonces,
d(x + bronceado -1 x) = dt
(1 + 1/(1 + x 2 ))dx = dt
((1 + x 2 + 1)/(1 + x 2 ))dx = dt
((x 2 + 2))/((x 2 + 1)) dx = dt
Ahora, al poner x + tan -1 x = t y ((x 2 + 2)/(x 2 + 1))dx = dt en la ecuación (i), obtenemos
yo = ∫5 t dt
= 5 t /(log5) + c
=
/(log5) + c
Por lo tanto, yo =
/(log5) + c
Pregunta 50. 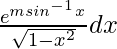
Solución:
Dado que I =
……(i)
msin -1 x = t entonces,
d(msen -1 x) = dt
m 1/√(1 – x 2 ) dx = dt
dx/√(1 – x 2 ) = dt/m
Ahora, al poner msin -1 x = t y dx/√(1 – x 2 ) = dt/m en la ecuación (i), obtenemos
yo = ∫e t dt/m
= 1/yo t +c
=
Por lo tanto, yo =
Pregunta 51. ∫(cos√x)/√x dx
Solución:
Dado que I = ∫(cos√x)/√x dx
√x = t entonces,
1/(2√x) dx = dt
Ahora,
= ∫ (cos√x)/√x dx
= 2∫ costdt2
= 2sent + c
Por lo tanto, yo = 2sin√x + c
Pregunta 52. ∫sen(tan -1 x)/(1 + x 2 ) dx
Solución:
Dado que I = ∫sin(tan -1 x)/(1 + x 2 ) dx ……(i)
tan -1 = t entonces,
d(tan -1 x) = dt
1/(1 + x 2 ) dx = dt
Ahora, al poner tan -1 x = t y dx/(1 + x 2 ) = dt en la ecuación (i), obtenemos
yo = ∫ sentdt
= -cost + c
= -cos(tan -1 x) + c
Por lo tanto, yo = -cos(tan -1 x) + c
Pregunta 53. ∫(sen(logx))/x dx
Solución:
Dado que I = ∫(sin(logx))/x dx ……..(i)
logx = t entonces,
d(logx) = dt
1/x dx = dt
Ahora, al poner logx = t y 1/x dx = dt en la ecuación (i), obtenemos
yo = ∫sentdt
= -cost + c
= -cos(logx) + c
Por lo tanto, yo = -cos(logx) + c
Pregunta 54.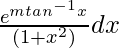
Solución:
Dado que yo =
Consideremos tan -1 x = t, entonces
Al derivar la función anterior tenemos,
1/(1 + x 2 ) dx = dt
= ∫e mt × dt
=
= e mt /m
Al sustituir el valor de t, tenemos
yo =
+ c
Pregunta 55. ∫x/(√(x 2 + a 2 ) + √(x 2 – a 2 )) dx
Solución:
Dado que I = ∫x/(√(x 2 + a 2 ) + √(x 2 – a 2 )) dx
= ∫ x/(√(x 2 + a²) + √(x 2 – a 2 )) × (√(x 2 + a 2 ) – √(x 2 – a 2 ))/(√(x 2 + a 2 ) – √(x 2 – a 2 )) dx
= ∫ x(√(x 2 + un 2 ) – √(x 2 – un 2 ))/(x 2 + un 2 – x 2 + un 2 ) dx
= ∫ x/(2a 2 ) (√(x 2 + a 2 ) – √(x 2 – a 2 ))dx
yo = 1/(2a 2 ) ∫x(√(x 2 + a 2 ) – √(x 2 – a 2 ))dx ……(i)
Consideremos x 2 = t entonces,
Al derivar la función anterior tenemos,
d(x2 ) = dt
2xdx = dt
xdx = dt/2
Ahora, al poner x 2 = t y xdx = dt/2 en la ecuación (i), obtenemos
yo = 1/(2a 2 ) ∫(√(t + a 2 ) – √(t – a 2 )) dx/2
Por lo tanto, I = 1/(4a 2 ) [2/3 (t + a 2 ) 3/2 – 2/3 (t – a 2 ) 3/2 ] + c
Pregunta 56. ∫x(tan -1 x 2 )/(1 + x 4 ) dx
Solución:
Dado que I = ∫x(tan -1 x 2 )/(1 + x 4 ) dx ……..(i)
Consideremos tan -1 x 2 = t entonces,
Al derivar la función anterior tenemos,
d(tan -1 x 2 ) = dt
(1 × 2x)/(1 + (x 2 ) 2 ) dx = dt
(1 × x)/(1 + x 4 ) dx = dt/2
Ahora, al poner tan -1 x 2 = t y x/(1 + x 4 ) dx = dt/2 en la ecuación (i), obtenemos
yo = ∫ t dx/2
= 1/2 ∫tdt
= 1/2 × t 2 /2 + c
= t 2 /4 + c – 1
= (tan -1 x 2 ) 2 /4 + c
Por lo tanto, yo = 1/4 (tan -1 x 2 ) 2 + c
Pregunta 57. ∫(sen -1 x) 3 /√(1 – x 2 ) dx
Solución:
Dado que I = ∫(sen -1 x) 3 /√(1 – x 2 ) dx ……(i)
Consideremos sen -1 x = t entonces,
Al derivar la función anterior tenemos,
d(sen -1 x) = dt
1/√(1 – x 2 ) dx = dt
Ahora, al poner sen -1 x = t y 1/√(1 – x 2 ) dx = dt en la ecuación (i), obtenemos
yo = ∫t 3 dt
= t 4 /4 + c
Por tanto, I = 1/4 (sen -1 x) 4 + c
Pregunta 58.∫(sen(2 + 3logx))/x dx
Solución:
Dado que I = ∫(sin(2 + 3logx))/x dx ……..(i)
Consideremos 2 + 3logx = t entonces,
Al derivar la función anterior tenemos,
d(2 + 3logx) = dt
3 1/x dx = dt
dx/x = dt/3
Ahora al poner 2 + 3logx = t y dx/x = dt/3 en la ecuación (i), obtenemos
yo = ∫sent dt/3
= 1/3(-cost) + ct
= -1/3 cos(2 + 3logx) + c
Por lo tanto, yo = -1/3 cos(2 + 3logx) + c
Pregunta 59. 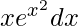
Solución:
Dado que I =
……(i)
Consideremos x 2 = t entonces,
Al derivar la función anterior tenemos,
d(x2 ) = dt
2xdx = dt
xdx = dt/2
Ahora, al poner x 2 = t y xdx = dt/2 en la ecuación (i), obtenemos
yo = ∫e t dt/2
= 1/2 e t +c
= 1/2
+ do
Por lo tanto, yo = 1/2
+ c
Pregunta 60. ∫e 2x /(1 + e x ) dx
Solución:
Dado que I = ∫e 2x /(1 + e x ) dx …….(i)
Consideremos 1 + e x = t entonces,
Al derivar la función anterior tenemos,
d(1 + e x ) = dt
e x dx = dt
dx = dt/ ex
Ahora, al poner 1 + e x = t y dx = dt/e x en la ecuación (i), obtenemos
yo = ∫e 2x /t × dt/e x
= ∫e x /t dt
= ∫ (t – 1)/t dt
= ∫ (t/t – 1/t)dt
= t – log|t| +c
= (1 + e x ) – log|1 + e x | +c
Por lo tanto, yo = 1 + e x – log|1 + e x | +c
Pregunta 61. ∫(seg 2 √x)/√x dx
Solución:
Dado que I = ∫(seg 2 √x)/√x dx ……(i)
Consideremos √x = t entonces,
Al derivar la función anterior tenemos,
d(√x) = dt
1/(2√x) dx = dt
dx = 2√x dt
dx = 2tdt [√x = t])
Ahora, al poner √x = t y dx = 2tdt en la ecuación (i), obtenemos
yo = ∫ (seg 2 t)/t × 2tdt
= 2∫ seg 2 tdt
= 2tant + c
= 2tan√x + c
Por lo tanto, yo = 2tan√x + c
Pregunta 62. ∫tan 3 2x seg2x dx
Solución:
Dado que I = ∫tan 3 2x sec2x dx
= tan 2 2x tan2x seg2x
= (seg 2 2x – 1)tan2x seg2x
= seg 2 2x.tan2xsec2x – tan2xsec2x
= ∫ seg 2 2xtan2xsec2xdx – ∫tan2xsec2xdx
= ∫ seg 2 2xtan2xsec2xdx – (sec2x)/2 + c
Consideremos sec2x = t
2sec2xtan2xdx = dt
yo = 1/2 ∫t 2 dt – (seg2x)/2 + c
yo = t 3 /6 – (seg2x)/2 + c
Por lo tanto, I = (seg2x) 3 /6 – (seg2x)/2 + c
Pregunta 63. ∫(x + √(x + 1))/(x + 2) dx
Solución:
Dado que I = ∫(x+√(x+1))/(x+2) dx …….(i)
Consideremos x + 1 = t 2 entonces,
Al derivar la función anterior tenemos,
d(x + 1) = d(t 2 )
dx = 2tdt
Ahora, al poner x + 1 = t 2 y dx = 2tdt en la ecuación (i), obtenemos
yo = ∫ (x + √(t 2 ))/(x + 2) 2tdt
= 2∫((t 2 – 1) + t)/((t 2 – 1) + 2) × tdt [x + 1 = t 2 ]
= 2∫(t 2 + t – 1)/(t 2 + 1) tdt
= 2∫ (t 3 + t 2 – t)/(t 2 + 1) dt
= 2[∫ t 3 /(t 2 + 1) dt + ∫ t 2 /(t 2 + 1) dt – ∫ t/(t 2 + 1) dt]
I = 2[∫t 3 /(t 2 + 1) dt + ∫t 2 /(t 2 + 1) dt – ∫t/(t 2 + 1) dt] ……(ii)
Sea I 1 = ∫t 3 /(t 2 + 1) dt
yo 2 = ∫t 2 /(t 2 + 1) dt
y yo 3 = ∫t/(t 2 + 1) dt
Ahora, yo 1 = ∫t 3 /(t 2 + 1) dt
= ∫(t – t/(t 2 + 1))dt
= t 2 /2 – 1/2 log(t 2 + 1)
I 1 = t 2 /2 – 1/2 log(t 2 + 1) + c 1 ……..(iii)
Ya que, yo 2 = ∫t 2 /(t 2 + 1) dt
= ∫ (t 2 + 1 – 1)/(t 2 + 1) dt
= ∫(t 2 + 1)/(t 2 + 1) dt – ∫1/(t 2 + 1) dt
= ∫dt – ∫1/(t 2 + 1) dt
yo 2 = t – tan -1 (t 2 ) + c 2 ………….(iv)
y,
yo 3 = ∫t/(t 2 + 1) dt
= 1/2 log(1 + t 2 ) + c 3 ……..(v)
Usando las ecuaciones (ii), (iii), (iv) y (v), obtenemos
yo = 2[t 2 /2 – 1/2 log(t 2 + 1) + c 1 + t-tan -1 (t 2 ) + c 2 – 1/2 log(1 + t 2 ) + do3 ] _
= 2[t 2 /2 + t-tan -1 (t 2 ) – log(1 + t 2 ) + c 1 + c 2 + c 3 ]
= 2[t 2 /2 + t – tan -1 (t 2 ) – log(1 + t 2 ) + c 4 [Poner c 1 + c 2 + c 3 = c 4 ]
= t 2 + 2t – 2tan -1 (t 2 ) – 2log(1 + t 2 ) + 2c 4
= (x + 1) + 2√(x + 1) – 2tan -1 (√(x + 1)) – 2log(1 + x + 1) + 2c 4
= (x + 1) + 2√(x + 1) – 2tan -1 (√(x + 1)) – 2log(x + 2) + c [Poner 2c 4 = c]
Por lo tanto, yo = (x + 1) + 2√(x + 1) – 2tan -1 (√(x + 1)) – 2log(x + 2) + c
Pregunta 64. 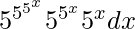
Solución:
Dado que I =
…….(1)
Consideremos
= t entonces
Al derivar la función anterior tenemos,
d(
) = dt
×
× 5 x × (log5) 3 dx = dt
dx = dt/((log5)^3 ))
Ahora, al poner
= t y
dx = dt/((log5)^3 )) en la ecuación (i), obtenemos
yo = ∫dt/((log5) 3 )
= 1/((log5) 3 ) ∫dt
= t/((log5)^3) + c
Por lo tanto, yo =
/((log5) 3 ) + c)
Pregunta 65. ∫1/(x√(x 4 – 1)) dx
Solución:
Dado que I = ∫1/(x√(x 4 – 1)) dx ……….(i)
Consideremos x 2 = t entonces,
Al derivar la función anterior tenemos,
d(x2 ) = dt
2xdx = dt
dx = dt/2x
Ahora, al poner x 2 = t y dx = dt/2x en la ecuación (i), obtenemos
yo = ∫ 1/(x√(t 2 – 1)) × dt/2x
= 1/2 ∫ 1/(x 2 √(t 2 – 1)) dt
= 1/2 ∫ 1/(t√(t 2 – 1)) dt
= 1/2 seg -1 t + c
= 1/2 seg -1 x 2 + c
Por lo tanto, I = 1/2 seg -1 x 2 + c
Pregunta 66. ∫√(e x – 1) dx
Solución:
Dado que I = ∫√(ex – 1) dx ……..(i)
Consideremos e x – 1 = t 2 entonces,
Al derivar la función anterior tenemos,
d(ex – 1) = dt(t 2 )
e x dx = 2tdt
dx = 2t/e x dt
dx = 2t/(t 2 + 1) dt [e x – 1 = t 2 ]
Ahora, al poner e x – 1 = t² y dx = 2tdt/(t 2 + 1) en la ecuación (i), obtenemos
yo = ∫√(t 2 ) × 2tdt/(t 2 + 1)
= 2∫(t × t)/(t 2 + 1) dt
= 2∫t 2 /(t 2 + 1) dt
= 2∫(t 2 + 1 – 1)/(t 2 + 1) dt
= 2∫[(t 2 + 1)/(t 2 + 1) – 1/(t 2 + 1)]dt
= 2∫dt – 2∫1/(t 2 + 1) dt
= 2t – 2tan -1 (t) + c
= 2√(e x – 1) – 2tan -1 (√(e x – 1)) + c
Por lo tanto, yo = 2√(ex – 1) – 2tan -1 √(ex – 1) + c
Pregunta 67. ∫ 1/(x + 1)(x 2 + 2x + 2) dx
Solución:
Dado que I = ∫1/(x + 1)(x 2 + 2x + 2) dx
= ∫1/(x + 1)((x + 1) 2 + 1) dx
Consideremos x + 1 = tan u entonces, [tanu = Perpendicular/Base = (x + 1)/1]
Al derivar la función anterior tenemos,
dx = sec 2 u du [Hipotenusas = √(x 2 + 2x + 2)]
I = ∫sec 2 u/tanu(tan 2 u + 1) du
= ∫ cosu/sinu du
= registro| seno |+c
= registro| sen(x + 1)| + c [Como sabemos, sin(x + 1) = P/H = (x + 1)/√(x 2 + 2x + 2)]
Por lo tanto, I = log| x + 1/√(x2 + 2x + 2)| +c
Pregunta 68. ∫x 5 /√(1 + x 3 ) dx
Solución:
Dado que I = ∫ x 5 /(√(1 + x 3 )) dx …….(i)
Consideremos 1 + x 3 = t 2 , entonces
Al derivar la función anterior tenemos,
d(1 + x 3 ) = d(t 2 )
3x 2 dx = 2t * dt
dx = 2t dt/3x 2
Ahora, al poner 1 + x 3 = t 2 y dx = 2tdt/3x 2 en la ecuación (i), obtenemos
yo = ∫ x 5 /√t 2 * 2t/3x 2 dt
= ∫x 5 /t * 2t/3x 2 dt
= 2/3∫x 3 dt
= 2/3 ∫( t 2 – 1) dt
= 2/3[t 3 /3 – 2t/3] + c
Por lo tanto, yo = 2/9(1 + x 3 ) 3/2 – 2 √(1 + x 2 )/3 + c
Pregunta 69. ∫4x 3 √(5 – x 2 ) dx
Solución:
Dado que I = ∫4x 3 √(5 – x 2 ) dx ……(i)
Consideremos 5 – x 2 = t 2 entonces,
Al derivar la función anterior tenemos,
d(5 – x 2 ) = t 2
-2xdx = 2tdt
dx = (-t)/x dt
Ahora, al poner 5 – x 2 = t 2 y dx = (-t)/x dt en la ecuación (i), obtenemos
yo = ∫4x 3 √(t 2 ) × (-t)/x dt
= -4∫ x 2 t × tdt
= -4∫(5 – t 2 ) t 2 dt [5 – x 2 = t 2 ]
= -4∫(5t 2 – t 5 )dt
= -20×t 3 /3 + 4 t 5 /5 + c
= (-20)/3 × t 3 + 4/5 × t 5 + c
= (-20)/3 × (5 – x 2 ) 3/2 + 4/5 × (5 – x 2 ) 5/2 + c
yo = (-20)/3 × (5 -x 2 ) 3/2 + 4/5 × (5 – x 2 ) 5/2 + c
Pregunta 70. ∫1/(√x + x) dx
Solución:
Dado que I = ∫1/(√x + x) dx ……..(i)
Consideremos √x = t entonces,
Al derivar la función anterior tenemos,
d(√x) = dt
1/(2√x) dx = dt
dx = 2√x dt
Ahora al poner √x = t y 2√x dt = dx en la ecuación (i), obtenemos
I = ∫1/(t + t 2 ) 2t × dt [Ya que √x = t y x = t 2 ]
= ∫2t/(t(1 + t)) dt
= 2∫t/(1 + t) dt
= 2log|1 + t| +c
= 2log|1 + √x| +c
Por lo tanto, yo = 2log|1 + √x|+c
Pregunta 71. ∫1/(x 2 (x 4 + 1) 3/4 ) dx
Solución:
Dado que I = 1/(x 2 (x 4 +1) 3/4 )
Multiplicando y dividiendo por x -3 , obtenemos
(x -3 /(x 2 x -3 (x 4 + 1) 3/4 ) = (x -3 (x 4 + 1) -3/4 /(x 2 x -3 ))
= (x 4 + 1) -3/4 /(x 5 (x 4 ) -3/4
= 1/x 5 ((x 4 + 1)/x 4 ) -3/4
= 1/x 5 (1 + 1/x 4 ) -3/4
Consideremos 1/x 4 = t
-4/x 5 dx = dt
1/x 5 dx = -dt/4
yo = ∫ 1/x 5 (1 + 1/x 4 ) -3/4 dx
= -1/4 ∫(1 + t) -3/4 dt
= -1/4 [(1 + t) 1/4 )/(1/4)] + c
= -1/4(1 + 1/x 4 ) 1/4 /(1/4) + c
Por tanto, yo = -(1 + 1/x 4 ) 1/4 + c
Pregunta 72. ∫(sen 5 x)/(cos 4 x) dx
Solución :
Dado que I = ∫(sen 5 x)/(cos 4 x) dx ……(i)
Consideremos cosx = t entonces,
Al derivar la función anterior tenemos,
d(cosx) = dt
-sinxdx = dt
dx = -dt/(senx)
Ahora, al poner cosx = t y dx = -dt/(sinx) en la ecuación (i), obtenemos
yo = ∫(sen 5 x)/t 4 × -dt/(senx)
= -∫(sen 4 x)/t 4 dt
= -∫(1 – cos 2 x) 2 /t 4 dt
= -∫(1 – t 2 ) 2 /t 4 dt
= -∫(1 + t 4 – 2t 2 )/t 4 dt
= -∫(1/t 4 + t 4 /t 4 – (2t 2 )/t 4 )dt
= -∫(t -4 + 1 – 2t -2 )dt
= -[t -3 /(-3) + t – 2 t -1 /(-1)] + c
= 1/3 * 1/t 3 – t – 1/t + c
Por tanto, I = 1/3 * 1/cos 3 x – cosx -2/cosx + c
Publicación traducida automáticamente
Artículo escrito por anandchaturvedirishra y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA