Evalúa las siguientes integrales:
Pregunta 1. ∫(logx)/x dx
Solución:
Dado que, I = ∫(logx)/x dx
Consideremos logx = t
Ahora diferenciando ambos lados obtenemos,
d(logx) = dt
1/x dx = dt
dx = xdt
Entonces, ponemos logx = t y dx = xdt, obtenemos
yo = ∫ t/x × (x)dt
= ∫ tdt
= t 2 /2 + c
= (logx) 2 /2 + c
Por lo tanto, yo = (logx) 2 /2 + c
Pregunta 2.∫(log(1 + 1/x))/(x(1 + x)) dx
Solución:
Dado que I = ∫(log(1 + 1/x))/(x(1 + x)) dx ……(i)
Consideremos log(1 + 1/x) = t entonces
Al diferenciar ambos lados obtenemos,
d[log(1 + 1/x)]=dt
1/(1 + 1/x) × (-1)/x 2 dx = dt
1/((x + 1)/x) × (-1)/x 2 dx = dt
(-x)/(x 2 (x + 1)) dx = -dt
dx/(x(x + 1)) = -dt
Ahora, al poner log(1 + 1/x) = t y dx/(x(x + 1)) = -dt en la ecuación (i), obtenemos
yo = ∫t × -dt
= -t 2 /2 + c
= -1/2 [log(1 + 1/x)] 2 + c
Por lo tanto, yo = -1/2 [log(1 + 1/x)] 2 + c
Pregunta 3. ∫((1 + √x ) 2 )/√x dx
Solución:
Dado que I = ∫((1 + √x) 2 )/√x dx
Consideremos (1 + √x) = t entonces,
Al diferenciar ambos lados obtenemos,
d(1 + √x) = dt
1/(2√x) dx = dt
dx = dt × 2√x
Ahora al poner (1 + √x) = t y dx = dt × 2√x, obtenemos
yo = ∫t 2 /√x × dt × 2√x
= 2∫t 2 dt
= 2 × t 3 /3 + c
= 2/3[1 + √x] 3 + c
Por lo tanto, yo = 2/3(1 + √x) 3 + c
Pregunta 4. ∫√(1 + e x ) e x d
Solución:
Dado que I = ∫√(1 + e x ) e x dx ……(i)
Consideremos 1 + e x = t entonces,
Al diferenciar ambos lados obtenemos,
d(1 + e x ) = dt
e x dx = dt
dx = dt/ ex
Ahora, al poner 1 + e x = t y dx = dt/e x en la ecuación (i), obtenemos
yo = ∫√t × e x × dt/e x
= ∫ t 1/2 dt
= 2/3t 3/2 + c
= 2/3 (1 + e x ) 3/2 +c
Pregunta 5. ∫∛(cos 2 x) senx dx
Solución:
Dado que I = ∫∛(cos 2 x) senx dx ……(i)
Consideremos cosx = t entonces,
Al diferenciar ambos lados obtenemos,
d(cosx) = dt
-sinxdx = dt
dx = -dt/(senx))
Ahora, al poner cosx = t y dx = -dt/(sinx) en la ecuación (i), obtenemos
yo = ∫∛(t 2 ) sinx × (-dt)/(sinx)
= -∫t 2/3 senx dt/(senx)
= -∫ t 2/3 dt
= -3/5 × t 5/3
Por lo tanto, yo = -3/5(cosx) 5/3 + c
Pregunta 6. ∫e x /(1 + e x ) 2 dx
Solución:
Dado que I = ∫e x /(1 + e x ) 2 dx …….(i)
Consideremos 1 + e x = t entonces,
Al diferenciar ambos lados obtenemos,
d(1 + e x ) = dt
e x dx = dt
dx = dt/ ex
Ahora, al poner 1 + e x = t y dx = dt/e x en la ecuación (i), obtenemos
yo = ∫e x /t 2 × dt/e x
= ∫dt/t 2
= ∫t -2 dt
= -t -1 + c
= -1/t + c
= -1/(1 + e x ) + c
Por lo tanto, yo = -1/(1 + e x ) + c
Pregunta 7. ∫cot 3 x cosec 2 x dx
Solución:
Dado que I = ∫cot 3 x cosec 2 x dx …….(i)
Consideremos cotx = t entonces,
Al diferenciar ambos lados obtenemos,
d(cotx) = dt
-coseg 2 x dx = dt
dx = -dt/coseg 2 x
Ahora, al poner cotx = t y dx = -dt/(cosec 2 x) en la ecuación (i), obtenemos
yo = ∫ t 3 cosec 2 x × (-dt)/(cosec 2 x)
= -∫ t 3 dt
= -t 4 /4 + c
= -(cuna 4 x)/4 + c
Por lo tanto, yo = -(cot 4 x)/4 + c
pregunta 8 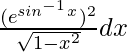
Solución:
Dado que I =
[Tex] [/Tex] …….(i)
Consideremos sen -1 x = t entonces,
Al diferenciar ambos lados obtenemos,
d(sen -1 x) = dt
1/√(1 – x 2 )dx = dt
dx = √(1 – x 2 ) dt)
Ahora, al poner sen -1 x = t y dx = √(1 – x 2 ) dt en la ecuación (i), obtenemos
yo = ∫ (e t ) 2 /√(1 – x 2 ) × √(1 – x 2 ) dt
= ∫e 2t dt
= e 2t /2 + c
=
+ c
Por lo tanto, yo =
+ c
Pregunta 9. ∫(1 + sinx)/√(x – cosx) dx
Solución:
Dado que I = ∫(1 + sinx)/√(x – cosx) dx ……..(i)
Consideremos x – cosx = t, entonces
Al diferenciar ambos lados obtenemos,
d(x – cosx) = dt
[1 – (-senx)]dx = dt
(1 + senx)dx = dt
Ahora, al poner x – cosx = t y (1 + sinx)dx = dt en la ecuación (i), obtenemos
yo = ∫ dt/√t
= ∫ t -1/2 dt
= 2t 1/2 + c
= 2(x – cosx) 1/2 + c
Por lo tanto, yo = 2√(x – cosx) + c
Pregunta 10. ∫1/(√(1 – x 2 ) (sen -1 x) 2 ) dx
Solución:
Dado que I = ∫1/(√(1 – x 2 ) (sin -1 x) 2 ) dx …..(i)
Consideremos sen -1 x = t entonces,
Al diferenciar ambos lados obtenemos,
d(sen -1 x) = dt
1/√(1 – x 2 ) dx = dt
Ahora, al poner sen -1 x = t y 1/√(1 – x 2 ) dx = dt en la ecuación (i), obtenemos
yo = ∫dt/t 2
= ∫t -2 dt
= -t -1 + c
= (-1)/t + c
= (-1)/(sen -1 x) + c
Por lo tanto, yo = (-1)/(sen -1 x) + c
Pregunta 11. ∫(cotx)/√(senx) dx
Solución:
Dado que I = ∫(cotx)/√(sinx) dx …….(i)
Consideremos senx = t entonces,
Al diferenciar ambos lados obtenemos,
d(senx) = dt
cosxdx = dt
Ahora, yo = ∫(cotx)/√(sinx) dx
= ∫(cosx)/(senx√(senx)) dx
= ∫ cosx/(senx) 3/2 dx
= ∫ cosx/(senx) 3/2 dx …….(ii)
Ahora, al poner senx = t y cosxdx = dt en la ecuación (ii), obtenemos
yo = ∫ dt/t 3/2
= ∫ t -3/2 dt
= -2t -1/2 + c
= -2/√t + c
= -2/√(senx) + c
yo = -2/√senx + c
Pregunta 12. ∫(tanx)/√(cosx) dx
Solución:
Dado que I = ∫(tanx)/√(cosx) dx
yo = ∫senx/cosx√(cosx) dx
= ∫ sinx/(cosx) 3/2 dx
= ∫senx/(cosx) 3/2 dx ……..(i)
Consideremos cosx = t entonces,
Al diferenciar ambos lados obtenemos,
d(cosx) = dt
-sinxdx = dt
senxdx = -dt
Ahora, al poner cosx = t y sinxdx = -dt en la ecuación (i), obtenemos
yo = ∫(-dt)/t -3/2
= -∫t -3/2 dt
= -[-2t -1/2 ] + c
= 2/t 1/2 + c
= 2/√(cosx) + c)
Por lo tanto, yo = 2/√(cosx) + c
Pregunta 13. ∫cos 3 x/√(senx) dx
Solución:
Dado que I = ∫cos 3 x/√(sinx) dx
= ∫(cos 2 xcosx)/√(senx) dx
= ∫((1 – sen 2 x)cosx)/√(senx) dx
= ∫((1 – sen 2 x))/√(senx) cosxdx ……(i)
Consideremos senx = t entonces,
Al diferenciar ambos lados obtenemos,
d(senx) = dt
cosxdx = dt
Ahora, al poner senx = t y cosxdx = dt en la ecuación (i), obtenemos
yo = ∫(1 – t 2 )/√t dt
= ∫(t -1/2 -t 2 xt -1/2 )dt
=∫(t -1/2 – t 3/2 )dt
= 2t 1/2 – 2/5 t 5/2 + c
= 2(senx) 1/2 – 2/5(senx) 5/2 + c
Por lo tanto, yo = 2√(sinx) – 2/5(sinx) 5/2 + c
Pregunta 14. ∫(sen 3 x)/√(cosx) dx
Solución :
Dado que I = ∫(sen 3 x)/√(cosx) dx
= ∫(sen 2 xsenx)/√(cosx) dx
=∫((1 – cos 2 x))/√(cosx) senxdx …….(i)
Consideremos cosx = t entonces,
Al diferenciar ambos lados obtenemos,
d(cosx) = dt
-sinxdx = dt
senxdx = -dt
Ahora, al poner cosx = t y sinxdx = -dt en la ecuación (i), obtenemos
yo = ∫((1 – t 2 ))/√t × -dt
= ∫(t 2 – 1)/√t dt
= ∫(t 2 /t 1/2 – 1/t 1/2 )dx
= ∫(t 2-1/2 – t -1/2 )dt
= ∫(t 3/2 – t 1/2 )dt
= 2/5 t 5/2 – 2t 1/2 + c
= 2/5 cos 5/2 x – 2 cos 1/2 x + c
Por lo tanto, I = 2/5 cos 5/2 x – 2√(cosx) + c
Pregunta 15. ∫1/(√(tan -1 x) (1 + x 2 )) dx
Solución:
Dado que I = ∫1/(√(tan -1 x) (1 + x 2 )) dx …..(i)
Consideremos tan -1 x = t, entonces
Al diferenciar ambos lados obtenemos,
d(tan -1 x) = dt
1/(1 + x 2 ) dx = dt
Ahora, al poner tan -1 x = t y 1/(1 + x 2 ) dx = dt en la ecuación (i), obtenemos
yo = ∫1/√t dt
= ∫t -1/2 dt
= 2t 1/2 + c
= 2√tan -1 x + c
Por lo tanto, yo = 2√tan -1 x + c
Pregunta 16. ∫√(tanx)/(senxcosx) dx
Solución:
Dado que I = ∫√(tanx)/(sinxcosx) dx
= ∫(√(tanx)×cosx)/(senxcosx×cosx) dx
= ∫√(tanx)/(tanxcos 2 x) dx
= ∫(seg 2 xdx)/√(bronceadox) dx
Consideremos tanx = t, entonces
Al diferenciar ambos lados obtenemos,
segundo 2 xdx = dt
Ahora
yo = ∫ dt/√t
= 2√t + c
Por lo tanto, yo = 2√tanx + c
Pregunta 17. 1/x × (logx) 2 dx
Solución:
Dado que I = ∫1/x × (logx) 2 dx …..(i)
Consideremos logx = t entonces,
Al diferenciar ambos lados obtenemos,
d(logx) = dt
1/x dx = dt
Ahora, al poner logx = t y 1/x dx = dt en la ecuación (i), obtenemos
yo = ∫t 2 dt
= t 3 /3 + c
= (logx) 3 /3 + c
Por lo tanto, yo = (logx) 3 /3 + c
Pregunta 18. ∫sen 5 x cosx dx
Solución:
Dado que I = ∫sen 5 x cosx dx ……(i)
Consideremos senx = t entonces,
Al diferenciar ambos lados obtenemos,
d(senx) = dt
cosxdx = dt
Ahora, al poner senx = t y cosxdx = dt en la ecuación (i), obtenemos
yo = ∫ t 5 dt
= t 6 /6 + c
= (sen 6 x)/6 + c
Por lo tantoc, I = 1/6 (sen 6 x) + c
Pregunta 19. ∫tan 3/2 x seg 2 x dx
Solución:
Dado que I = ∫tan 3/2 xsec 2 xdx ……(i)
Consideremos tanx = t entonces,
Al diferenciar ambos lados obtenemos,
d(tanx) = dt
segundo 2 xdx = dt
Ahora, al poner tanx = t y sec 2 xdx = dt en la ecuación (i), obtenemos
yo = ∫ t 3/2 dt
= 2/5 t 5/2 + c
= 2/5(tanx) 5/2 + c
Por lo tanto, I = 2/5 tan 5/2 x + c
Pregunta 20. ∫(x 3 )/(x 2 + 1) 2 dx
Solución:
Dado que I = ∫(x 3 )/(x 2 + 1) 2 dx …….(i)
Consideremos 1 + x 2 = t entonces,
Al diferenciar ambos lados obtenemos,
d(1 + x 2 ) = dt
2xdx = dt
xdx = dt/2
Ahora, al poner 1 + x 2 = t y xdx = dt/2 en la ecuación (i), obtenemos
yo = ∫x 2 /t 3 × dt/2
= 1/2∫(t – 1)/t 3 dt [1 + x 2 = t]
= 1/2∫[(t/t 3 – 1/t 3 )dt]
= 1/2∫(t -2 – t -3 )dt
= 1/2 [-1t -1 – t -2 /(-2)] + c
= 1/2 [-1/t + 1/(2t 2 )] + c
= -1/2t + 1/(4t 2 ) + c
= -1/2(1 + x 2 ) + 1/(4(1 + x 2 ) 2 ) + c
= (-2(1 + x 2 ) + 1)/(4(1 + x 2 ) 2 ) + c
= (-2 – 2x 2 + 1)/(4(1 + x 2 ) 2 ) + c
= (-2x 2 – 1)/(4(1 + x 2 ) 2 ) + c
= -(1 + 2x 2 )/(4(x 2 + 1) 2 ) + c
Henec, yo = -(1 + 2x 2 )/(4(x 2 + 1) 2 ) + c
Pregunta 21. ∫(4x + 2)√(x 2 + x + 1) dx
Solución:
Dado que I = ∫(4x + 2)√(x 2 + x + 1) dx
Consideremos x 2 + x + 1 = t entonces,
Al diferenciar ambos lados obtenemos,
(2x + 1)dx = dt
Ahora,
yo = ∫ (4x + 2)√(x 2 + x + 1) dx
= ∫2√t dt
= 2∫√t dt
= 2t 3/2 /(3/2) + c
Por tanto, yo = 4/3 (x 2 + x + 1) 3/2 + c
Pregunta 22. ∫(4x + 3)/√(2x 2 + 3x + 1) dx
Solución:
Dado que l = ∫(4x + 3)/√(2x 2 + 3x + 1) dx ……(i)
Consideremos 2x 2 + 3x + 1 = t entonces,
Al diferenciar ambos lados obtenemos,
d(2x 2 + 3x + 1) = dt
(4x + 3)dx = dt
Ahora al poner 2x 2 + 3x + 1 = t y (4x + 3)dx = dt en la ecuación (i), obtenemos
yo = ∫dt/√t
= ∫t -1/2 dt
= 2t 1/2 + c
= 2√t + c
Por lo tanto, yo = 2√(2x 2 + 3x + 1) + c
Pregunta 23. ∫1/(1 + √x) dx
Solución:
Dado que I = ∫1/(1 + √x) dx …….(i)
Consideremos x = t 2 entonces,
Al diferenciar ambos lados obtenemos,
dx = d(t 2 )
dx = 2tdt
Ahora, al poner x = t 2 y dx = 2tdt en la ecuación (i), obtenemos
yo = ∫2t/(1 + √(t 2 )) dt
= ∫2t/(1 + t) dt
= 2∫t/(1 + t) dt
= 2∫(1 + t – 1)/(1 + t) dt
= 2⌋[(1 + t)/(1 + t) – 1/(1 + t)]dt
= 2∫dt – 2∫1/(1 + t) dt
= 2t – 2log|(1 + t)| +c
= 2√x – 2log|(1 + √x)| +c
Por lo tanto, yo = 2√x – 2log|(1 + √x)| +c
Pregunta 24. 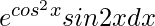
Solución:
Dado que I =
…….(i)
Consideremos cos 2 x = t entonces,
Al diferenciar ambos lados obtenemos,
d(cos 2 x) = dt
-2cosx senx dx = dt
-sin2x dx = dt
sin2x dx = -dt
Ahora al poner cos 2 x = t y sin2x dx = -dt en la ecuación (i), obtenemos
yo = ∫e t (-dt)
= -e t + c
= –
+ c
Por lo tanto, yo = –
+ c
Publicación traducida automáticamente
Artículo escrito por anandchaturvedirishra y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA