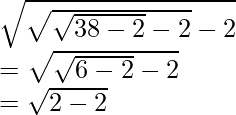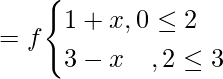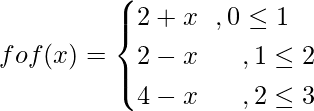Clase 12 RD Sharma Solutions – Capítulo 2 Funciones – Ejercicio 2.3

Pregunta 1. Encuentra niebla y gof, si

(i) f (x) = e ^x ,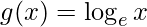 $g (x) = \log_ex$

Solución:

Sea f: R → (0, ∞); y g: (0, ∞) → R

Claramente, el rango de g es un subconjunto del dominio de f.

Entonces, niebla: (0, ∞) → R y sabemos, (niebla)(x) = f(g(x))

$= f(\log_ex)$

$= e^{log_ex}$

(niebla)(x) = x

Claramente, el rango de f es un subconjunto del dominio de g.

⇒ niebla: R→ R

(gof)(x) = g (f (x))

= g(e ^x )

$= log_ee^x$

(gof)(x) = x

(ii) f (x) = x ² , g(x) = cos x

Solución:

f: R→ [0, ∞) ; g: R→[−1, 1]

Claramente, el rango de g no es un subconjunto del dominio de f.

⇒ Dominio (niebla) = {x: x ∈ dominio de g y g (x) ∈ dominio de f}

⇒ Dominio (niebla) = x: x ∈ R y cos x ∈ R}

⇒ Dominio de (niebla) = R

(niebla): R→ R

(niebla)(x) = f (g(x))

= f(cosx)

(niebla)(x) = cos ² x

Claramente, el rango de f es un subconjunto del dominio de g.

⇒ niebla: R→R

(gof)(x) = g(f (x))

= gramo (x ² )

(gof)(x) = cos x ²

(iii) f(x) = |x|, g(x) = sen x

Solución:

f: R → (0, ∞) ; gramo: R→[−1, 1]

Claramente, el rango de g es un subconjunto del dominio de f.

⇒ niebla: R→R

(niebla)(x) = f (g (x))

= f (sen x)

(niebla)(x) = |sin x|

Claramente, el rango de f es un subconjunto del dominio de g.

⇒ niebla : R→ R

(gof)(x) = g (f (x))

= gramo (|x|)

(gof)(x) = sen |x|

(iv) f(x) = x + 1, g(x) = e ^x

Solución:

f: R→R; gramo: R → [ 1, ∞)

Claramente, el rango de g es un subconjunto del dominio de f.

⇒ niebla: R→R

(niebla)(x) = f (g (x))

= f(e ^x )

(niebla)(x) = e ^x + 1

Claramente, el rango de f es un subconjunto del dominio de g.

⇒ niebla: R→R

(gof)(x) = g(f (x))

= g(x+1)

(gof)(x) = e ^x +1

(v) f (x) = sen ⁻¹ x, g(x) = x ²

Solución:

f: [−1,1]→ [(-π)/2 ,π/2]; g : R → [0, ∞)

Dominio (niebla) = {x: x ∈ R y x ∈ [−1, 1]}

Entonces, Dominio de (niebla) = [−1, 1]

niebla: [−1,1] → R

(niebla)(x) = f (g (x))

= f( ^x2 )

(niebla)(x) = sen ⁻¹ (x ² )

Claramente, el rango de f es un subconjunto del dominio de g.

niebla: [−1, 1] → R

(gof)(x) = g (f (x))

= g (sen ⁻¹ x)

(gof)(x) = (sen ⁻¹ x) ²

(vi) f(x) = x+1, g(x) = senx

Solución:

f: R→R; g: R→[−1, 1]

Claramente, el rango de g es un subconjunto del dominio de f.

Conjunto del dominio de f.

⇒ niebla: R→ R

(niebla)(x) = f(g(x))

= f(senx)

(niebla)(x) = sen x + 1

Ahora tenemos que calcular gof,

Claramente, el rango de f es un subconjunto del dominio de g.

⇒ niebla: R → R

(gof)(x) = g (f (x))

= g(x+1)

(gof)(x) = sin(x+1)

(vii) f (x) = x+1, g (x) = 2x + 3

Solución:

f: R→R; g: R → R

Claramente, el rango de g es un subconjunto del dominio de f.

⇒ niebla: R→ R

(niebla)(x) = f (g (x))

= f(2x+3)

= 2x + 3 + 1

(niebla)(x) = 2x + 4

Claramente, el rango de f es un subconjunto del dominio de g.

⇒ niebla: R → R

(gof)(x) = g (f (x))

= gramo (x+1)

= 2 (x + 1) + 3

(gof)(x) = 2x + 5

(viii) f (x) = c, g (x) = sen x ²

Solución:

f: R → {c} ; gramo: R→ [ 0, 1 ]

Claramente, el rango de g es un subconjunto del dominio de f.

niebla: R→R

(niebla)(x) = f(g(x))

= f(senx ² )

(niebla)(x) = c

Claramente, el rango de f es un subconjunto del dominio de g.

⇒ niebla: R→ R

(gof)(x) = g (f (x))

= g(c)

(gof)(x) = sinc ²

(ix) f(x) = x ² + 2 y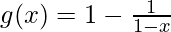 $g(x) = 1 - \frac{1}{1 - x}$

Solución:

f: R → [2, ∞)

Para el dominio de g: 1− x ≠ 0

⇒ X ≠ 1

⇒ Dominio de g = R − {1}

$g(x) = 1 - \frac{1}{1 - x}$

= $\frac{(1 - x - 1)}{(1 - x)}$

$= \frac{-x}{(1 - x)}$

Rango de g = R − {1}

Entonces, g: R − {1} → R − {1}

Claramente, el rango de g es un subconjunto del dominio de f.

⇒ niebla: R − {1} → R

(niebla) (x) = f (g (x))

$= f (\frac{-x}{1 - x})$

$(fog)(x) = (\frac{-x}{1 - x})^2 + 2$

Claramente, el rango de f es un subconjunto del dominio de g.

⇒ gof: R→R

(gof)(x) = g (f (x))

= g(x ² + 2)

$(gof)(x) = \frac{x^2 + 2}{x^2 + 1}$

Pregunta 2. Sea f(x) = x ² + x + 1 y g(x) = sen x. Muestre que niebla ≠ gof.

Solución:

Dado f(x) = x ² + x + 1 y g(x) = sen x

Ahora tenemos que probar niebla ≠ gof

(niebla)(x) = f(g(x))

= f(sen x)

(niebla)(x) = sen ² x + sen x + 1 …..(1)

Y (gof)(x) = g (f (x))

= gramo (x ² + x + 1)

(gof)(x) = sen (x2+ x + 1) ….(2)

De (1) y (2), obtenemos

niebla ≠ gof.

Pregunta 3. Si f(x) = |x|, demuestre que fof = f.

Solución:

Dado f(x) = |x|,

Ahora tenemos que demostrar que fof = f.

Considere (fof)(x) = f (f(x))

= f(|x|)

= ||x||

= |x|

= f(x)

Entonces, (fof) (x) = f (x), ∀x ∈ R

Por lo tanto, fof = f.

Pregunta 4. Si f(x) = 2x + 5 y g(x) = x ² + 1 son dos funciones reales, entonces describe cada una de las siguientes funciones:

(yo) niebla

Solución:

f(x) y g(x) son polinomios.

⇒ f: R → R y g: R → R.

Entonces, niebla: R → R y gof: R → R.

(i) (niebla) (x) = f (g (x))

= f (x ² + 1)

= 2 (x ² + 1) + 5

=2×2 ⁺ 2 + 5

= ^2×2 +7

(ii) gof

Solución:

(gof)(x) = g (f (x))

= gramo (2x +5)

= (2x + 5) ² + 1

= 4x ² + 20x + 26

(iii) de

Solución:

(fof)(x) = f (f (x))

= f (2x +5)

= 2 (2x + 5) + 5

= 4x + 10 + 5

= 4x + 15

(iv) f ² (x)

Solución:

f2 (x) ⁼ f(x) xf(x)

= (2x + 5)(2x + 5)

= (2x + 5) ²

= 4x ² + 20x +25

Pregunta 5. Si f(x) = sen x y g(x) = 2x son dos funciones reales, entonces describe gof y fog. ¿Son estas funciones iguales?

Solución:

Dado f(x) = sen x y g(x) = 2x

Lo sabemos

f: R→ [−1, 1] y g: R→ R

Claramente, el rango de f es un subconjunto del dominio de g.

gof: R→ R

(gof)(x) = g(f(x))

= g(sen x)

= 2 sen x

Claramente, el rango de g es un subconjunto del dominio de f.

niebla: R → R

Entonces, (niebla)(x) = f(g(x))

= f(2x)

= sen(2x)

Claramente, niebla ≠ gof

Por tanto, no son funciones iguales.

Pregunta 6. Sean f, g, h funciones reales dadas por f(x) = sen x, g(x) = 2x y h(x) = cos x. Demostrar que niebla = ir (fh).

Solución:

Dado que f(x) = sen x, g (x) = 2x y h (x) = cos x

Ahora, niebla(x) = f(g(x))

= f(2x)

niebla(x) = sen2x ….(1)

Y (ir (fh)) (x) = g ((f(x). h(x))

= g (sen x cos x)

= 2 sen x cos x

= sen (2x) ….(2)

De (1) y (2), fog(x) = go(fh) (x).

Pregunta 7. Sea f cualquier función real y sea g una función dada por g(x) = 2x. probar que: gof = f+f.

Solución:

Sabemos, (gof)(x) = g(f(x))

= 2(f(x))

= f(x) + f(x)

= f + f.

Por lo tanto probado.

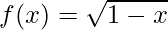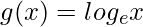Pregunta 8. Si $f(x) = \sqrt{1 - x}$ y $g(x) = log_ex$ son dos funciones reales, hallar fog y gof.

Solución:

Claramente el dominio de f y g son R.

Ahora, niebla(x) = f(g(x))

$= f(log_ex)$

niebla (x) $= \sqrt{1 - log_ex}$

(gof)(x) = g(f(x))

$= g(\sqrt{1 - x})$

(gof)(x) $= log_e\sqrt{1 - x}$

Pregunta 9. Si f(x) = tan x y 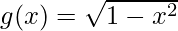$g(x) = \sqrt{1 - x^2}$ , encuentre niebla y gof.

Solución:

niebla(x) = f(g(x))

$= f(\sqrt{1 - x^2})$

$fog(x)= tan\sqrt{1 - x^2}$

(gof)(x) = g(f(x))

= g(tan x)

$(gof)(x) = \sqrt{1 - tan^2x}$

Pregunta 10. Si 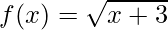$f(x) = \sqrt{x + 3}$ y g(x) = x ² + 1 son dos funciones reales, encuentre fog y gof.

Solución:

niebla(x) = f(g(x))

= f(x2 ⁺ 1)

$fog(x) = \sqrt{x^2 + 4}$

(gof)(x) = g(f(x))

$= g(\sqrt{x + 3})$

$= (\sqrt{x + 3})^2 + 1$

(gof)(x) = x + 4

Pregunta 11. Sea f una función real dada por $f(x) = \sqrt{x - 2}$ . Encontrar:

(i) de

Solución:

fof(x) = f(f(x))

$= f(\sqrt{x - 2})$

$fof(x) = \sqrt{\sqrt{x - 2} - 2}$

(ii) fofo

Solución:

Sabemos, fof(x) = f(f(x))

$= f(\sqrt{x - 2})$

De este modo, $fof(x) = \sqrt{\sqrt{x - 2} - 2}$

Ahora, fof(x) = fof(f(x))

$= fof(\sqrt{x - 2})$

$fofof(x) = \sqrt{\sqrt{\sqrt{x - 2} - 2} - 2}$

(iii) (foof) (38)

Solución:

Como se obtuvo de la parte anterior, tenemos

$fofof(x) = \sqrt{\sqrt{\sqrt{x - 2} - 2} - 2}$

Entonces obtenemos,

fofo (38) = $\sqrt{\sqrt{\sqrt{38 - 2} - 2} - 2}\\ =\sqrt{\sqrt{6 - 2} - 2}\\ =\sqrt{2 - 2}$

= 0

(iv) f ²

Solución:

f2 (x) = f(x).f(x ⁾

= $(\sqrt{x - 2})^2$

f2 ⁽ x) = x – 2

Pregunta 12. Sea 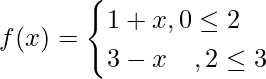$f(x)= \begin{cases}1+x,0\lex\le2\\3-x\ \ \ ,2\lex\le3\end{cases}$ fof.

Solución:

Rango de f = [0,3]

fof(x) = f(f(x))

$= f{\begin{cases}1+x,0\lex\le2\\3-x\ \ \ ,2\lex\le3\end{cases}}$

$fof(x) = \begin{cases}2+x\ \ ,0\lex\le1\\2-x\ \ \ \ \ ,1\lex\le2\\4-x\ \ \ \ \ ,2\lex\le3\end{cases}$

Pregunta 13. Si f, g : R → R son dos funciones definidas como f(x) = |x| + x y g(x) = |x|- x, ∀ x∈R. Luego encuentra niebla y gof. Por lo tanto, encuentre fog(–3), fog(5) y gof (–2).

Solución:

Se da que, f(x) = |x| + x y g(x) = |x| -x, ∀x ∈ R

niebla = f(g(x)) = | gramo (x) | + g(x)

= ||x| − x| + (|x| − x)

gof = g (f(x)) = |f(x)| − f(x)

= ||x| + x| − (|x| + x)

Entonces, g (f(x)) = gof = 0

Ahora, fog(−3) =(4)(−3) = −12, como fog = 4x para x < 0

niebla (5) = 0, como niebla = 0 para x ≥ 0

gof(−2) = 0, como gof = 0 para x < 0

Publicación traducida automáticamente

Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Encuentra niebla y gof, si

(i) f (x) = e x ,

(ii) f (x) = x 2 , g(x) = cos x

(iii) f(x) = |x|, g(x) = sen x

(iv) f(x) = x + 1, g(x) = e x

(v) f (x) = sen −1 x, g(x) = x 2

(vi) f(x) = x+1, g(x) = senx

(vii) f (x) = x+1, g (x) = 2x + 3

(viii) f (x) = c, g (x) = sen x 2

(ix) f(x) = x 2 + 2 y

Pregunta 2. Sea f(x) = x 2 + x + 1 y g(x) = sen x. Muestre que niebla ≠ gof.

Pregunta 3. Si f(x) = |x|, demuestre que fof = f.

Pregunta 4. Si f(x) = 2x + 5 y g(x) = x 2 + 1 son dos funciones reales, entonces describe cada una de las siguientes funciones:

Pregunta 5. Si f(x) = sen x y g(x) = 2x son dos funciones reales, entonces describe gof y fog. ¿Son estas funciones iguales?

Pregunta 6. Sean f, g, h funciones reales dadas por f(x) = sen x, g(x) = 2x y h(x) = cos x. Demostrar que niebla = ir (fh).

Pregunta 7. Sea f cualquier función real y sea g una función dada por g(x) = 2x. probar que: gof = f+f.

Pregunta 8. Si y son dos funciones reales, hallar fog y gof.

Pregunta 9. Si f(x) = tan x y , encuentre niebla y gof.

Pregunta 10. Si y g(x) = x 2 + 1 son dos funciones reales, encuentre fog y gof.

Pregunta 11. Sea f una función real dada por . Encontrar:

(i) de

(ii) fofo

(iii) (foof) (38)

(iv) f 2

Pregunta 12. Sea fof.

Pregunta 13. Si f, g : R → R son dos funciones definidas como f(x) = |x| + x y g(x) = |x|- x, ∀ x∈R. Luego encuentra niebla y gof. Por lo tanto, encuentre fog(–3), fog(5) y gof (–2).

Deja una respuesta Cancelar la respuesta

(i) f (x) = e ^x , $g (x) = \log_ex$

(ii) f (x) = x ² , g(x) = cos x

(iv) f(x) = x + 1, g(x) = e ^x

(v) f (x) = sen ⁻¹ x, g(x) = x ²

(viii) f (x) = c, g (x) = sen x ²

(ix) f(x) = x ² + 2 y $g(x) = 1 - \frac{1}{1 - x}$

Pregunta 2. Sea f(x) = x ² + x + 1 y g(x) = sen x. Muestre que niebla ≠ gof.

Pregunta 4. Si f(x) = 2x + 5 y g(x) = x ² + 1 son dos funciones reales, entonces describe cada una de las siguientes funciones:

Pregunta 8. Si $f(x) = \sqrt{1 - x}$ y $g(x) = log_ex$ son dos funciones reales, hallar fog y gof.

Pregunta 9. Si f(x) = tan x y $g(x) = \sqrt{1 - x^2}$ , encuentre niebla y gof.

Pregunta 10. Si $f(x) = \sqrt{x + 3}$ y g(x) = x ² + 1 son dos funciones reales, encuentre fog y gof.

Pregunta 11. Sea f una función real dada por $f(x) = \sqrt{x - 2}$ . Encontrar:

(iv) f ²

Pregunta 12. Sea $f(x)= \begin{cases}1+x,0\lex\le2\\3-x\ \ \ ,2\lex\le3\end{cases}$ fof.