Evalúe las siguientes integrales definidas:
Pregunta 1. 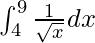
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo = 2[√9 – √4]
yo = 2 (3 − 2)
yo = 2 (1)
yo = 2
Por lo tanto, el valor de
es 2.
Pregunta 2. 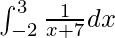
Solución:
Tenemos,
yo =
yo =
yo = logaritmo (3 + 7) − logaritmo (−2 + 7)
I = logaritmo 10 − logaritmo 5
yo =
yo = registro 2
Por lo tanto, el valor de
es log 2.
Pregunta 3. 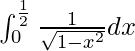
Solución:
Tenemos,
yo =
Sea x = sen t, entonces tenemos,
=> dx = cos t dt
Ahora, el límite inferior es,
=> x = 0
=> sen t = 0
=> t = 0
Además, el límite superior es,
=> x = 1/2
=> sen t = 1/2
=> t = π/6
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
yo = /6 – 0
yo = /6
Por lo tanto, el valor de
es π/6.
Pregunta 4. 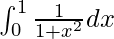
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo = π/4
Por lo tanto, el valor de
es π/4.
Pregunta 5. 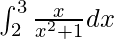
Solución:
Tenemos,
yo =
Sea x 2 + 1 = t, entonces tenemos,
=> 2x dx = dt
=> x dx = dt/2
Ahora, el límite inferior es, x = 2
=> t = x2 + 1
=> t = (2) 2 + 1
=> t = 4 + 1
=> t = 5
Además, el límite superior es, x = 3
=> t = x2 + 1
=> t = (3) 2 + 1
=> t = 9 + 1
=> t = 10
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo = 1/2[log10 – log5]
yo = 1/2[log10/5]
yo = 1/2[log2]
yo = log√2
Por lo tanto, el valor de
es log√2.
Pregunta 6. 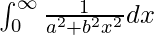
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
yo = 1/ab[tan -1 ∞ – tan -1 0]
yo = 1/ab[π/2 – 0]
yo = 1/ab[π/2]
yo = π/2ab
Por lo tanto, el valor de
es π/2ab.
Pregunta 7. 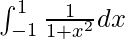
Solución:
Tenemos,
yo =
yo =
yo = [tan -1 1 – tan -1 (-1)]
yo = [π/4 – (-π/4)]
yo = [π/4 + π/4]
yo = 2π/4
yo = π/2
Por lo tanto, el valor de
es π/2.
pregunta 8 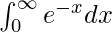
Solución:
Tenemos,
yo =
yo =
yo = -e-
yo = − 0 + 1
yo = 1
Por lo tanto, el valor de
es 1.
Pregunta 9. 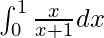
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
yo = [1 − 0] − [log(1 + 1) − log(0 + 1)]
yo = 1 − [log2 − log1]
I = 1 – log2/1
yo = 1 − registro 2
yo = log e − log 2
I = loge/2
Por lo tanto, el valor de
es loge/2.
Pregunta 10. 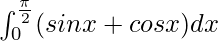
Solución:
Tenemos,
yo =
yo =
yo =
I = [-cosπ/2 + cos0] + [senπ/2 – sin0]
yo = [−0 + 1] + 1
yo = 1 + 1
yo = 2
Por lo tanto, el valor de
es 2.
Pregunta 11. 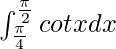
Solución:
Tenemos,
yo =
yo =
I = log(senπ/2) – log(senπ/4)
Yo = log1 – log1/√2
yo =
yo = log√2
Por lo tanto, el valor de
es log√2.
Pregunta 12. 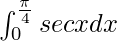
Solución:
Tenemos,
yo =
yo =
I = log(secπ/4 + tanπ/4 – log(sec0 + tan0)
I = logaritmo(√2 + 1) – logaritmo(1 + 0)
yo =
yo = logaritmo(√2 + 1)
Por lo tanto, el valor de
es log(√2 + 1).
Pregunta 13. 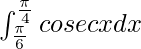
Solución:
Tenemos,
yo =
yo =
I = [log|cosecπ/4 – cotπ/4|] – [log|cosecπ/6 – cotπ/6|]
yo = [log|√2 – 1|] – [log|2 – √3|]
yo =
Por lo tanto, el valor de
es
.
Pregunta 14. 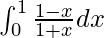
Solución:
Tenemos,
yo =
Sea x = cos 2t, entonces tenemos,
=> dx = –2 sen 2t dt
Ahora, el límite inferior es,
=> x = 0
=> porque 2t = 0
=> 2t = π/2
=> t = π/4
Además, el límite superior es,
=> x = 1
=> porque 2t = 1
=> 2t = 0
=> t = 0
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
Sea cos t = z, entonces tenemos,
=> – sen t dt = dz
=> sen t dt = – dz
Ahora, el límite inferior es,
=> t = 0
=> z = cos t
=> z = cos 0
=> z = 1
Además, el límite superior es,
=> t = π/4
=> z = cos t
=> z = cos π/4
=> z = 1/√2
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
yo =
Yo = -4[(log1/√2 – 1/2(2)) – (log1 – 1/2)]
Yo = -4[(log1/√2 – 1/4) – (0 – 1/2)]
Yo = -4[log1/√2 – 1/4 – 0 + 1/2]
Yo = -4[-log√2 + 1/4]
Yo = 4log√2 – 1
yo = 4 × 1/2log2 – 1
yo = 2log2 – 1
Por lo tanto, el valor de
es 2log2 – 1.
Pregunta 15. 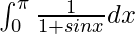
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
I = [tan π – tan0] – [seg π – seg 0]
Yo = [0 – 0] – [–1 – 1]
Yo = 0 – (–2)
yo = 2
Por lo tanto, el valor de
es 2.
Pregunta 16. 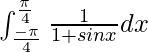
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
I = [tan π/4 – tan(–π/4)] – [seg π/4 – seg (–π/4)]
I = [1 – (–1)] – [seg π/4 – seg (π/4)]
yo = 2 – 0
yo = 2
Por lo tanto, el valor de
es 2.
Pregunta 17. 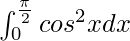
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
yo =
yo = 1/2[π/2 – 0] + 1/4[senπ – sin0]
Yo = 1/2[π/2] + 1/4[0 – 0]
yo = π/4
Por lo tanto, el valor de
es π/4 .
Pregunta 18. 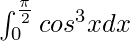
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
yo =
Yo = 1/12 [-1 – 0] + 3/4 [1 – 0]
yo = 3/4 – 1/12
yo = (9 – 1)/12
yo = 8/12
yo = 2/3
Por lo tanto, el valor de
es 2/3.
Pregunta 19. 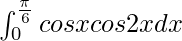
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
yo =
I = 1/6[senπ/2 – sin0] + 1/2[senπ/6 – sin0]
Yo = 1/6[1 – 0] + 1/2[1/2 – 0]
yo = 1/6 + 1/4
yo = (4 + 6)/24
yo = 10/24
yo = 5/12
Por lo tanto, el valor de
es 5/12 .
Pregunta 20. 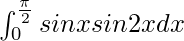
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
yo =
I = 1/2[sinπ/2 – sin0] – 1/6[sin3π/2 – sin0]
Yo = 1/2[1 – 0] – 1/6[-1 – 0]
Yo = 1/2 – 1/6(-1)
yo = 1/2 + 1/6
yo = (6 + 2)/12
yo = 8/12
yo = 2/3
Por lo tanto, el valor de
es 2/3.
Pregunta 21. 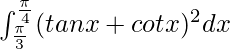
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
I = 2[-cotπ/2 + cot2π/3]
Yo = 2[-1/√3 – 0]
Yo = -2/√3
Por lo tanto, el valor de
es -2/√3.
Pregunta 22. 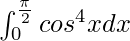
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo = 1/4[π/2 + π/4 + 0 + 0 – 0 – 0 – 0 – 0]
yo = 1/4[3π/4]
yo = 3π/16
Por lo tanto, el valor de
es 3π/16 .
Publicación traducida automáticamente
Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
![Rendered by QuickLaTeX.com \left[\frac{x^{\frac{-1}{2}+1}}{\frac{-1}{2}+1}\right]^9_4](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-02b35b8e26df515cfadbc6b0f4052d5b_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{x^{\frac{1}{2}}}{\frac{1}{2}}\right]^9_4](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b290aa2a3292080c88433221803b31cc_l3.png)
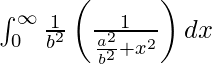
![Rendered by QuickLaTeX.com -4\left[logz-\frac{z^2}{2}\right]^{\frac{1}{\sqrt{2}}}_1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7d85750d6b98e18a00af99aee3d4d8fc_l3.png)
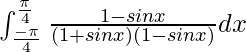
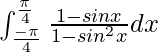
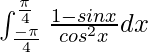
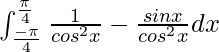
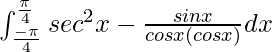
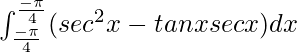
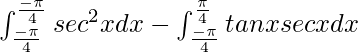
![Rendered by QuickLaTeX.com \left[tanx\right]^{\frac{\pi}{4}}_{\frac{-\pi}{4}}-\left[secx\right]^{\frac{\pi}{4}}_{\frac{-\pi}{4}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0d76195c0a49c58bca6055ab7537bdb2_l3.png)