Evalúe las siguientes integrales definidas:
Pregunta 21. 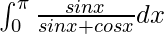
Solución:
Tenemos,
yo =
Sea sen x = A (sen x + cos x) + B
=> sen x = A (sen x + cos x) + B (cos x – sen x)
=> sen x = sen x (A – B) + cos x (A + B)
Al comparar ambos lados, obtenemos
A – B = 1 y A + B = 0
Al resolver obtenemos A = 1/2 y B = –1/2.
Por lo tanto, la expresión se convierte en,
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 22. 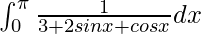
Solución:
Tenemos,
yo =
Al poner cos x =
y sen x =
, obtenemos,
yo =
yo =
yo =
yo =
Sea tan x/2 = t. Entonces tenemos
=> 1/2 seg 2 x/2 dx = dt
=> seg 2 x/2 dx = 2 dt
Ahora, el límite inferior es, x = 0
=> t = tan x/2
=> t = tan 0/2
=> t = bronceado 0
=> t = 0
Además, el límite superior es, x = π
=> t = tan x/2
=> t = tan π/2
=> t = ∞
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 23. 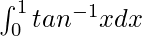
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 24. 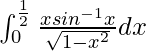
Solución:
Tenemos,
yo =
Sea sen –1 x = t. Entonces tenemos
=>
= dt
Ahora, el límite inferior es, x = 0
=> t = sen –1 x
=> t = sen –1 0
=> t = 0
Además, el límite superior es, x = 1/2
=> t = sen –1 x
=> t = sen –1 1/2
=> t = π/6
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 25. 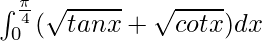
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
Sea senx – cosx = t. Entonces tenemos
=> (cos x + sen x) dx = dt
Ahora, el límite inferior es, x = 0
=> t = senx – cosx
=> t = sen 0 – cos 0
=> t = 0 – 1
=> t = –1
Además, el límite superior es, x = π/4
=> t = senx – cosx
=> t = sen π/4 – cos π/4
=> t = sen π/4 – sen π/4
=> t = 0
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 26. 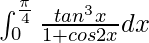
Solución:
Tenemos,
yo =
yo =
yo =
yo =
Sea tan x = t. Entonces tenemos
=> seg 2 x dx = dt
Ahora, el límite inferior es, x = 0
=> t = bronceado x
=> t = bronceado 0
=> t = 0
Además, el límite superior es, x = π/4
=> t = bronceado x
=> t = tan π/4
=> t = 1
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 27. 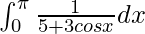
Solución:
Tenemos,
yo =
Al poner cos x =
, obtenemos
yo =
yo =
yo =
Sea tan x/2 = t. Entonces tenemos
=> 1/2 seg 2 x/2 dx = dt
=> seg 2 x/2 dx = 2 dt
Ahora, el límite inferior es, x = 0
=> t = tan x/2
=> t = tan 0/2
=> t = bronceado 0
=> t = 0
Además, el límite superior es, x = π
=> t = tan x/2
=> t = tan π/2
=> t = ∞
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 28. 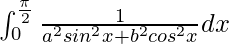
Solución:
Tenemos,
yo =
yo =
yo =
yo =
Sea tan x = t. Entonces tenemos
=> seg 2 x dx = dt
Ahora, el límite inferior es, x = 0
=> t = bronceado x
=> t = bronceado 0
=> t = 0
Además, el límite superior es, x = π/2
=> t = bronceado x
=> t = tan π/2
=> t = ∞
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 29. 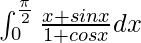
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 30. 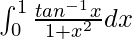
Solución:
Tenemos,
yo =
Sea tan –1 x = t. Entonces tenemos
=>
= dt
Ahora, el límite inferior es, x = 0
=> t = bronceado –1 x
=> t = bronceado –1 0
=> t = 0
Además, el límite superior es, x = 1
=> t = bronceado –1 x
=> t = bronceado –1 1
=> t = π/4
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 31. 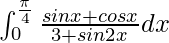
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 32. 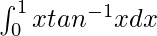
Solución:
Tenemos,
yo =
Al usar la integración por partes, obtenemos
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 33. 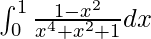
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 34. 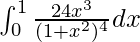
Solución:
Tenemos,
yo =
Sea 1 + x 2 = t. Entonces tenemos
=> 2x dx = dt
Ahora, el límite inferior es, x = 0
=> t = 1 + x 2
=> t = 1 + 0 2
=> t = 1 + 0
=> t = 1
Además, el límite superior es, x = π
=> t = 1 + x 2
=> t = 1 + 1 2
=> t = 1 + 1
=> t = 2
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo = 1
Por lo tanto, el valor de
es 1.
Pregunta 35. 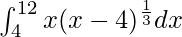
Solución:
Tenemos,
yo =
Sea x – 4 = t 3 . Entonces tenemos
=> dx = 3t 2 dt
Ahora, el límite inferior es, x = 4
=> t 3 = x – 4
=> t 3 = 4 – 4
=> t 3 = 0
=> t = 0
Además, el límite superior es, x = 12
=> t 3 = x – 4
=> t 3 = 12 – 4
=> t 3 = 8
=> t = 2
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 36. 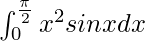
Solución:
Tenemos,
yo =
Al usar la integración por partes, obtenemos
yo =
yo =
yo =
yo =
yo =
yo = π + 0 – 0 – 0 – 2
yo = π – 2
Por lo tanto, el valor de
es π – 2.
Pregunta 37. 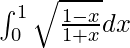
Solución:
Tenemos,
yo =
Sea x = cos 2t. Entonces tenemos
=> dx = – 2 sen 2t dt
Ahora, el límite inferior es, x = 0
=> cos 2t = x
=> porque 2t = 0
=> 2t = π/2
=> t = π/4
Además, el límite superior es, x = 1
=> cos 2t = x
=> porque 2t = 1
=> 2t = 0
=> t = 0
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 38. 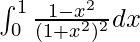
Solución:
Tenemos,
yo =
yo =
yo =
Sea x + 1/x = t. Entonces tenemos
=> (1 – 1/x 2 )dx = dt
Ahora, el límite inferior es, x = 0
=> t = x + 1/x
=> t = ∞
Además, el límite superior es, x = 1
=> t = x + 1/x
=> t = 1 + 1
=> t = 2
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 39. 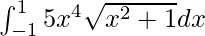
Solución:
Tenemos,
yo =
Sea x 5 + 1 = t. Entonces tenemos
=> 5x 4 dx = dt
Ahora, el límite inferior es, x = –1
=> t = x 5 + 1
=> t = (–1) 5 + 1
=> t = –1 + 1
=> t = 0
Además, el límite superior es, x = 1
=> t = x 5 + 1
=> t = (1) 5 + 1
=> t = 1 + 1
=> t = 2
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 40. 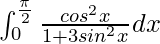
Solución:
Tenemos,
yo =
yo =
Sea tan x = t. Entonces tenemos
=> seg 2 x dx = dt
Ahora, el límite inferior es, x = 0
=> t = bronceado x
=> t = bronceado 0
=> t = 0
Además, el límite superior es, x = π/2
=> t = bronceado x
=> t = tan π/2
=> t = ∞
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 41. 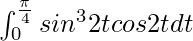
Solución:
Tenemos,
yo =
Sea sen 2t = u. Entonces tenemos
=> 2 cos 2t dt = du
=> cos 2t dt = du/2
Ahora, el límite inferior es, x = 0
=> u = sen 2t
=> u = sen 0
=> tu = 0
Además, el límite superior es, x = π/4
=> u = sen 2t
=> u = sen π/2
=> tu = 1
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Publicación traducida automáticamente
Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
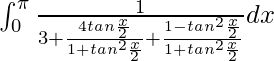
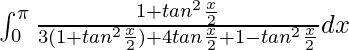
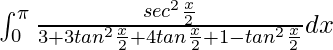
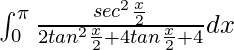
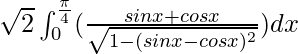
![Rendered by QuickLaTeX.com \frac{1}{2}\left[\frac{t^4}{4}\right]_{0}^{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5b523dd76a0034a3c23d8ffe48b7fe74_l3.png)
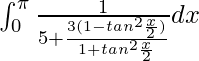
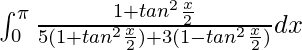
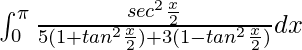
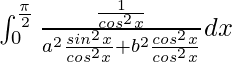
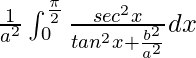
![Rendered by QuickLaTeX.com \left[xtan\frac{x}{2}-\int_{0}^{\frac{\pi}{2}}tan\frac{x}{2}dx+\int_{0}^{\frac{\pi}{2}}tan\frac{x}{2}dx\right]^{\frac{\pi}{2}}_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-52ea5a5994f4fae1034cc5e8a661812e_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{t^2}{2}\right]_{0}^{\frac{\pi}{4}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-41bf1dbb85d90b4ddf9fdae996e95d2a_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{1}{4}log|\frac{2+sinx-cosx}{2-sinx+cosx}|\right]_{0}^{\frac{\pi}{4}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3c9c9f5744510793d62e3fd90e340cac_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{x^2tan^{-1}x}{2}\right]_{0}^{1}-\frac{1}{2}\int_0^1\frac{x^2}{1+x^2}dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e5ad5a884573bcca405da5b00e643d45_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{x^2tan^{-1}x}{2}\right]_{0}^{1}-\frac{1}{2}\int_0^1\frac{1+x^2-1}{1+x^2}dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e379ad59b4504a54e8d2994b223e3b4a_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{x^2tan^{-1}x}{2}\right]_{0}^{1}-\frac{1}{2}\int_0^1\frac{1+x^2}{1+x^2}dx+\frac{1}{2}\int_0^1\frac{1}{1+x^2}dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-25504336990fd491983660f8d864f44f_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{x^2tan^{-1}x}{2}\right]_{0}^{1}-\frac{1}{2}\int_0^1dx+\frac{1}{2}\int_0^1\frac{1}{1+x^2}dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0318f3bd2c10a15a84b10009b2913d7a_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{x^2tan^{-1}x}{2}\right]_{0}^{1}-\frac{1}{2}\left[x\right]_0^1+\frac{1}{2}\left[tan^{-1}x\right]_0^1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-efbac77c0432844db5e99575d1c237f6_l3.png)
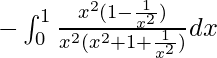
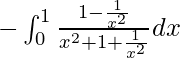
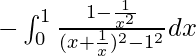
![Rendered by QuickLaTeX.com -\left[\frac{1}{2}\log|\frac{x+\frac{1}{x}-1}{x+\frac{1}{x}+1}|\right]^1_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f0cda8830c7239b929cdb2623b397f8c_l3.png)
![Rendered by QuickLaTeX.com -\left[\frac{1}{2}\log|\frac{x^2-x+1}{x^2+x+1}|\right]^1_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cdbe08c26b7db53d961c079487b5043c_l3.png)
![Rendered by QuickLaTeX.com 3\left[\frac{t^7}{7}+t^4\right]_{0}^{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c16512d9ae43744d2391601256185c5f_l3.png)
![Rendered by QuickLaTeX.com 2\left[t-\frac{sin^2t}{2}\right]^{\frac{\pi}{4}}_{0}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dd6aa1bbbaba469a20fb7604a33e5e66_l3.png)
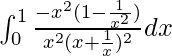
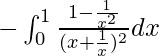
![Rendered by QuickLaTeX.com \left[\frac{2}{3}t^{\frac{3}{2}}\right]_{0}^{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-956089bf0bd15b42d1600f47ffb12c58_l3.png)
![Rendered by QuickLaTeX.com \frac{1}{2}\left[\frac{u^4}{4}\right]_{0}^{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e8af27d7948aebde5468385814a36efc_l3.png)