Evalúe las siguientes integrales definidas:
Pregunta 42. 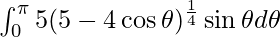
Solución:
Tenemos,
yo =
Sea 5 – 4 cos θ = t. Entonces tenemos
=> 4 sen θ dθ = dt
=> sen θ dθ = dt/4
Ahora, el límite inferior es, θ = 0
=> t = 5 – 4 cos θ
=> t = 5 – 4 cos 0
=> t = 5 – 4
=> t = 1
Además, el límite superior es, θ = π
=> t = 5 – 4 cos θ
=> t = 5 – 4 cos π
=> t = 5 + 4
=> t = 9
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo = 9√3 – 1
Por lo tanto, el valor de
es 9√3 – 1.
Pregunta 43. 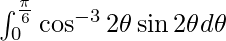
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
Sea tan 2θ = t. Entonces tenemos
=> 2 seg 2 2θ dθ = dt
=> seg 2 2θ dθ = dt/2
Ahora, el límite inferior es, θ = 0
=> t = tan 2θ
=> t = bronceado 0
=> t = 0
Además, el límite superior es, θ = π/6
=> t = tan 2θ
=> t = tan π/3
=> t = √3
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 44. 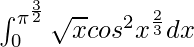
Solución:
Tenemos,
yo =
Sea
= t. Entonces tenemos
=>
= dt
Ahora, el límite inferior es, x = 0
=> t =
=> t =
=> t = 0
Además, el límite superior es, x =
=> t =
=> t =
=> t = π
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 45. 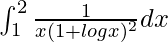
Solución:
Tenemos,
yo =
Sea 1 + log x = t. Entonces tenemos
=> 1/x dx = dt
Ahora, el límite inferior es, x = 0
=> t = 1 + registro x
=> t = 1 + registro 0
=> t = 1
Además, el límite superior es, x = 2
=> t = 1 + registro x
=> t = 1 + registro 2
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 46. 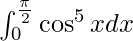
Solución:
Tenemos,
yo =
yo =
Sea sen x = t. Entonces tenemos
=> cos x dx = dt
Ahora, el límite inferior es, x = 0
=> t = sen x
=> t = sen 0
=> t = 0
Además, el límite superior es, x = π/2
=> t = sen x
=> t = sen π/2
=> t = 1
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 47. 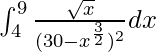
Solución:
Tenemos,
yo =
Sea 30 – x 3/2 = t. Entonces tenemos
=>
= dt
=>
= – dt
Ahora, el límite inferior es, x = 4
=> t = 30 – x 3/2
=> t = 30 – 4 3/2
=> t = 30 – 8
=> t = 22
Además, el límite superior es, x = 9
=> t = 30 – x 3/2
=> t = 30 – 9 3/2
=> t = 30 – 27
=> t = 3
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 48. 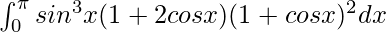
Solución:
Tenemos,
yo =
Sea cos x = t. Entonces tenemos
=> – sen x dx = dt
=> sen x dx = –dt
Ahora, el límite inferior es, x = 0
=> t = cos x
=> t = cos 0
=> t = 1
Además, el límite superior es, x = π
=> t = cos x
=> t = cos π
=> t = –1
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 49. 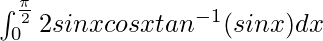
Solución:
Tenemos,
yo =
Sea sen x = t. Entonces tenemos
=> cos x dx = dt
Ahora, el límite inferior es, x = 0
=> t = sen x
=> t = sen 0
=> t = 0
Además, el límite superior es, x = π/2
=> t = sen x
=> t = sen π/2
=> t = 1
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 50. 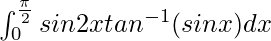
Solución:
Tenemos,
yo =
yo =
Sea sen x = t. Entonces tenemos
=> cos x dx = dt
Ahora, el límite inferior es, x = 0
=> t = sen x
=> t = sen 0
=> t = 0
Además, el límite superior es, x = π/2
=> t = sen x
=> t = sen π/2
=> t = 1
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 51. 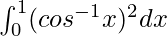
Solución:
Tenemos,
yo =
Al usar la integración por partes, obtenemos,
yo =
yo =
Sea cos -1 x = t. Entonces tenemos
=>
= dt
Ahora, el límite inferior es, x = 0
=> t = cos -1 x
=> t = cos -1 0
=> t = π/2
Además, el límite superior es, x = 1
=> t = cos -1 x
=> t = cos -1 1
=> t = 0
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo = π – 2
Por lo tanto, el valor de
es π – 2.
Pregunta 52. 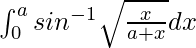
Solución:
Tenemos,
yo =
Sea x = a tan 2 t. Entonces tenemos
=> dx = 2a tan t seg 2 t dt
Ahora, el límite inferior es, x = 0
=> un bronceado 2 t = x
=> un bronceado 2 t = 0
=> bronceado t = 0
=> t = 0
Además, el límite superior es, x = a
=> un bronceado 2 t = x
=> un bronceado 2 t = un
=> bronceado 2 t = 1
=> bronceado t = 1
=> t = π/4
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 53. 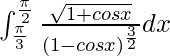
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
Sea cot x/2 = t. Entonces tenemos
=>
= dt
Ahora, el límite inferior es, x = π/3
=> t = cuna x/2
=> t = cuna π/6
=> t = √3
Además, el límite superior es, x = π/2
=> t = cuna x/2
=> t = cuna π/4
=> t = 1
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo = 1
Por lo tanto, el valor de
es 1.
Pregunta 54. 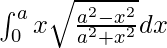
Solución:
Tenemos,
yo =
Sea x 2 = a 2 cos 2t. Entonces tenemos
=> 2x dx = – 2a 2 sen 2t dt
Ahora, el límite inferior es, x = 0
=> a 2 cos 2t = x 2
=> a 2 cos 2t = 0
=> porque 2t = 0
=> 2t = π/2
=> t = π/4
Además, el límite superior es, x = a
=> a 2 cos 2t = x 2
=> a 2 cos 2t = a 2
=> porque 2t = 1
=> 2t = 0
=> t = 0
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 55. 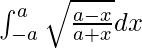
Solución:
Tenemos,
yo =
Sea x = a cos 2t. Entonces tenemos
=> dx = –2a sen 2t
Ahora, el límite inferior es, x = –a
=> a cos 2t = x
=> a cos 2t = –a
=> cos 2t = –1
=> 2t = π
=> t = π/2
Además, el límite superior es, x = a
=> a cos 2t = x
=> a cos 2t = a
=> porque 2t = 1
=> 2t = 0
=> t = 0
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo = πa
Por lo tanto, el valor de
es πa.
Pregunta 56. 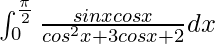
Solución:
Tenemos,
yo =
Sea cos x = t. Entonces tenemos
=> – sen x dx = dt
=> sen x dx = –dt
Ahora, el límite inferior es, x = 0
=> t = cos x
=> t = cos 0
=> t = 1
Además, el límite superior es, x = π/2
=> t = cos x
=> t = cos π/2
=> t = 0
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
I = – log 2 + 2 log 3 + 0 – 2 log 2
I = 2 log 3 – 3 log 2
I = registro 9 – registro 8
I = registro 9/8
Por lo tanto, el valor de
es log 9/8.
Pregunta 57. 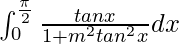
Solución:
Tenemos,
yo =
yo =
yo =
Sea sen 2 x = t. Entonces tenemos
=> 2 sen x cos x dx = dt
Ahora, el límite inferior es, x = 0
=> t = sen 2 x
=> t = sen 2 0
=> t = 0
Además, el límite superior es, x = π/2
=> t = sen 2 x
=> t = sen 2 π/2
=> t = 1
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 58. 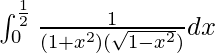
Solución:
Tenemos,
yo =
Sea x = sen t. Entonces tenemos
=> dx = cos t dt
Ahora, el límite inferior es, x = 0
=> sen t = x
=> sen t = 0
=> t = 0
Además, el límite superior es, x = 1/2
=> sen t = x
=> sen t = 1/2
=> t = π/6
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
Sea tan t = u. Entonces tenemos
=> seg 2 t dt = du
Ahora, el límite inferior es, t = 0
=> tu = bronceado t
=> tu = bronceado 0
=> t = 0
Además, el límite superior es, t = π/6
=> tu = bronceado t
=> u = tan π/6
=> t = 1/√3
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 59. 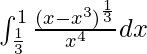
Solución:
Tenemos,
yo =
Sea 1/x 2 – 1 = t. Entonces tenemos
=> –2/x 3 dx = dt
Ahora, el límite inferior es, x = 1/3
=> t = 1/x 2 – 1
=> t = 9 – 1
=> t = 8
Además, el límite superior es, x = 1
=> t = 1/x 2 – 1
=> t = 1 – 1
=> t = 0
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
yo = 6
Por lo tanto, el valor de
es 6.
Pregunta 60. 
Solución:
Tenemos,
yo =
yo =
Sea tan x = t. Entonces tenemos
=> seg 2 x dx = dt
Ahora, el límite inferior es, x = 0
=> t = bronceado t
=> t = bronceado 0
=> t = 0
Además, el límite superior es, x = π/4
=> t = bronceado t
=> t = tan π/4
=> t = 1
Entonces, la ecuación se convierte en,
yo =
Sea t 3 = u. Entonces tenemos
=> 3t 2 dt = du
=> t 2 dt = du/3
Ahora, el límite inferior es, t = 0
=> tu = t 3
=> tu = 0 3
=> tu = 0
Además, el límite superior es, t = 1
=> tu = t 3
=> tu = 1 3
=> tu = 1
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 61. 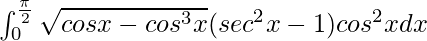
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
Sea cos x = t. Entonces tenemos
=> – sen x dx = dt
Ahora, el límite inferior es, x = 0
=> t = cos x
=> t = cos 0
=> t = 1
Además, el límite superior es, x = π/2
=> t = cos x
=> t = cos π/2
=> t = 0
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 62. 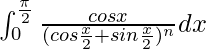
Solución:
Tenemos,
yo =
yo =
yo =
Sea cos x/2 + sen x/2 = t. Entonces tenemos
=> (cos x/2 – sen x/2) dx = 2 dt
Ahora, el límite inferior es, x = 0
=> t = cos x/2 + sen x/2
=> t = cos 0 + sen 0
=> t = 1 + 0
=> t = 1
Además, el límite superior es, x = π/2
=> t = cos x/2 + sen x/2
=> t = cos π/2 + sen π/2
=> t = 1/√2 + 1/√2
=> t = √2
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Publicación traducida automáticamente
Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
![Rendered by QuickLaTeX.com \frac{5}{4}\left[\frac{t^{\frac{5}{4}}}{\frac{5}{4}}\right]_{1}^{9}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f1e5b2ca2e3ed3842d648126b276a3ba_l3.png)
![Rendered by QuickLaTeX.com \frac{5}{4}\left[\frac{4}{5}t^{\frac{5}{4}}\right]_{1}^{9}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-507a704c3a9f061b6d718a6e47a24862_l3.png)
![Rendered by QuickLaTeX.com \left[t^{\frac{5}{4}}\right]_{1}^{9}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f1bc859be7d7153da05889b7109443fb_l3.png)
![Rendered by QuickLaTeX.com \frac{1}{2}\left[\frac{t^2}{2}\right]_{0}^{\sqrt{3}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d99afdc30e9eb343d69b4d8e93fa666e_l3.png)
![Rendered by QuickLaTeX.com \left[t-\frac{2}{3}t^3+\frac{t^5}{5}\right]_{0}^{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-327e09d5dbc4fcf6e2ef31a9f2c6bbef_l3.png)
![Rendered by QuickLaTeX.com 2a\left[\frac{ttan^2t}{2}-\int \frac{tan^2t}{2}dt\right]_0^\frac{\pi}{4}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c3060df4cbecab428056a535e43cbdd9_l3.png)
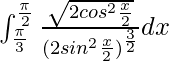
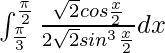
![Rendered by QuickLaTeX.com \left[\frac{t^2}{2}\right]^{\sqrt{3}}_{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fb34ed0542318b4d6b3297735930007c_l3.png)
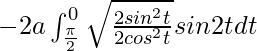
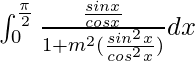
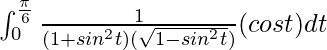
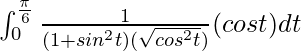
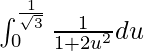
![Rendered by QuickLaTeX.com \frac{1}{\sqrt{2}}\left[tan^{-1}(\sqrt{2}u)\right]_{0}^{\frac{1}{\sqrt{3}}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-20ac359767f60a654802ca43b1e6fb23_l3.png)
![Rendered by QuickLaTeX.com \frac{1}{2}\left[\frac{t^{\frac{4}{3}}}{\frac{4}{3}}\right]_{0}^{8}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7d062a71130f22adcd0a1a7a7c433fa9_l3.png)
![Rendered by QuickLaTeX.com \frac{3}{8}\left[t^{\frac{4}{3}}\right]_{0}^{8}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d1a13d1f97d33c0698e24d58eb033328_l3.png)
![Rendered by QuickLaTeX.com \frac{1}{3}\left[\frac{-1}{u+1}\right]_{0}^{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0ef15c8cdfe4df64fc03a34829f3ffca_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{2t^{\frac{3}{2}}}{3}-\frac{2t^{\frac{7}{2}}}{7}\right]_{0}^{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d5a0f25046aead42022db3e18c87a88f_l3.png)
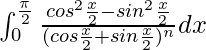
![Rendered by QuickLaTeX.com \left[\frac{2t^{-n+2}}{-n+2}\right]_{1}^{\sqrt{2}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7339548b1f910375dd53748ad7a974d9_l3.png)