Evalúe las siguientes integrales definidas:
Pregunta 1. 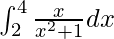
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 2. 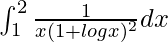
Solución:
Tenemos,
yo =
Sea 1 + log x = t, entonces tenemos,
=> (1/x) dx = 2t dt
Ahora, el límite inferior es, x = 1
=> t = 1 + registro x
=> t = 1 + registro 1
=> t = 1 + 0
=> t = 1
Además, el límite superior es, x = 2
=> t = 1 + registro x
=> t = 1 + registro 2
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 3. 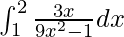
Solución:
Tenemos,
yo =
Sea 9x 2 – 1 = t, entonces tenemos,
=> 18x dx = dt
=> 3x dx = dt/6
Ahora, el límite inferior es, x = 1
=> t = 9x 2 – 1
=> t = 9 (1) 2 – 1
=> t = 9 – 1
=> t = 8
Además, el límite superior es, x = 2
=> t = 9x 2 – 1
=> t = 9 (2) 2 – 1
=> t = 36 – 1
=> t = 35
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 4. 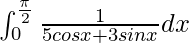
Solución:
Tenemos,
yo =
Al poner sen x =
y cos x =
, obtenemos
yo =
yo =
Sea tan x/2 = t. Entonces tenemos
=>
= dt
Ahora, el límite inferior es, x = 0
=> t = tan x/2
=> t = bronceado 0
=> t = 0
Además, el límite superior es, x = π/2
=> t = tan x/2
=> t = tan π/4
=> t = 1
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 5. 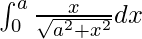
Solución:
Tenemos,
yo =
Sea a 2 + x 2 = t 2 . Entonces tenemos
=> 2x dx = 2t dt
=> x dx = t dt
Ahora, el límite inferior es, x = 0
=> t 2 = un 2 + x 2
=> t 2 = un 2 + 0 2
=> t 2 = un 2
=> t = un
Además, el límite superior es, x = a
=> t 2 = un 2 + x 2
=> t 2 = un 2 + un 2
=> t 2 = 2a 2
=> t = √2 un
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo = √2a – un
yo = un (√2 – 1)
Por lo tanto, el valor de
es a (√2 – 1).
Pregunta 6. 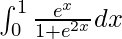
Solución:
Tenemos,
yo =
Sea e x = t. Entonces tenemos
=> e x dx = dt
Ahora, el límite inferior es, x = 0
=> t = e x
=> t = mi 0
=> t = 1
Además, el límite superior es, x = a
=> t = e x
=> t = mi 1
=> t = mi
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 7. 
Solución:
Tenemos,
yo =
Sea x 2 = t. Entonces tenemos
=> 2x dx = dt
Ahora, el límite inferior es, x = 0
= > t = x2
=> t = 0 2
=> t = 0
Además, el límite superior es, x = 1
= > t = x2
=> t = 1 2
=> t = 1
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
pregunta 8 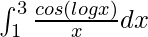
Solución:
Tenemos,
yo =
Sea log x = t. Entonces tenemos
=> (1/x) dx = dt
Ahora, el límite inferior es, x = 1
=> t = log x
=> t = registro 1
=> t = 0
Además, el límite superior es, x = 3
=> t = log x
=> t = registro 3
Entonces, la ecuación se convierte en,
yo =
yo =
I = sen (log 3) – sen 0
I = sen (log 3) – 0
I = pecado (log 3)
Por lo tanto, el valor de
es sen (log 3).
Pregunta 9. 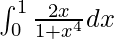
Solución:
Tenemos,
yo =
Sea x 2 = t. Entonces tenemos
=> 2x dx = dt
Ahora, el límite inferior es, x = 0
= > t = x2
=> t = 0 2
=> t = 0
Además, el límite superior es, x = 1
= > t = x2
=> t = 1 2
=> t = 1
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 10. 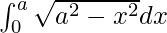
Solución:
Tenemos,
yo =
Sea x = a sen t. Entonces tenemos
=> dx = a cos t dt
Ahora, el límite inferior es, x = 0
=> un pecado t = x
=> un pecado t = 0
=> sen t = 0
=> t = 0
Además, el límite superior es, x = a
=> un pecado t = un
=> un pecado t = un
=> sen t = 1
=> t = π/2
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 11. 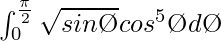
Solución:
Tenemos,
yo =
yo =
Sea sen Ø = t. Entonces tenemos
=> cos Ø dØ = dt
Ahora, el límite inferior es, Ø = 0
=> t = sen Ø
=> t = sen 0
=> t = 0
Además, el límite superior es, Ø = π/2
=> t = sen Ø
=> t = sen π/2
=> t = 1
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 12. 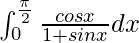
Solución:
Tenemos,
yo =
Sea sen x = t. Entonces tenemos
=> cos x dx = dt
Ahora, el límite inferior es, x = 0
=> t = sen x
=> t = sen 0
=> t = 0
Además, el límite superior es, x = π/2
=> t = sen x
=> t = sen π/2
=> t = 1
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 13. 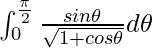
Solución:
Tenemos,
yo =
Sea 1 + cos θ = t 2 . Entonces tenemos
=> – sen θ dθ = 2t dt
=> sen θ dθ = –2t dt
Ahora, el límite inferior es, θ = 0
=> t 2 = 1 + cos θ
=> t 2 = 1 + cos 0
=> t 2 = 1 + 1
=> t 2 = 2
=> t = √2
Además, el límite superior es, θ = π/2
=> t 2 = 1 + cos θ
=> t 2 = 1 + cos π/2
=> t 2 = 1 + 0
=> t 2 = 1
=> t = 1
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 14. 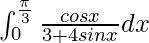
Solución:
Tenemos,
yo =
Sea 3 + 4 sen x = t. Entonces tenemos
=> 0 + 4 cos x dx = dt
=> 4 cos x dx = dt
=> cos x dx = dt/4
Ahora, el límite inferior es, x = 0
=> t = 3 + 4 sen x
=> t = 3 + 4 sen 0
=> t = 3 + 0
=> t = 3
Además, el límite superior es, x = π/3
=> t = 3 + 4 sen x
=> t = 3 + 4 sen π/3
=> t = 3 + 4 (√3/2)
=> t = 3 + 2√3
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 15. 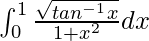
Solución:
Tenemos,
yo =
Sea tan –1 x = t. Entonces tenemos
=> (1/1+x 2 ) dx = dt
Ahora, el límite inferior es, x = 0
=> t = bronceado –1 x
=> t = bronceado –1 0
=> t = 0
Además, el límite superior es, x = 1
=> t = bronceado –1 t
=> t = bronceado –1 1
=> t = π/4
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 16. 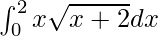
Solución:
Tenemos,
yo =
Sea x + 2 = t 2 . Entonces tenemos
=> dx = 2t dt
Ahora, el límite inferior es, x = 0
=> t 2 = x + 2
=> t 2 = 0 + 2
=> t 2 = 2
=> t = √2
Además, el límite superior es, x = 2
=> t 2 = x + 2
=> t 2 = 2 + 2
=> t 2 = 4
=> t = 2
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 17. 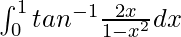
Solución:
Tenemos,
yo =
Sea x = tan t. Entonces tenemos
=> dx = seg 2 t dt
Ahora, el límite inferior es, x = 0
=> bronceado t = x
=> bronceado x = 0
=> x = 0
Además, el límite superior es, x = 1
=> bronceado t = x
=> bronceado x = 1
=> x = π/4
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
Al aplicar el método de integración por partes se obtiene
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 18. 
Solución:
Tenemos,
yo =
Sea sen 2 x = t. Entonces tenemos
=> 2 sen x cos x = dt
=> sen x cos x = dt/2
Ahora, el límite inferior es, x = 0
=> t = sen 2 x
=> t = sen 2 0
=> t = 0
Además, el límite superior es, x = π/2
=> t = sen 2 x
=> t = sen 2 π/2
=> t = 1
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 19. 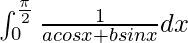
Solución:
Tenemos,
yo =
Al poner cos x =
y sen x =
, obtenemos,
yo =
Sea tan x/2 = t. Entonces tenemos
=> 1/2 seg 2 x/2 dx = dt
=> seg 2 x/2 dx = 2 dt
Ahora, el límite inferior es, x = 0
=> t = tan x/2
=> t = tan 0/2
=> t = bronceado 0
=> t = 0
Además, el límite superior es, x = π/2
=> t = tan x/2
=> t = tan π/4
=> t = 1
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 20. 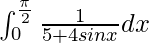
Solución:
Tenemos,
yo =
Al poner sen x =
, obtenemos
yo =
yo =
yo =
yo =
yo =
yo =
Sea tan x/2 = t. Entonces tenemos
=> 1/2 seg 2 x/2 dx = dt
=> seg 2 x/2 dx = 2 dt
Ahora, el límite inferior es, x = 0
=> t = tan x/2
=> t = tan 0/2
=> t = bronceado 0
=> t = 0
Además, el límite superior es, x = π/2
=> t = tan x/2
=> t = tan π/4
=> t = 1
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Publicación traducida automáticamente
Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
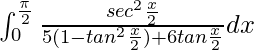
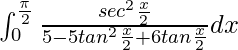
![Rendered by QuickLaTeX.com \left[\frac{2}{5}.\frac{1}{2}\sqrt{\frac{25}{34}}\log\left(\frac{\sqrt{\frac{34}{25}}+t-\frac{3}{5}}{\sqrt{\frac{34}{25}}-t+\frac{3}{5}}\right)\right]^1_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0ffefeca712332617c5ad586720ae9be_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{2}{5}.\frac{1}{2}\frac{5}{\sqrt{34}}\log\left(\frac{\sqrt{\frac{34}{25}}+t-\frac{3}{5}}{\sqrt{\frac{34}{25}}-t+\frac{3}{5}}\right)\right]^1_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-68db90d1bec6cb14c4c722672fa00d36_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{t^{\frac{1}{2}+1}}{\frac{1}{2}+1}+\frac{t^{\frac{9}{2}+1}}{\frac{9}{2}+1}-\frac{2t^{\frac{5}{2}+1}}{\frac{5}{2}+1}\right]_{0}^{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bc93b726dbcf5435fe74436e3bf8e7ad_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{t^{\frac{3}{2}}}{\frac{3}{2}}+\frac{t^{\frac{11}{2}}}{\frac{11}{2}}-\frac{2t^{\frac{7}{2}}}{\frac{7}{2}}\right]_{0}^{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-aa5a36c05af5d28d5f12c8186335778e_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{2t^{\frac{3}{2}}}{3}+\frac{2t^{\frac{11}{2}}}{11}-\frac{4t^{\frac{7}{2}}}{7}\right]_{0}^{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2cb28dbdbb96522d0f11921ed6ae81d8_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{t^{\frac{1}{2}+1}}{\frac{1}{2}+1}\right]_{0}^{\frac{\pi}{4}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f3b01acef7effcd383a4414f6f296c4c_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{t^{\frac{3}{2}}}{\frac{3}{2}}\right]_{0}^{\frac{\pi}{4}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ef5ffffb2183d97f4a21a05ca300312f_l3.png)
![Rendered by QuickLaTeX.com \frac{2}{3}\left[t^{\frac{3}{2}}\right]_{0}^{\frac{\pi}{4}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a51885dae198232d9917f6aebe5dec61_l3.png)
![Rendered by QuickLaTeX.com 2\left[\frac{t^5}{5}-\frac{2t^3}{3}\right]_{\sqrt{2}}^{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bea2a7f4311c727086ab0a3a75ffd837_l3.png)
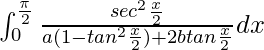
![Rendered by QuickLaTeX.com \frac{2}{a}\int_{0}^{1}\frac{1}{-\left[(t-\frac{b}{a})^2-1-\frac{b^2}{a^2}\right]}dt](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cd1fc88c70f220397d2ba236435d41ac_l3.png)
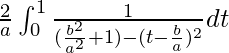
![Rendered by QuickLaTeX.com \left[\frac{2}{a}\left(\frac{1}{2\sqrt{\frac{b^2+a^2}{a^2}}}\right)\log\left(\frac{\sqrt{\frac{b^2+a^2}{a^2}}+(t-\frac{b}{a})}{\sqrt{\frac{b^2+a^2}{a^2}}-(t-\frac{b}{a})}\right)\right]_{0}^{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8a30ace3b32618a0d42bb0fe332d8da6_l3.png)
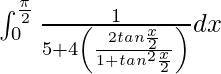
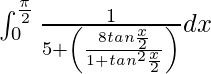

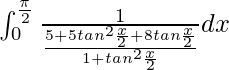
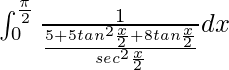
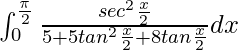
![Rendered by QuickLaTeX.com \frac{2}{3}\left[tan^{-1}(\frac{3-\frac{4}{3}}{1+3(\frac{4}{3})})\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fa1b6716a734ea0c86bd55e23a64fb2b_l3.png)
![Rendered by QuickLaTeX.com \frac{2}{3}\left[tan^{-1}(\frac{\frac{5}{3}}{1+4})\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-072ab951de16d2b16df17ee17c36cc79_l3.png)