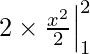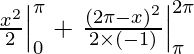Evalúa las siguientes integrales:
Pregunta 15. 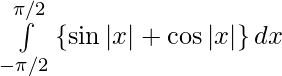
Solución:
Tenemos,
yo =
Como f(- x) = sen|- x| + porque|- x|
= sen |x| + porque |x|
= f(x)
Entonces, f(x) es una función par.
Por lo tanto, obtenemos
yo =
yo =
yo =
yo = 2 (0 + 1 + 1 – 0)
yo = 4
Pregunta 16. 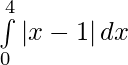
Solución:
Tenemos,
yo =
Sabemos,
Entonces obtenemos,
yo =
yo =
yo =
yo = -1/2 + 1 – 0 + 8 – 4 – 1/2 + 1
yo = 5
Pregunta 17. 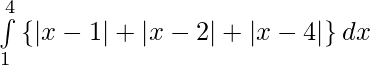
Solución:
Tenemos,
yo =
Sabemos,
Entonces obtenemos,
yo =
yo =
yo = 8 – 4 – 1/2 + 1 – (2 – 4 – 1/2 + 2) + 8 – 8 – 2 + 4 – (8 – 16 – 1/2 + 4)
yo = 23/2
Pregunta 18. 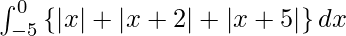
Solución:
Tenemos,
yo =
Sabemos,
Entonces obtenemos,
yo =
yo =
yo = 25/2 – (2 – 4 – 25/2 + 10) – 2 + 4 + (-25/2 + 25)
yo = 63/2
Pregunta 19. 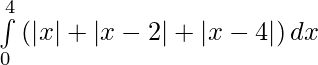
Solución:
Tenemos,
yo =
Sabemos,
Entonces obtenemos,
yo =
yo =
yo = 8 – (2 – 4) + 8 – 8 – 2 + 4 – (8 – 16)
yo = 20
Pregunta 20. 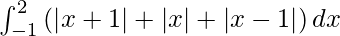
Solución:
Tenemos,
yo =
Sabemos,
Cuando –1 < x < 0,
|x + 1| + |x| + |x – 1| = x + 1 + (- x) + [-(x – 1)]
= 2 – x
Y cuando 0 < x < 1,
|x + 1| + |x| + |x – 1| = x + 1 + x + [-(x – 1)]
= xo + 2
Y cuando 1 ≤ x ≤ 2,
|x + 1| + |x| + |x – 1| = x + 1 + x + x – 1
= 3x
Entonces obtenemos,
yo =
yo =
yo =
yo = – 1/2(4 – 9) + 1/2( 9 – 4) + 3/2(4 – 1)
yo = 5/2 + 5/2 + 9/2
yo = 19/2
Pregunta 21. 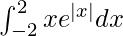
Solución:
Tenemos,
yo =
En ningún lugar,
f(- x) = (- x)e |- x|
= – xe |x|
= – f(x)
Entonces, f(x) es una función impar.
Por lo tanto obtenemos,
yo =
yo = 0
Pregunta 22. 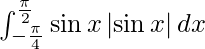
Solución:
Tenemos,
yo =
yo =
Como la conocemos,
yo =
yo =
yo =
yo =
yo =
I = -1/2(0 + π/4) + 1/4(0 + sen π/2) + 1/2 ( π/2 – 0) – 1/4(sen π – 0)
yo = – π/8 + 1/4 (0 + 1) + π/8 – 1/4 (0 – 0)
yo = π/8 + 1/4
Pregunta 23. 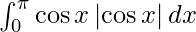
Solución:
Tenemos,
yo =
En ningún lugar,
f(– x) = cos(– x)|cos(– x)|
= -cos x|-cos x|
= – cos x|cos x|
= – f(x)
Entonces, f(x) es una función impar.
Por lo tanto obtenemos,
yo =
yo = 0
Pregunta 24. 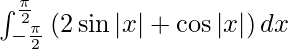
Solución:
Tenemos,
yo =
En ningún lugar,
f(- x) = 2sen|- x| + porque|- x|
= 2sen|x| + porque|x|
= f(x)
Entonces, f(x) es una función impar.
Por lo tanto obtenemos,
yo =
yo =
Como la conocemos,
yo =
yo =
yo =
I = – 4(cos π/2 – cos 0) + 2(sen π/2 – sen 0)
Yo = –4 (0 – 1) + 2 (1 – 0)
yo = 4 + 2
yo = 6
Pregunta 25. 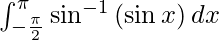
Solución:
Tenemos,
yo =
yo =
yo =
Como π/2 ≤ x ≤ π, obtenemos
=> –π ≤ –x ≤ –π/2
=> 0 ≤ π – x ≤ π/2
Entonces, obtenemos
yo =
yo = 1/2 (π 2/4 – π 2/4 ) – 1/2( 0 – π 2/4 )
yo = 0 + π 2 /8
yo = π 2/8
Pregunta 26. 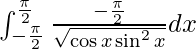
Solución:
Tenemos,
yo =
yo =
yo =
Como la conocemos,
= √cos x|-sen x|
= √cos x|sen x|
= f(x)
Entonces, f(x) es una función impar.
Por lo tanto obtenemos,
yo =
yo =
Como sabemos
,
yo =
yo =
Sea cos x = z 2 . Entonces tenemos
=> – sen x dx = 2z dz
Ahora, el límite inferior es, x = 0
=> z 2 = cos x
=> z 2 = cos 0
=> z 2 = 1
=> z = 1
Además, el límite superior es, x = π/2
=> z 2 = cos x
=> z 2 = cos π/2
=> z 2 = 0
=> z = 0
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
I = – π/2(log1 – log0) + π/2(log1 – log2) + π(tan -1 0 – tan -1 1)
yo = – π/2[0 – ∞] + π/2(0 – log2) + π(0 – π/4)
yo = -∞ – π/2 log2 – π 2 /4
yo = –∞
Pregunta 27. ![Rendered by QuickLaTeX.com \int_0^2 2x\left[ x \right]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8bf48ba5168164ed15afab5c016e7656_l3.png)
Solución:
Tenemos,
yo =
yo =
Como la conocemos,
yo =
yo =
yo =
yo = 4 – 1
yo = 3
Pregunta 28. 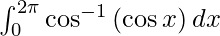
Solución:
Tenemos,
yo =
yo =
Como sabemos, π ≤ x ≤ 2π
=> –2π ≤ –x ≤ –π
=> 0 ≤ 2π – x ≤ π
Por lo tanto, obtenemos
yo =
yo =
yo = 1/2( π – 0) – 1/2(0 – π)
yo = π 2 /2 + π 2 /2
yo = π 2
Publicación traducida automáticamente
Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
![Rendered by QuickLaTeX.com \left[ - \frac{x^2}{2} + x \right]_0^1 + \left[ \frac{x^2}{2} - x \right]_1^4](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-aa416dac73f45a0e162423a1c137c3c6_l3.png)
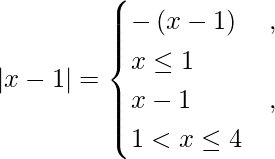
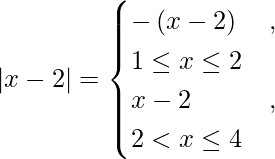
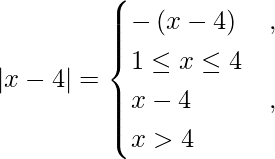
![Rendered by QuickLaTeX.com \left[ \frac{x^2}{2} - x \right]_1^4 - \left[ \frac{x^2}{2} - 2x \right]_1^2 + \left[ \frac{x^2}{2} - 2x \right]_2^4 - \left[ \frac{x^2}{2} - 4x \right]_1^4](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-84fef62a3248152a8d1e2863aa3df05e_l3.png)
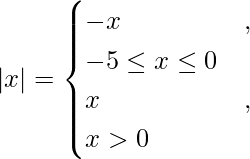
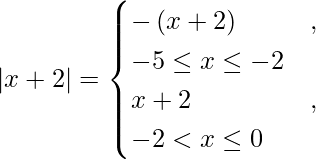
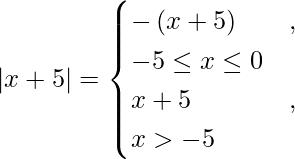
![Rendered by QuickLaTeX.com - \left[ \frac{x^2}{2} \right]_{- 5}^0 - \left[ \frac{x^2}{2} + 2x \right]_{- 5}^{- 2} + \left[ \frac{x^2}{2} + 2x \right]_{- 2}^0 + \left[ \frac{x^2}{2} + 5x \right]_{- 5}^0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6532bd1a446b16d72f54a7090548f172_l3.png)
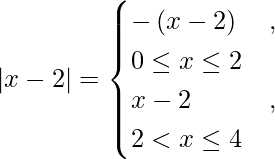
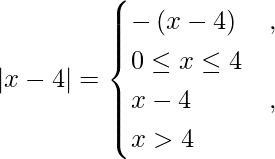
![Rendered by QuickLaTeX.com \left[ \frac{x^2}{2} \right]_0^4 - \left[ \frac{x^2}{2} - 2x \right]_0^2 + \left[ \frac{x^2}{2} - 2x \right]_2^4 - \left[ \frac{x^2}{2} - 4x \right]_0^4](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-01012bb942aa70b5e05b3152ecd42ccc_l3.png)
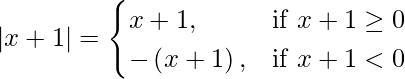
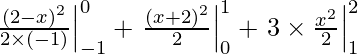
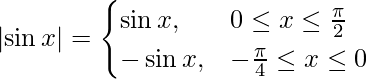
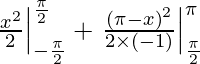
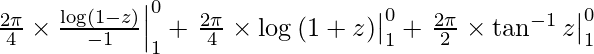
![Rendered by QuickLaTeX.com \left[ x \right] = \begin{cases}0, & 0 \leq x < 1 \\ 1, & 1 \leq x < 2\end{cases}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-714e1693fe24017dd758e61a577d52c1_l3.png)