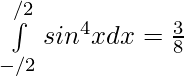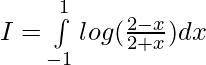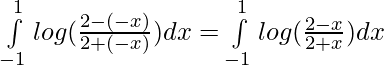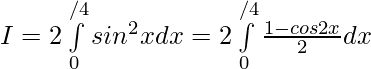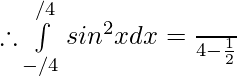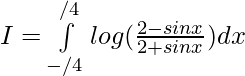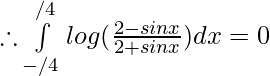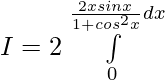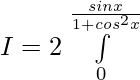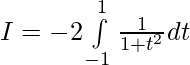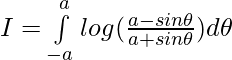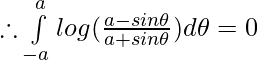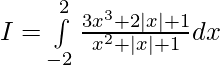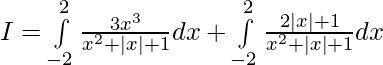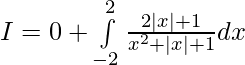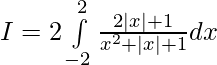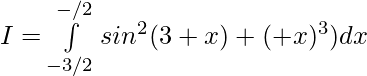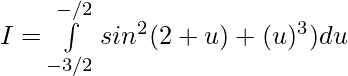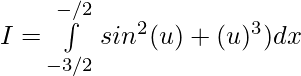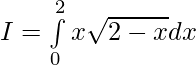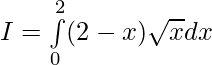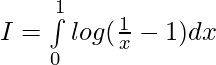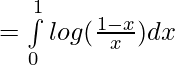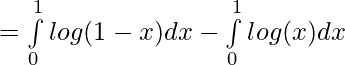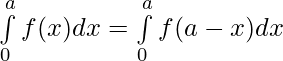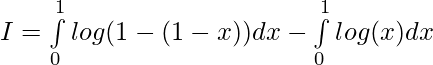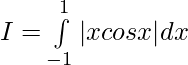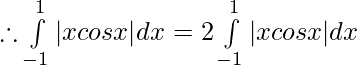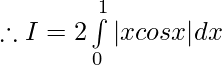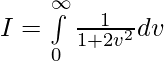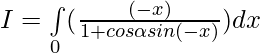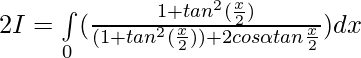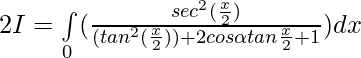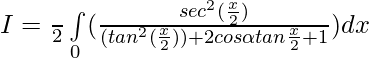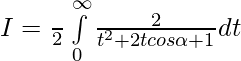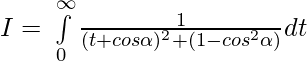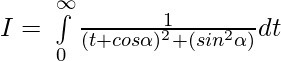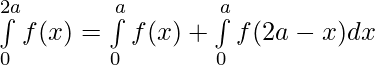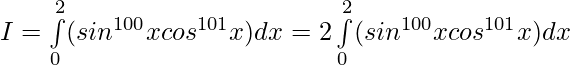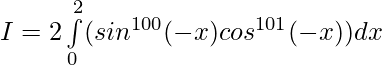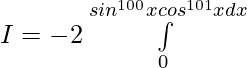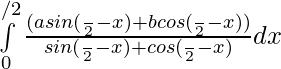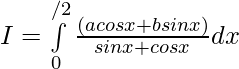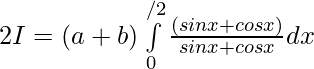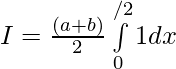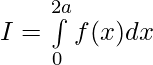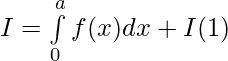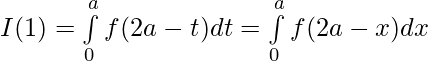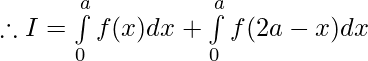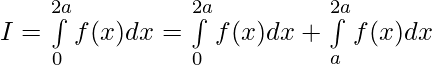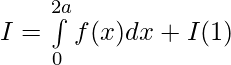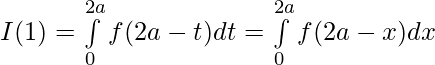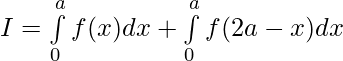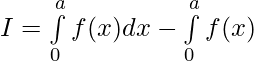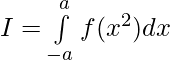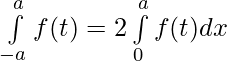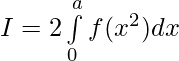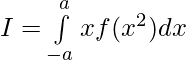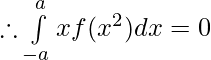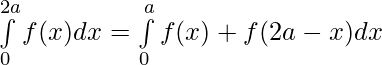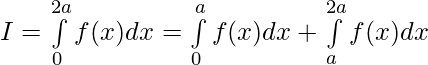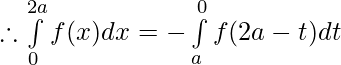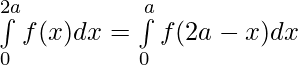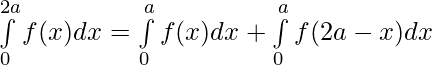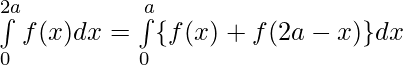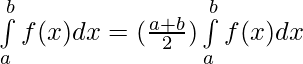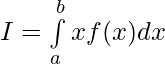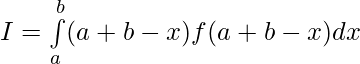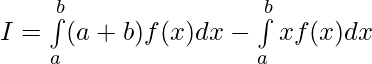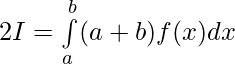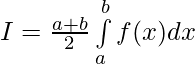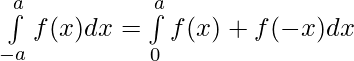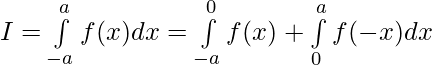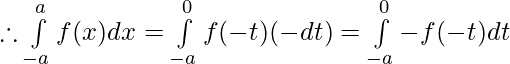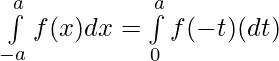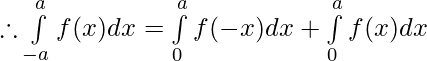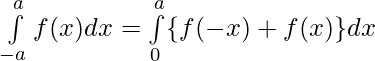Evaluar de cada una de las siguientes integrales (1-46):
Pregunta 1. 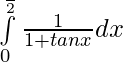
Solución:
Tenemos,
Dejar
—— 1
Entonces,
,
———— 2
Por lo tanto, al sumar 1 y 2 ..
Pregunta 2. 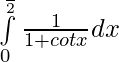 ,
,
Solución:
Tenemos,
Sea, I=
—– 1
Entonces,
—— 2
Sumando 1 y 2 ——-
Pregunta 3. 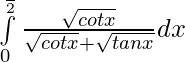 ,
,
Solución:
Tenemos ,
Dejar,
Asi que,
————— 2
Sumando 1 y 2 ——–
Pregunta 4. 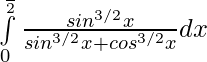
Solución:
Sea,
—— 1
———- 2
Sumando 1 y 2 —–
Pregunta 5. 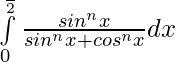
Solución:
Sea,
———– (1)
Asi que,
Pregunta 6. 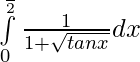
Solución:
———- 1
—– 2
Sumando 1 y 2 ——-
Pregunta 7. 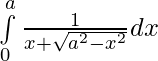
Solución:
Dejar,
dejar
,
Ahora, x=0 ,
, entonces
——————– 1
Asi que,
————- 2
Sumando (1) y (2) —————-
pregunta 8 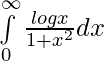
Solución:
Dejar,
después
———— (1)
——————- (2)
Sumar (1) y (2) ————
Pregunta 9. 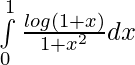
Solución:
Dejar,
Pregunta 10. 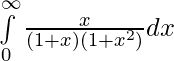
Solución:
Dejar,
Igualando los coeficientes, obtenemos
Asi que,
Pregunta 11. 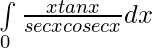
Solución:
————- (1)
—————— (2)
Sumar (1) y (2) —————-
Pregunta 12. 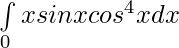
Solución:
Sea ,
————– 1
Asi que,
Dejar,
Como, x=0, t=1; x=π, t=-1
Por eso,
Pregunta 13. 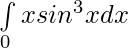
Solución:
Dejar,
Pregunta 14. 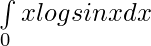
Solución:
tenemos,
=
Como f(x) = f(-x), f(x) es una función par.
————– 1
—————- 2
Sumando 1 y 2 —————-
Ahora deja
Poniendo 2x=t, obtenemos
Pregunta 15. 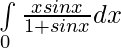
Solución:
Dejar,
Pregunta 16. 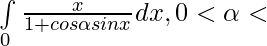
Solución:
Tenemos , I=\int\limits_0^{π} \frac{x}{1+cos\alpha sinx}dx ———- 1
[Tex]=\int\limits_0^{π} \frac{(π-x)}{1+cos\alpha sinx}dx [/Tex]——- 2
Sumando 1 y 2 —-
sustituyendo s
cuando x=0, t=0; x=π,
Pregunta 17. 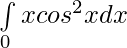
Solución:
Dejar,
Pregunta 18. 
Solución:
Pregunta 19. 
Solución:
Pregunta 20. 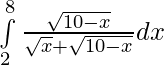
Solución:
Pregunta 21. 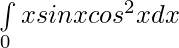
Solución:
Ahora,
Sea cosx=t
senx dx=-dt
[Tex]I= \frac{π }{8}[\fracπ 4+\fracπ 4] dt[/Tex]
Pregunta 22. 
Solución:
—————— 1
———— 2
Sumando 1 y 2 ————-
Dejar ,
Pregunta 23. 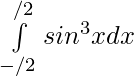
Solución:
Dejar,
Aquí, f(x)=-f(x)
Por lo tanto, f(x) es una función impar
Pregunta 24. 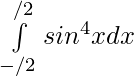
Solución:
Tenemos,
es una función par.
Pregunta 25. 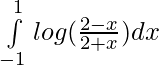
Solución:
tenemos,
Ya que,
esta es una funcion impar
Pregunta 26. 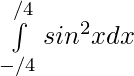
Solución:
tenemos,
sen 2 x es función par
Por eso,
Pregunta 27. 
Solución:
Pregunta 28. 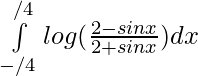
Solución:
tenemos ,
Dejar,
Después,
Pregunta 29. 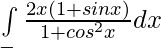
Solución:
Poner cosx = t entonces -senx dx = dt
Pregunta 30. 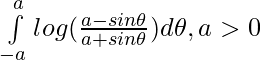
Solución:
Dejar
es una función impar
Pregunta 31. 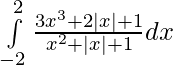
Solución:
Pregunta 32. 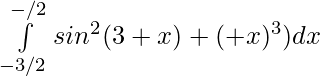
Solución:
Sustituye π+x=u luego dx=du
Pregunta 33. 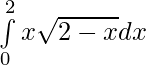
Solución:
Dejar,
Pregunta 34. 
Solución:
Aplicando la propiedad,
De este modo,
–
Pregunta 35. 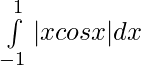
Solución:
Dejar,
Pregunta 36. 
Solución:
[Tex][\porque \int\limits_0^{2a} f(x)dx= 2\int\limits_0^{a} f(x)dx, f(2a-x)=f(x)][/Tex ]
sea tanx = v
dv = seg 2 xdx
Pregunta 37. 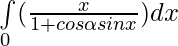
Solución:
Pon
entonces
x=0 ⇒ t=0 y x=π ⇒
Pregunta 38. 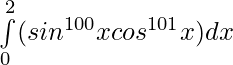
Solución:
sabemos,
También aquí,
f(x) = f(2π -x)
Asi que,
Pregunta 39. 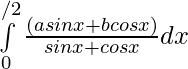
Solución:
después,
Pregunta 40. Si f es una función integrable tal que f(2a-x)=f(x), entonces prueba que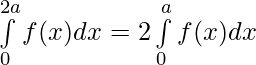
Solución:
Tenemos ,
Después,
Sea , 2a-t =x entonces dx=-dt
si t=a ⇒x=a
si t=2a ⇒ x=0
[Tex]=2\int\limits_{0}^{a}f(x)dx[/Tex]
Por lo tanto Probado.
Pregunta 41. Si 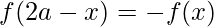 , prueba que
, prueba que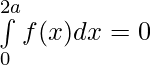
Solución:
Tenemos,
Sea 2a-t=x entonces dx=-dt
t=a, x=a; t=2a, x=0
Pregunta 42. Si f es una función integrable, demuestre que
(i)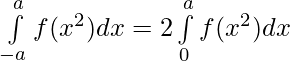
Solución:
tenemos ,
claramente f(x 2 ) es una función par.
Asi que,
(ii)
Solución:
claramente, xf(x 2 ) es una función impar.
Asi que,
Pregunta 43. Si f(x) es una función continua definida en [0,2a] . Entonces, prueba que
Solución:
Tenemos de LHS,
sustituyendo
obtenemos,
Pregunta 44. Si f(a+bx) = f(x), entonces prueba que
Solución:
——————[ Dado que f(a+bx) = f(x) ]
Pregunta 45. Si f(x) es una función continua definida en [-a,a], entonces demuestre que
Solución:
tenemos ,
Sea, x=-t, luego dx=-dt
x=-a ⇒ t=a
x=0 ⇒ t=0
Por lo tanto, Probado.
Pregunta 46. Demuestre que: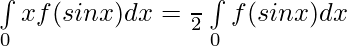
Solución:
Publicación traducida automáticamente
Artículo escrito por ranshu1601 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
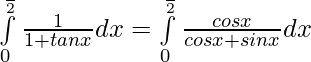
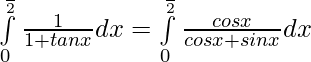
![Rendered by QuickLaTeX.com [\because \int\limits_0^af(x)= \int\limits_0^af(a-x)dx]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4ab50e141d429f5092227dd2e5f9eed1_l3.png)
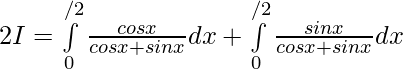
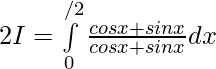
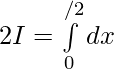



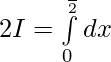
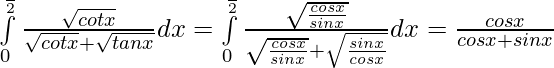

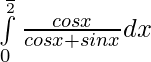
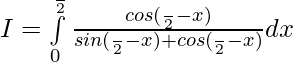
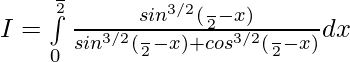
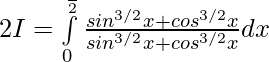
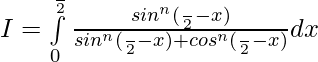
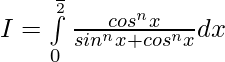
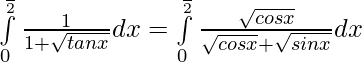

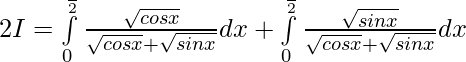
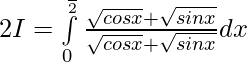

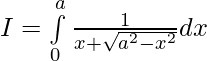

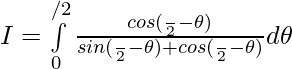
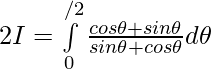
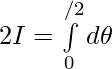
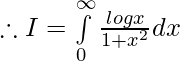
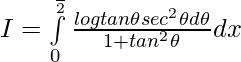
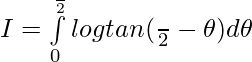
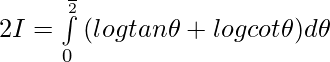
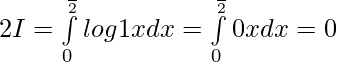
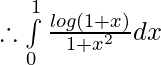
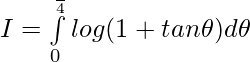
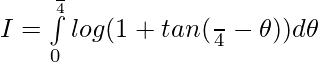
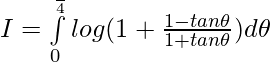
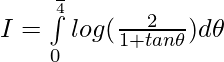
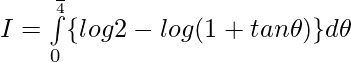
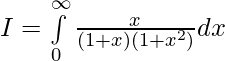
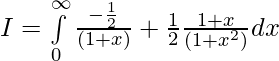
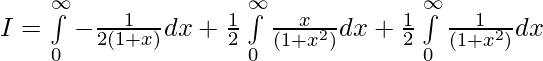
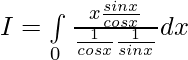
![Rendered by QuickLaTeX.com 2I=\int\limits_0^{π} (π-x)sin^2xdx =π\int\limits_0^{π} \frac{1-cos2x}{2}dx =\frac{π}{2}[π-0-0+0]=\frac{π^2}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d92bda003adaa8eb888a6e831a5254a4_l3.png)
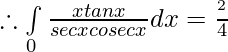
![Rendered by QuickLaTeX.com 2I=π\int\limits_{-1}^{+1}t^4dt = π[\frac{1}{5}+\frac{1}{5}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b415ef8fc36ef74eb5041b09b47938f9_l3.png)
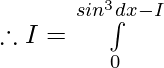



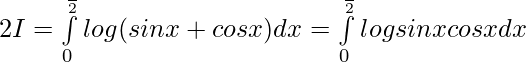
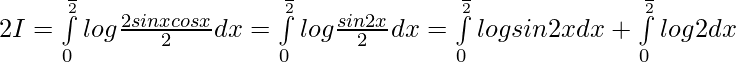
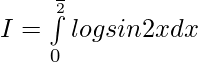
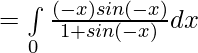
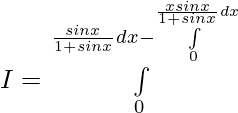
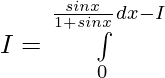
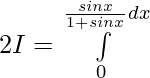
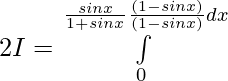
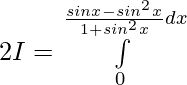
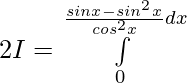
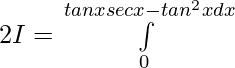
![Rendered by QuickLaTeX.com 2I=π\int\limits_0^π [{tanxsecx}{-(sec^2x-1)}]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-300020cb62bbd109a074ec7c6b53f3a8_l3.png)
![Rendered by QuickLaTeX.com 2I=π\int\limits_0^π [{tanxsecx}{-sec^2x+1)}]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c692e7e93fd63d87b86725ec5f2cf376_l3.png)
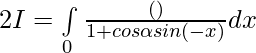




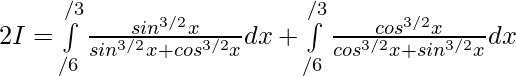

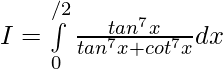
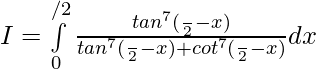
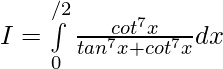

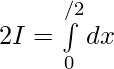
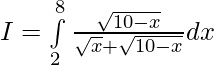
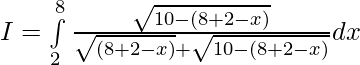
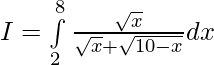




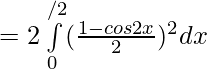
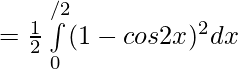
![Rendered by QuickLaTeX.com =\frac12[ \int\limits_{0}^{π/2}( {1+cos^22x}-2cos2x) ]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-96c129032542c89310510bf160f11bd1_l3.png)
![Rendered by QuickLaTeX.com =\frac12[ \int\limits_{0}^{π/2} ( {1-2cos2x}+\frac{1+cos4x}{2}) ]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d5c5041e75f1108d0abcb0e25b575fb1_l3.png)
![Rendered by QuickLaTeX.com =\frac14[ \int\limits_{0}^{π/2}( {3-4cos2x}+cos4x) ]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-058a6a95a41421f55e847b9481aba04c_l3.png)