Clase 12 Soluciones RD Sharma – Capítulo 20 Integrales definidas – Ejercicio 20.5

Evalúe las siguientes integrales definidas como límites de sumas:

Pregunta 23. $\int_{0}^{4}(x+e^{2x})dx$

Solución:

Tenemos,

yo = $\int_{0}^{4}(x+e^{2x})dx$

Sabemos,

$\int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]$ , donde h = $\frac{b-a}{n}$

Aquí a = 0, b = 4 y f(x) = x + e ^2x .

=> h = 4/n

=> nh = 4

Entonces, obtenemos,

yo = $\lim_{h\to0}h[f(0)+f(h)+f(2h)+...+f((n-1)h)]$

= $\lim_{h\to0}h[1+[h+e^{2h}]+[2h+e^{4h}]+...+[(n-1)h+e^{2(n-1)h}]]$

= $\lim_{h\to0}h[h(1+2+3+...+(n-1))+(1+e^{2h}+e^{4h}+...e^{2(n-1)h})]$

= $\lim_{h\to0}h[h(\frac{n(n-1)}{2})+(\frac{(e^{2h})^2-1}{e^{2h}-1})]$

= $\lim_{h\to0}h[h(\frac{n(n-1)}{2})+(\frac{e^{2nh}-1}{e^{2h}-1})]$

= $\lim_{h\to0}h^2\left[(\frac{n(n-1)}{2})+\left(\frac{e^{8}-1}{2(\frac{e^{2h}-1}{h})}\right)\right]$

Ahora bien, si h −> 0, entonces n −> ∞. Entonces tenemos,

= $\lim_{n\to\infty}[\frac{16}{n^2}(\frac{n(n-1)}{2})+(\frac{e^{8}-1}{2})]$

= $\lim_{n\to\infty}[\frac{8n^2}{n^2}(1-\frac{1}{n})+(\frac{e^{8}-1}{2})]$

= $8+(\frac{e^{8}-1}{2})$

= $\frac{15+e^{8}}{2}$

Por lo tanto, el valor de $\int_{0}^{4}(x+e^{2x})dx$ como límite de la suma es $\frac{15+e^{8}}{2}$ .

Pregunta 24. 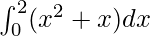$\int_{0}^{2}(x^2+x)dx$

Solución:

Tenemos,

yo = $\int_{0}^{2}(x^2+x)dx$

Sabemos,

$\int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]$ , donde h = $\frac{b-a}{n}$

Aquí a = 0, b = 2 y f(x) = x ² + x.

=> h = 2/n

=> nh = 2

Entonces, obtenemos,

yo = $\lim_{h\to0}h[f(0)+f(h)+f(2h)+...+f((n-1)h)]$

= $\lim_{h\to0}h[0+(h^2+h)+[(2h)^2+2h]+...+[(n-1)h)^2+(n-1)h]]$

= $\lim_{h\to0}h[h^2(1^2+2^2+3^2+...(n-1)^2)+h(1+2+3+...+(n-1))]$

= $\lim_{h\to0}h[h^2(\frac{n(n-1)(2n-1)}{6})+h(\frac{n(n-1)}{2})]$

Ahora bien, si h −> 0, entonces n −> ∞. Entonces tenemos,

= $\lim_{n\to\infty}\frac{2}{n}[\frac{4}{n^2}(\frac{n(n-1)(2n-1)}{6})+\frac{2}{n}(\frac{n(n-1)}{2})]$

= $\lim_{n\to\infty}[\frac{4n^3}{n^3}(1-\frac{1}{n})(2-\frac{1}{n})+\frac{2n^2}{n^2}(1-\frac{1}{n})]$

= $\frac{8}{3}+2$

= $\frac{14}{3}$

Por lo tanto, el valor de $\int_{0}^{2}(x^2+x)dx$ como límite de la suma es $\frac{14}{3}$ .

Pregunta 25. 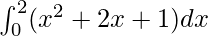$\int_{0}^{2}(x^2+2x+1)dx$

Solución:

Tenemos,

yo = $\int_{0}^{2}(x^2+2x+1)dx$

Sabemos,

$\int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]$ , donde h = $\frac{b-a}{n}$

Aquí a = 0, b = 2 y f(x) = x ² + 2x + 1.

=> h = 2/n

=> nh = 2

Entonces, obtenemos,

yo = $\lim_{h\to0}h[f(0)+f(h)+f(2h)+...+f((n-1)h)]$

= $\lim_{h\to0}h[1+(h^2+2h+1)+[(2h)^2+2(2h)+1]+...[(n-1)^2+2(n-1)+1]$

= $\lim_{h\to0}h[n+h^2(1^2+2^2+3^2+...(n-1)^2)+2h(1+2+3+...+(n-1))]$

= $\lim_{h\to0}h[n+h^2(\frac{n(n-1)(2n-1)}{6})+2h(\frac{n(n-1)}{2})]$

Ahora bien, si h −> 0, entonces n −> ∞. Entonces tenemos,

= $\lim_{n\to\infty}\frac{2}{n}[n+\frac{4}{n^2}(\frac{n(n-1)(2n-1)}{6})+\frac{4}{n}(\frac{n(n-1)}{2})]$

= $\lim_{n\to\infty}[2+\frac{4n^3}{n^3}(1-\frac{1}{n})(2-\frac{1}{n})+\frac{4n^2}{n^2}(1-\frac{1}{n})]$

= $2+\frac{8}{3}+4$

= $\frac{26}{3}$

Por lo tanto, el valor de $\int_{0}^{2}(x^2+2x+1)dx$ como límite de la suma es $\frac{26}{3}$ .

Pregunta 26. 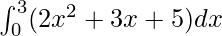$\int_{0}^{3}(2x^2+3x+5)dx$

Solución:

Tenemos,

yo = $\int_{0}^{3}(2x^2+3x+5)dx$

Sabemos,

$\int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]$ , donde h = $\frac{b-a}{n}$

Aquí a = 0, b = 3 y f(x) = 2x ² + 3x + 5.

=> h = 3/n

=> nh = 3

Entonces, obtenemos,

yo = $\lim_{h\to0}h[f(0)+f(h)+f(2h)+...+f((n-1)h)]$

= $\lim_{h\to0}h[5+(2h^2+3h+5)+[2(2h)^2+3(2h)+5]+...+[2(n-1)^2h^2+3((n-1)h)+5]]$

= $\lim_{h\to0}h[5n+2h^2(1^2+2^2+3^2+...+(n-1)^2)+3h(1+2+3+...+(n-1))]$

= $\lim_{h\to0}h[5n+2h^2(\frac{n(n-1)(2n-1)}{6})+3h(\frac{n(n-1)}{2})]$

Ahora bien, si h −> 0, entonces n −> ∞. Entonces tenemos,

= $\lim_{n\to\infty}\frac{3}{n}[5n+\frac{18}{n^2}(\frac{n(n-1)(2n-1)}{6})+\frac{9}{n}(\frac{n(n-1)}{2})]$

= $\lim_{n\to\infty}[15+\frac{9n^3}{n^3}(1-\frac{1}{n})(2-\frac{1}{n})+\frac{27n^2}{2n^2}(1-\frac{1}{n})]$

= 15 + 18 + $\frac{27}{2}$

= $\frac{93}{2}$

Por lo tanto, el valor de $\int_{0}^{3}(2x^2+3x+5)dx$ como límite de la suma es $\frac{93}{2}$ .

Pregunta 27. 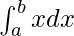$\int_{a}^{b}xdx$

Solución:

Tenemos,

yo = $\int_{a}^{b}xdx$

Sabemos,

$\int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]$ , donde h = $\frac{b-a}{n}$

Aquí a = a, b = b y f(x) = x.

=> h = $\frac{b-a}{n}$

=> nh = segundo − un

Entonces, obtenemos,

yo = $\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]$

= $\lim_{h\to0}h[a+(a+h)+(a+2h)+...+(a+(n-1)h)]$

= $\lim_{h\to0}h[na+h(1+2+3+...+(n-1))]$

= $\lim_{h\to0}h[na+h(\frac{n(n-1)}{2})]$

Ahora bien, si h −> 0, entonces n −> ∞. Entonces tenemos,

= $\lim_{n\to\infty}\frac{b-a}{n}[na+\frac{b-a}{n}(\frac{n(n-1)}{2})]$

= $\lim_{n\to\infty}(b-a)[a+\frac{b-a}{n}(\frac{n-1}{2})]$

= $\lim_{n\to\infty}(b-a)[a+(b-a)(\frac{1-\frac{1}{n}}{2})]$

= $(b-a)[a+\frac{b-a}{2}]$

= $\frac{(b-a)(b+a)}{2}$

= $\frac{b^2-a^2}{2}$

Por lo tanto, el valor de $\int_{a}^{b}xdx$ como límite de la suma es $\frac{b^2-a^2}{2}$ .

Pregunta 28. 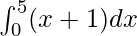$\int_{0}^{5}(x+1)dx$

Solución:

Tenemos,

yo = $\int_{0}^{5}(x+1)dx$

Sabemos,

$\int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]$ , donde h = $\frac{b-a}{n}$

Aquí a = 0, b = 5 y f(x) = x + 1.

=> h =5/n

=> nh = 5

Entonces, obtenemos,

yo = $\lim_{h\to0}h[f(0)+f(h)+f(2h)+...+f((n-1)h)]$

= $\lim_{h\to0}h[1+(h+1)+(2h+1)+...+((n-1)h+1)]$

= $\lim_{h\to0}h[n+h(1+2+3+...+(n-1))]$

= $\lim_{h\to0}h[n+h(\frac{n(n-1)}{2})]$

Ahora bien, si h −> 0, entonces n −> ∞. Entonces tenemos,

= $\lim_{n\to\infty}\frac{5}{n}[n+\frac{5}{n}(\frac{n(n-1)}{2})]$

= $\lim_{n\to\infty}[5+\frac{25n^2}{2n^2}(1-\frac{1}{n})]$

= 5 + $\frac{25}{2}$

= $\frac{35}{2}$

Por lo tanto, el valor de $\int_{0}^{5}(x+1)dx$ como límite de la suma es $\frac{35}{2}$ .

Pregunta 29. 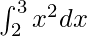$\int_{2}^{3}x^2dx$

Solución:

Tenemos,

yo = $\int_{2}^{3}x^2dx$

Sabemos,

$\int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]$ , donde h = $\frac{b-a}{n}$

Aquí a = 2, b = 3 y f(x) = x ² .

=> h = 1/n

=> nh = 1

Entonces, obtenemos,

yo = $\lim_{h\to0}h[f(2)+f(2+h)+f(2+2h)+...+f(2+(n-1)h)]$

= $\lim_{h\to0}h[4+(2+h)^2+(2+2h)^2+...+(2+(n-1)h)^2]$

= $\lim_{h\to0}h[4+[2^2+2.h+h^2]+[2^2+2.2h+(2h)^2]+...]$

= $\lim_{h\to0}h[4n+h^2(1^2+2^2+...+(n-1)^2)+4h(1+2+3+...+(n-1))]$

= $\lim_{h\to0}h[4n+h^2(\frac{n(n-1)(2n-1)}{6})+4h(\frac{n(n-1)}{2})]$

Ahora bien, si h −> 0, entonces n −> ∞. Entonces tenemos,

= $\lim_{n\to\infty}\frac{1}{n}[4n+\frac{1}{n^2}(\frac{n(n-1)(2n-1)}{6})+\frac{4}{n}(\frac{n(n-1)}{2})]$

= $\lim_{n\to\infty}[4+\frac{n^3}{6n^3}(1-\frac{1}{n})(2-\frac{1}{n})+\frac{2n^2}{n^2}(1-\frac{1}{n})]$

= $4+\frac{2}{6}+2$

= $4+\frac{1}{3}+2$

= $\frac{19}{3}$

Por lo tanto, el valor de $\int_{2}^{3}x^2dx$ como límite de la suma es $\frac{19}{3}$ .

Pregunta 30. 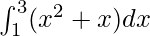$\int_{1}^{3}(x^2+x)dx$

Solución:

Tenemos,

yo = $\int_{1}^{3}(x^2+x)dx$

Sabemos,

$\int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]$ , donde h = $\frac{b-a}{n}$

Aquí a = 1, b = 3 y f(x) = x ² + x.

=> h = 2/n

=> nh = 2

Entonces, obtenemos,

yo = $\lim_{h\to0}h[f(1)+f(1+h)+f(1+2h)+...+f(1+(n-1)h)]$

= $\lim_{h\to0}h[2+[(1+h)^2+(1+h)]+[(1+2h)^2+(1+2h)]+...]$

= $\lim_{h\to0}h[2n+h^2(1^2+2^2+3^2+...+(n-1)^2)+3h(1+2+3+...+(n-1))]$

= $\lim_{h\to0}h[2n+h^2(\frac{n(n-1)(2n-1)}{6})+3h(\frac{n(n-1)}{2})]$

Ahora bien, si h −> 0, entonces n −> ∞. Entonces tenemos,

= $\lim_{n\to\infty}\frac{2}{n}[2n+\frac{4}{n^2}(\frac{n(n-1)(2n-1)}{6})+\frac{6}{n}(\frac{n(n-1)}{2})]$

= $\lim_{n\to\infty}[4+\frac{4n^3}{3n^3}(1-\frac{1}{n})(2-\frac{1}{n})+\frac{6n^2}{n^2}(1-\frac{1}{n})]$

= $4+\frac{8}{3}+6$

= $\frac{38}{3}$

Por lo tanto, el valor de $\int_{1}^{3}(x^2+x)dx$ como límite de la suma es $\frac{38}{3}$ .

Pregunta 31. 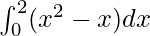$\int_{0}^{2}(x^2-x)dx$

Solución:

Tenemos,

yo = $\int_{0}^{2}(x^2-x)dx$

Sabemos,

$\int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]$ , donde h = $\frac{b-a}{n}$

Aquí a = 0, b = 2 y f(x) = x ² − x.

=> h = 2/n

=> nh = 2

Entonces, obtenemos,

yo = $\lim_{h\to0}h[f(0)+f(h)+f(2h)+...+f((n-1)h)]$

= $\lim_{h\to0}h[0+[h^2-h]+[(2h)^2-2h]+...]$

= $\lim_{h\to0}h[h^2(1^2+2^2+...+(n-1)^2)-h(1+2+...+(n-1))]$

= $\lim_{h\to0}h[h^2(\frac{n(n-1)(2n-1)}{6})-h(\frac{n(n-1)}{2})]$

Ahora bien, si h −> 0, entonces n −> ∞. Entonces tenemos,

= $\lim_{n\to\infty}\frac{2}{n}[\frac{4}{n^2}(\frac{n(n-1)(2n-1)}{6})-\frac{2}{n}(\frac{n(n-1)}{2})]$

= $\lim_{n\to\infty}[\frac{4n^3}{3n^3}(1-\frac{1}{n})(2-\frac{1}{n})-\frac{2n^2}{n^2}(1-\frac{1}{n})]$

= $\frac{8}{3}-2$

= $\frac{2}{3}$

Por lo tanto, el valor de $\int_{0}^{2}(x^2-x)dx$ como límite de la suma es $\frac{2}{3}$ .

Pregunta 32. 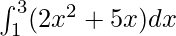$\int_{1}^{3}(2x^2+5x)dx$

Solución:

Tenemos,

yo = $\int_{1}^{3}(2x^2+5x)dx$

Sabemos,

$\int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]$ , donde h = $\frac{b-a}{n}$

Aquí a = 1, b = 3 y f(x) = 2x ² + 5x.

=> h = 2/n

=> nh = 2

Entonces, obtenemos,

yo = $\lim_{h\to0}h[f(1)+f(1+h)+f(1+2h)+...+f(1+(n-1)h)]$

= $\lim_{h\to0}h[7+[2(1+h)^2+5(1+h)]+[2(1+2h)^2+5(1+2h)]+...]$

= $\lim_{h\to0}h[7n+9h(1+2+3+...+(n-1))+2h^2(1^2+2^2+3^2+...(n-1)^2)]$

= $\lim_{h\to0}h[7n+9h(\frac{n(n+1)}{2})+2h^2(\frac{n(n-1)(2n-1)}{6})]$

Ahora bien, si h −> 0, entonces n −> ∞. Entonces tenemos,

= $\lim_{n\to\infty}\frac{2}{n}[7n+\frac{18}{n}(\frac{n(n-1)}{2})+\frac{8}{n^2}(\frac{n(n-1)(2n-1)}{6})]$

= $\lim_{n\to\infty}[14+\frac{18n^2}{n^2}(1-\frac{1}{n})+\frac{8n^3}{3n^3}(1-\frac{1}{n})(2-\frac{1}{n})]$

= 14 + 18 + $\frac{16}{3}$

= $\frac{112}{3}$

Por lo tanto, el valor de $\int_{1}^{3}(2x^2+5x)dx$ como límite de la suma es $\frac{112}{3}$ .

Pregunta 33. 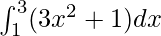$\int_{1}^{3}(3x^2+1)dx$

Solución:

Tenemos,

yo = $\int_{1}^{3}(3x^2+1)dx$

Sabemos,

$\int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]$ , donde h = $\frac{b-a}{n}$

Aquí a = 1, b = 3 y f(x) = 3x ² + 1.

=> h = 2/n

=> nh = 2

Entonces, obtenemos,

yo = $\lim_{h\to0}h[f(1)+f(1+h)+f(1+2h)+...+f(1+(n-1)h)]$

= $\lim_{h\to0}h[4+[3(1+h)^2+1]+[3(1+2h)^2+1]+...]$

= $\lim_{h\to0}h[4n+6h(1+2+3+...(n-1))+3h^2(1^2+2^2+3^2+...(n-1)^2)]$

= $\lim_{h\to0}h[4n+6h(\frac{n(n-1)}{2})+3h^2(\frac{n(n-1)(2n-1)}{6})]$

Ahora bien, si h −> 0, entonces n −> ∞. Entonces tenemos,

= $\lim_{n\to\infty}\frac{2}{n}[4n+\frac{12}{n}(\frac{n(n-1)}{2})+\frac{12}{n^2}(\frac{n(n-1)(2n-1)}{6})]$

= $\lim_{n\to\infty}[8+\frac{12n^2}{n^2}(1-\frac{1}{n})+\frac{4n^3}{n^3}(1-\frac{1}{n})(2-\frac{1}{n})]$

= 8 + 12 + 8

= 28

Por lo tanto, el valor de $\int_{1}^{3}(3x^2+1)dx$ como límite de la suma es 28.