Clase 12 Soluciones RD Sharma – Capítulo 20 Integrales definidas – Ejercicio 20.5

Evalúe las siguientes integrales definidas como límites de sumas:

Pregunta 1. 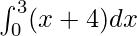$\int_{0}^{3}(x+4)dx$

Solución:

Tenemos,

yo = $\int_{0}^{3}(x+4)dx$

Sabemos, $\int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]$ , donde h = $\frac{b-a}{n}$

Aquí a = 0, b = 3 y f(x) = x + 4.

=> h = 3/n

=> nh = 3

Entonces, obtenemos,

yo = $\lim_{h\to0}h[f(0)+f(h)+f(2h)+...+f((n-1)h)]$

= $\lim_{h\to0}h[4+(h+4)+(2h+4)+...+(n-1)h+4]$

= $\lim_{h\to0}h[4n+h(1+2+3+...+(n-1))]$

= $\lim_{h\to0}h[4n+h(\frac{n(n-1)}{2})]$

Ahora bien, si h −> 0, entonces n −> ∞. Entonces tenemos,

= $\lim_{n\to\infty}\frac{3}{n}[4n+\frac{3}{n}(\frac{n(n-1)}{2})]$

= $\lim_{n\to\infty}\left[12+\frac{9}{2}(1-\frac{1}{n})\right]$

= 12 + $\frac{9}{2}$

= $\frac{33}{2}$

Por lo tanto, el valor de $\int_{0}^{3}(x+4)dx$ como límite de la suma es $\frac{33}{2}$ .

Pregunta 2. 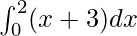$\int_{0}^{2}(x+3)dx$

Solución:

Tenemos,

yo = $\int_{0}^{2}(x+3)dx$

Sabemos,

$\int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]$ , donde h = $\frac{b-a}{n}$

Aquí a = 0, b = 2 y f(x) = x + 3.

=> h = 2/n

=> nh = 2

Entonces, obtenemos,

yo = $\lim_{h\to0}h[f(0)+f(h)+f(2h)+...+f((n-1)h)]$

= $\lim_{h\to0}h[3+(h+3)+(2h+3)+...+(n-1)h+3]$

= $\lim_{h\to0}h[3n+h(1+2+3+...+(n-1))]$

= $\lim_{h\to0}h[3n+h(\frac{n(n-1)}{2})]$

Ahora bien, si h −> 0, entonces n −> ∞. Entonces tenemos,

= $\lim_{n\to\infty}\frac{2}{n}[3n+\frac{2}{n}(\frac{n(n-1)}{2})]$

= $\lim_{n\to\infty}[6+2(1-\frac{1}{n})]$

= 6 + 2

= 8

Por lo tanto, el valor de $\int_{0}^{2}(x+3)dx$ como límite de la suma es 8.

Pregunta 3. 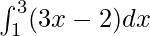$\int_{1}^{3}(3x-2)dx$

Solución:

Tenemos,

yo = $\int_{1}^{3}(3x-2)dx$

Sabemos,

$\int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]$ , donde h = $\frac{b-a}{n}$

Aquí a = 1, b = 3 y f(x) = 3x − 2.

=> h = 2/n

=> nh = 2

Entonces, obtenemos,

yo = $\lim_{h\to0}h[f(1)+f(1+h)+f(1+2h)+...+f(1+(n-1)h)]$

= $\lim_{h\to0}h[1+[3(1+h)-2]+[3(1+2h)-2]+...+[3(1+(n-1)h)-2]]$

= $\lim_{h\to0}h[n+3h(1+2+3+...+(n-1))]$

= $\lim_{h\to0}h[n+3h(\frac{n(n-1)}{2})]$

Ahora bien, si h −> 0, entonces n −> ∞. Entonces tenemos,

= $\lim_{n\to\infty}\frac{2}{n}[n+\frac{6}{n}(\frac{n(n-1)}{2})]$

= $\lim_{n\to\infty}[2+6(1-\frac{1}{n})]$

= 2 + 6

= 8

Por lo tanto, el valor de $\int_{1}^{3}(3x-2)dx$ como límite de la suma es 8.

Pregunta 4. 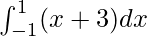$\int_{-1}^{1}(x+3)dx$

Solución:

Tenemos,

yo = $\int_{-1}^{1}(x+3)dx$

Sabemos,

$\int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]$ , donde h = $\frac{b-a}{n}$

Aquí a = −1, b = 1 y f(x) = x + 3.

=> h = 2/n

=> nh = 2

Entonces, obtenemos,

yo = $\lim_{h\to0}h[f(-1)+f(-1+h)+f(-1+2h)+...+f(-1+(n-1)h)]$

= $\lim_{h\to0}h[2+(2+h)+(2+2h)+...+((n-1)h+2)]$

= $\lim_{h\to0}h[2n+h(1+2+3+...+(n-1))]$

= $\lim_{h\to0}h[2n+h(\frac{n(n-1)}{2})]$

Ahora bien, si h −> 0, entonces n −> ∞. Entonces tenemos,

= $\lim_{n\to\infty}\frac{2}{n}[2n+\frac{2}{n}(\frac{n(n-1)}{2})]$

= $\lim_{n\to\infty}[4+2(1-\frac{1}{n})]$

= 4 + 2

= 6

Por lo tanto, el valor de $\int_{-1}^{1}(x+3)dx$ como límite de la suma es 6.

Pregunta 5. 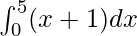$\int_{0}^{5}(x+1)dx$

Solución:

Tenemos,

yo = $\int_{0}^{5}(x+1)dx$

Sabemos,

$\int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]$ , donde h = $\frac{b-a}{n}$

Aquí a = 0, b = 5 y f(x) = x + 1.

=> h = 5/n

=> nh = 5

Entonces, obtenemos,

yo = $\lim_{h\to0}h[f(0)+f(h)+f(2h)+...+f((n-1)h)]$

= $\lim_{h\to0}h[1+(h+1)+(2h+1)+...+((n-1)h+1)]$

= $\lim_{h\to0}h[n+h(1+2+3+...+(n-1))]$

= $\lim_{h\to0}h[n+h(\frac{n(n-1)}{2})]$

Ahora bien, si h −> 0, entonces n −> ∞. Entonces tenemos,

= $\lim_{n\to\infty}\frac{5}{n}[n+\frac{5}{n}(\frac{n(n-1)}{2})]$

= $\lim_{n\to\infty}[5+\frac{25}{2}(1-\frac{1}{n})]$

= 5 + $\frac{25}{2}$

= $\frac{35}{2}$

Por lo tanto, el valor de $\int_{0}^{5}(x+1)dx$ como límite de la suma es $\frac{35}{2}$ .

Pregunta 6. 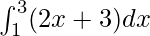$\int_{1}^{3}(2x+3)dx$

Solución:

Tenemos,

yo = $\int_{1}^{3}(2x+3)dx$

Sabemos,

$\int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]$ , dónde $h = \frac{b-a}{n}$

Aquí a = 1, b = 3 y f(x) = 2x + 3.

=> h = 2/n

=> nh = 2

Entonces, obtenemos,

yo = $\lim_{h\to0}h[f(1)+f(1+h)+f(1+2h)+...+f(1+(n-1)h)]$

= $\lim_{h\to0}h[2+3+[2(1+h)+3]+[2(1+2h)+3]+...+[2(1+(n-1)h+3)]]$

= $\lim_{h\to0}h[5+(5+2h)+(5+4h)+...+(5+2(n-1)h)]$

= $\lim_{h\to0}h[5n+2h(1+2+3+...+(n-1))]$

= $\lim_{h\to0}h[5n+2h(\frac{n(n-1)}{2})]$

Ahora bien, si h −> 0, entonces n −> ∞. Entonces tenemos,

= $\lim_{n\to\infty}\frac{2}{n}[5n+\frac{4}{n}(\frac{n(n-1)}{2})]$

= $\lim_{n\to\infty}[10+4(1-\frac{1}{n})]$

= 10 + 4

= 14

Por lo tanto, el valor de $\int_{1}^{3}(2x+3)dx$ como límite de la suma es 14.

Pregunta 7. 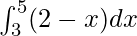$\int_{3}^{5}(2-x)dx$

Solución:

Tenemos,

yo = $\int_{3}^{5}(2-x)dx$

Sabemos,

$\int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]$ , donde h = $\frac{b-a}{n}$

Aquí a = 3, b = 5 y f(x) = 2 − x.

=> h = 2/n

=> nh = 2

Entonces, obtenemos,

yo = $\lim_{h\to0}h[f(3)+f(3+h)+f(3+2h)+...+f(3+(n-1)h)]$

= $\lim_{h\to0}h[(2-3)+(2-(3+h))+f(2-(3+2h))+...+f(2-(3+(n-1)h))]$

= $\lim_{h\to0}h[-1+(-1-h)+(-1-2h)+...+(-1-(n-1)h)]$

= $\lim_{h\to0}h[-n-h(1+2+3+...+(n-1))]$

= $\lim_{h\to0}h[-n-h(\frac{n(n-1)}{2})]$

Ahora bien, si h −> 0, entonces n −> ∞. Entonces tenemos,

= $\lim_{n\to\infty}\frac{2}{n}[-n-\frac{2}{n}(\frac{n(n-1)}{2})]$

= $\lim_{n\to\infty}[-2-2(1-\frac{1}{n})]$

= –2 – 2

= –4

Por tanto, el valor de $\int_{3}^{5}(2-x)dx$ como límite de la suma es –4.

pregunta 8 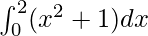$\int_{0}^{2}(x^2+1)dx$

Solución:

Tenemos,

yo = $\int_{0}^{2}(x^2+1)dx$

Sabemos,

$\int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]$ , donde h = $\frac{b-a}{n}$

Aquí a = 0, b = 2 y f(x) = x ² + 1.

=> h = 2/n

=> nh = 2

Entonces, obtenemos,

yo = $\lim_{h\to0}h[f(0)+f(h)+f(2h)+...+f((n-1)h)]$

= $\lim_{h\to0}h[1+(h^2+1)+((2h)^2+1)+...+(((n-1)h)^2+1)]$

= $\lim_{h\to0}h[n+h^2(1^2+2^2+3^2+...+(n-1)^2)]$

= $\lim_{h\to0}h[n+h^2\frac{n(n-1)(2n-1)}{6}]$

Ahora bien, si h −> 0, entonces n −> ∞. Entonces tenemos,

= $\lim_{n\to\infty}\frac{2}{n}[n+\frac{4}{n^2}\frac{n(n-1)(2n-1)}{6}]$

= $\lim_{n\to\infty}[2+\frac{4n^3}{3n^3}(1-\frac{1}{n})(2-\frac{1}{n})]$

= $2+\frac{4×2}{3}$

= $2+\frac{8}{3}$

= $\frac{14}{3}$

Por lo tanto, el valor de $\int_{0}^{2}(x^2+1)dx$ como límite de la suma es $\frac{14}{3}$ .

Pregunta 9. 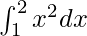$\int_{1}^{2}x^2dx$

Solución:

Tenemos,

yo = $\int_{1}^{2}x^2dx$

Sabemos,

$\int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]$ , donde h = $\frac{b-a}{n}$

Aquí a = 1, b = 2 y f(x) = x2.

=> h = 1/n

=> nh = 1

Entonces, obtenemos,

yo = $\lim_{h\to0}h[f(1)+f(1+h)+f(1+2h)+...+f(1+(n-1)h)]$

= $\lim_{h\to0}h[1+(1+h)^2+(1+2h)^2+...+(1+(n-1)h)^2]$

= $\lim_{h\to0}h[1+(1+2h+h^2)+(1+4h+4h^2)+...+(1+2(n-1)h+(n-1)^2h^2)]$

= $\lim_{h\to0}h[n+2h(1+2+3+...+(n-1))+h^2(1^2+2^2+3^2+...+(n-1)^2)]$

= $\lim_{h\to0}h[n+2h(\frac{n(n-1)}{2})+h^2(\frac{n(n-1)(2n-1)}{6})]$

Ahora bien, si h −> 0, entonces n −> ∞. Entonces tenemos,

= $\lim_{n\to\infty}\frac{1}{n}[n+\frac{2}{n}(\frac{n(n-1)}{2})+\frac{1}{n^2}(\frac{n(n-1)(2n-1)}{6})]$

= $\lim_{n\to\infty}[1+(1-\frac{1}{n})+\frac{n^3}{6n^3}(1-\frac{1}{n})(2-\frac{1}{n})]$

= 1 + 1 + $\frac{2}{6}$

= 1 + 1 + $\frac{1}{3}$

= $\frac{7}{3}$

Por lo tanto, el valor de $\int_{1}^{2}x^2dx$ como límite de la suma es $\frac{7}{3}$ .

Pregunta 10. 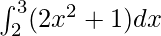$\int_{2}^{3}(2x^2+1)dx$

Solución:

Tenemos,

yo = $\int_{2}^{3}(2x^2+1)dx$

Sabemos,

$\int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]$ , donde h = $\frac{b-a}{n}$

Aquí a = 2, b = 3 y f(x) = 2x ² + 1.

=> h = 1/n

=> nh = 1

Entonces, obtenemos,

yo = $\lim_{h\to0}h[f(2)+f(2+h)+f(2+2h)+...+f(2+(n-1)h)]$

= $\lim_{h\to0}h[9+[2(2+h)^2+1]+[2(2+2h)^2+1]+...+[2(2+(n-1)h)^2+1]]$

= $\lim_{h\to0}h[9n+8h(1+2+3+...+(n-1))+2h^2(1^2+2^2+3^2+...(n-1)^2)]$

= $\lim_{h\to0}h[9n+8h(\frac{n(n-1)}{2})+2h^2(\frac{n(n-1)(2n-1)}{6})]$

Ahora bien, si h −> 0, entonces n −> ∞. Entonces tenemos,

= $\lim_{n\to\infty}\frac{1}{n}[9n+\frac{8}{n}(\frac{n(n-1)}{2})+\frac{2}{n^2}(\frac{n(n-1)(2n-1)}{6})]$

= $\lim_{n\to\infty}[9+\frac{4n^2}{n^2}(1-\frac{1}{n})+\frac{n^3}{3n^3}(1-\frac{1}{n})(2-\frac{1}{n})]$

= 9 + 4 + $\frac{2}{3}$

= $\frac{41}{3}$

Por lo tanto, el valor de $\int_{2}^{3}(2x^2+1)dx$ como límite de la suma es $\frac{41}{3}$ .

Pregunta 11. 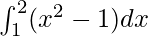$\int_{1}^{2}(x^2-1)dx$

Solución:

Tenemos,

yo = $\int_{1}^{2}(x^2-1)dx$

Sabemos,

$\int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]$ , donde h = $\frac{b-a}{n}$

Aquí a = 1, b = 2 y f(x) = x ² − 1.

=> h = 1/n

=> nh = 1

Entonces, obtenemos,

yo = $\lim_{h\to0}h[f(1)+f(1+h)+f(1+2h)+...+f(1+(n-1)h)]$

= $\lim_{h\to0}h[(1^2-1)+[(1+h)^2-1]+[(1+2h)^2-1]+...+[(1+(n-1)h)^2-1)]$

= $\lim_{h\to0}h[0+2h(1+2+3+...+(n-1))+h^2(1^2+2^2+3^2+...+(n-1)^2)]$

= $\lim_{h\to0}h[2h(\frac{n(n-1)}{2})+h^2(\frac{n(n-1)(2n-1)}{6})]$

Ahora bien, si h −> 0, entonces n −> ∞. Entonces tenemos,

= $\lim_{n\to\infty}\frac{1}{n}[\frac{2}{n}(\frac{n(n-1)}{2})+\frac{1}{n^2}(\frac{n(n-1)(2n-1)}{6})]$

= $\lim_{n\to\infty}[\frac{n^2}{n^2}(1-\frac{1}{n})+\frac{n^3}{6n^3}(1-\frac{1}{n})(2-\frac{1}{n})]$

= 1 + $\frac{2}{6}$

= 1 + $\frac{1}{3}$

= $\frac{4}{3}$

Por lo tanto, el valor de $\int_{1}^{2}(x^2-1)dx$ como límite de la suma es $\frac{4}{3}$ .