Determine el orden y el grado de la siguiente ecuación diferencial. Indique también si es lineal o no lineal (Pregunta 14-26)
Pregunta 14. 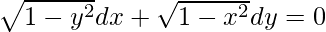
Solución :
Tenemos,
Orden de función:
Como el orden más alto de la derivada de la función es 1 (es decir, dy/dx)
Entonces, el orden de la derivada es igual a 1.
Grado de función:
Como la potencia de la derivada de mayor orden de la función es 1 (es decir, la potencia de dy/dx es 1)
Entonces, el grado de función es 1.
Lineal o no lineal:
La ecuación dada no es lineal.
Pregunta 15. 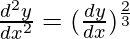
Solución:
Tenemos,
Al elevar al cubo ambos lados, tenemos
Orden de función:
El orden más alto de la derivada de la función es 2. (es decir,
)
Entonces, el orden de la derivada es igual a 2.
Grado de función:
Como la potencia de la derivada de mayor orden de la función es 3 (es decir, la potencia de
es 3)
Entonces, el grado de función es 3.
Lineal o no lineal:
La ecuación dada no es lineal.
Pregunta 16. 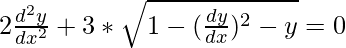
Solución:
Tenemos,
Elevando al cuadrado ambos lados, tenemos
Orden de función:
Como el orden más alto de la derivada de la función es 2. (es decir,
)
Entonces, el orden de la función es igual a 2.
Grado de función:
Como la potencia de la derivada de mayor orden de la función es 2 (es decir, la potencia de
es 2)
Entonces, el grado de la función es igual a 2.
Lineal o no lineal:
La ecuación dada no es lineal.
Pregunta 17. ![Rendered by QuickLaTeX.com 5\frac{d^2y}{dx^2}=[1+(\frac{dy}{dx})^2]^\frac{3}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-65b0146e0cf5a63c7ebc94fb0192e791_l3.png)
Solución:
Tenemos,
Uno elevando al cuadrado ambos lados, tenemos
Orden de función:
Como el orden más alto de la derivada de la función es 2 (es decir,
)
Entonces, el orden de la función es igual a 2.
Grado de función:
Como la potencia de la derivada de mayor orden de la función es 2 (es decir, la potencia de
es 2)
Entonces, el grado de la función es igual a 2.
Lineal o no lineal:
La ecuación dada no es lineal.
Pregunta 18. 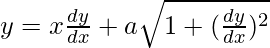
Solución:
Tenemos,
Al elevar al cuadrado ambos lados, obtenemos
Orden de función:
Como el mayor orden de derivada de la función es 1,
Entonces, el Orden de la función es igual a 1.
Grado de función:
Como la potencia de la derivada de mayor orden de la función es 2 (es decir, la potencia de dy/dx es 2)
Entonces, el grado de la función es igual a 2.
Lineal o no lineal:
La ecuación dada no es lineal.
Pregunta 19. 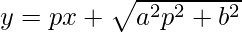 , donde p = dy/dx
, donde p = dy/dx
Solución:
Tenemos
, donde p = dy/dx
Orden de función:
Como el orden más alto de la derivada de la función es 1
Entonces, el Orden de la función es igual a 1.
Grado de función:
Como la potencia de la derivada de mayor orden de la función es 2 (es decir, la potencia de dy/dx es 2)
Entonces, el grado de la función es igual a 2.
Lineal o no lineal:
La ecuación dada no es lineal.
Pregunta 20: dy/dx + e y = 0
Solución :
Tenemos,
dy/dx + e y = 0
Orden de función:
Como el mayor orden de derivada de la función es 1
Entonces, el Orden de la función es igual a 1.
Grado de función:
Como la potencia de la derivada de mayor orden de la función es 1 (es decir, la potencia de dy/dx es 1)
Entonces, el Grado de la función es igual a 1.
Lineal o no lineal:
La ecuación dada no es lineal.
Pregunta 21. 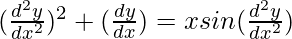
Solución :
Tenemos,
Orden de función:
Como el mayor orden de derivada de la función es 2
Entonces, el orden de la derivada es igual a 2.
Grado de función:
no es una función polinomial. Entonces el grado no se puede definir.
Por lo tanto, el grado de función no está definido.
Lineal o no lineal:
La ecuación dada no es lineal.
Pregunta 22. (y”) 2 + (y’) 3 + seno = 0
Solución:
Tenemos,
(y”) 2 + (y’) 3 + seno = 0
Dónde
Orden de función:
El orden más alto de la derivada de la función es 2. (es decir, y”)
Entonces, el orden de la derivada es igual a 2.
Grado de función
Como la potencia de la derivada de mayor orden de la función es 2 (es decir, la potencia de y” es 2)
Entonces, el grado de función es 2.
Lineal o no lineal:
La ecuación dada no es lineal.
Pregunta 23.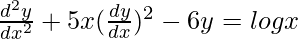
Solución:
Tenemos,
Orden de función:
Como el mayor orden de derivada de la función es 2.
Entonces, el orden de la función es igual a 2.
Grado de función:
Como la potencia de la derivada de mayor orden de la función es 1 (es decir, la potencia de
es 1)
Entonces, el Grado de la función es igual a 1.
Lineal o no lineal:
La ecuación dada no es lineal.
Pregunta 24. 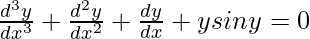
Solución:
Tenemos,
Orden de función:
Como el mayor orden de derivada de la función es 3
Entonces, el Orden de la función es igual a 3.
Grado de función:
Como la potencia de la derivada de mayor orden de la función es 1 (es decir, la potencia de
es 1)
Entonces, el Grado de la función es igual a 1.
Lineal o no lineal:
La ecuación dada es lineal.
Pregunta 25. 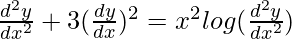
Solución:
Tenemos,
Orden de función:
Como el mayor orden de derivada de la función es 2.
Entonces, el orden de la función es igual a 2.
El grado de función:
no es una función polinomial. Entonces el grado no se puede definir.
Por lo tanto, el grado de función no está definido.
Lineal o no lineal:
La ecuación dada no es lineal.
Pregunta 26. 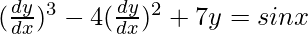
Solución:
Tenemos,
Orden de función:
Como el mayor orden de derivada de la función es 1
Entonces, el Orden de la función es igual a 1.
Grado de función:
Como la potencia de la derivada de mayor orden de la función es 3 (es decir, la potencia de dy/dx es 3)
Entonces, el grado de la función es igual a 3.
Lineal o no lineal:
La ecuación dada no es lineal.
Publicación traducida automáticamente
Artículo escrito por vivekray59 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA