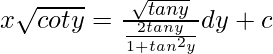Resuelve las siguientes ecuaciones diferenciales:
Pregunta 24. (2x – 10y 3 )(dy/dx) + y = 0
Solución:
Tenemos,
(2x – 10y 3 )(dy/dx) + y = 0
(2x – 10y 3 )(dy/dx) = -y
(dx/dy) = -(2x – 10y 3 )/y
(dx/dy) + 2x/y = 10y 2 ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dx/dy) + Px = Q
Donde, P = 2/año, Q = 10y 2
Asi que,
SI = e ∫Pdy
= e ∫(2/y)dy
= e 2log|y|
= y 2
La solución de una ecuación diferencial es,
x(SI) = ∫Q(SI)dy + c
x(y 2 ) = ∫(10y 2 )(y 2 )dy + c
xy 2 = 10(y 5 /5) + c
x = 2y 3 + cy -2
Esta es la solución requerida.
Pregunta 25. (x + tany)dy = sin2ydx
Solución:
Tenemos,
(x + tany)dy = sen2ydx
(dx/dy) = (x + tany)/sen2y
(dx/dy) – cosec2y.x = tany/sen2y ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dx/dy) + Px = Q
Donde, P = -cosec2y, Q = tany/sen2y
Entonces, SI = e ∫Pdy
= e ∫-cosec2ydy
=
=
= √coti
La solución de una ecuación diferencial es,
x(SI) = ∫Q(SI)dy + c
x(√coty) = ∫(tany/sen2y).(√coty)dy + c
Sea tany = z
Al diferenciar ambos lados tenemos,
segundo 2 ydx = dz
(x/√tany) = (1/2)∫dz/√z + c
(x/√tany) = (1/2)(2√z) + c
x = (√tany)(√tany) + c(√tany)
x = tany + c(√tany)
Esta es la solución requerida.
Pregunta 26. dx + xdy = e -y seg 2 ydy
Solución:
Tenemos,
dx + xdy = e -y segundo 2 ydy
(x – e -y segundo 2 y)dy = -dx
(dx/dy) = (e -y seg 2 y-x) ………..(i)
La ecuación anterior es una ecuación diferencial lineal de la forma
(dx/dy) + Px = Q
Donde, P = 1, Q = e -y seg 2 y
Entonces, SI = e ∫Pdy
= e ∫dy
= e y
La solución de una ecuación diferencial es,
x(SI) = ∫Q(SI)dy + c
x(e y ) = ∫e -y sce 2 ye y dy + c
x(e y ) = ∫seg 2 ydy + c
x(e y ) = tany + c
x = (tany + c)e -y
Esta es la solución requerida.
Pregunta 27. (dy/dx) = ytanx – 2senx
Solución:
Tenemos,
(dy/dx) = ytanx – 2senx
(dy/dx) – ytanx = -2senx ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Py = Q
Donde, P = -tanx, Q = senx
Asi que,
SI = e ∫Pdx
= e ∫-tanxdx
= e -log|secx|
= 1/segx
= cosx
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
y(cosx) = -2∫senx.(cosx)dx + c
ycosx = -∫2senx.cosxdx + c
Sea, senx = z
Al diferenciar ambos lados tenemos,
cosxdx = dz
ycosx = -2∫zdz + c
ycosx = -2(z 2 /2) + c
ycosx = -sen 2 xdx + c
y = secx(-sen 2 xdx + c)
Esta es la solución requerida.
Pregunta 28. (dy/dx) + ycosx = senx.cosx
Solución:
Tenemos,
(dy/dx) + ycosx = senx.cosx ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Py = Q
Donde, P = cosx, Q = senx.cosx
Asi que,
SI = e ∫Pdx
= e ∫cosxdx
= e senx
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
y(e senx ) = ∫(e senx )(senx.cosx)dx + c
Sea, senx = z
Diferenciando ambos lados obtenemos,
cosxdx = dz
y(e z ) = ∫ze z dz + c
y(e z ) = z∫e z dz – {(dz/dz)∫e z dz}dz
y(e z ) = ze z – ∫e z dz + c
y(e z ) = e z (z – 1) + c
y = (z – 1) + ce -z
y = (senx – 1) + ce -senx
Esta es la solución requerida.
Pregunta 29. (1 + x 2 )(dy/dx) – 2xy = (x 2 + 2)(x 2 + 1)
Solución:
Tenemos,
(1 + x 2 )(dy/dx) – 2xy = (x 2 + 2)(x 2 + 1)
(dy/dx) – 2xy/(1 + x 2 ) = (x 2 + 2) ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Py = Q
Donde, P = -2x/(1 + x 2 ), Q = (x 2 + 1)
Asi que,
SI = e ∫Pdx
=
= 1/(x2 +1 )
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
y.[1/(x 2 + 1)] = ∫[(x 2 + 2)/(x 2 + 1)]dx + c
y/(x 2 + 1) = ∫[1 + 1/(x 2 + 1)]dx + c
y/(x 2 + 1) = x + tan -1 x + c
y = (x 2 + 1)(x + tan -1 x + c)
Esta es la solución requerida.
Pregunta 30. senx(dy/dx) + ycosx = 2sen 2 xcosx
Solución:
Tenemos,
senx(dy/dx) + ycosx = 2sen 2 xcosx
(dy/dx) + ycotx = 2senx.cosx ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Py = Q
Donde, P = cotx, Q = 2senx.cosx
Asi que,
SI = e ∫Pdx
= e ∫cotxdx
= e log|senx|
= senx
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
y(senx) = ∫(2senx.cosx)senxdx + c
Sea, senx = z
Al diferenciar ambos lados tenemos,
cosxdx = dz
yz = 2∫z 2 + c
yz = (2/3)z 3 + c
y.senx = (2/3)sen 3 x + c
Esta es la solución requerida.
Pregunta 31. (x 2 – 1)(dy/dx) + 2(x + 2)y = 2(x + 1)
Solución:
Tenemos,
(x 2 – 1)(dy/dx) + 2(x + 2)y = 2(x + 1)
(dy/dx) + 2(x + 2)y/(x 2 – 1) = 2(x + 1)/(x 2 – 1)
(dy/dx) + 2(x + 2)y/(x 2 – 1) = 2/(x – 1) ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Py = Q
Donde, P = 2(x + 2)/(x 2 – 1), Q = 2/(x – 1)
Asi que,
SI = e ∫Pdx
=
= (x – 1) 3 /(x + 1)
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
y.[(x – 1) 3 /(x + 1)] = ∫[(x – 1) 3 /(x + 1)[{2/(x – 1)]dx + c
y.[(x – 1) 3 /(x + 1)] = (x 2 – 6x + 8log|x + 1|) + c
Esta es la solución requerida.
Pregunta 32. (dy/dx) + (2y/x) = cosx
Solución:
Tenemos,
(dy/dx) + (2y/x) = cosx ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Py = Q
Donde, P = 2/x, Q = cosx
Asi que,
SI = e ∫Pdx
= e ∫(2/x)dx
= e 2log|x|
= x2
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
y(x2 ) = ∫(x2 ).( cosx )dx + c
x 2 (y) = x 2 ∫cosxdx – ∫{(d/dx)x 2 ∫cosxdx}dx + c
x 2 y = x 2 senx – 2∫xsenxdx + c
x 2 y = x 2 senx – 2x∫sinxdx + 2∫{(dx/dx)∫sinxdx}dx + c
x 2 y = x 2 senx + 2xcosx – 2∫cosxdx + c
x 2 y = x 2 senx + 2xcosx – 2senx + c
Esta es la solución requerida.
Pregunta 33. (dy/dx) – y = xe x
Solución:
Tenemos,
(dy/dx) – y = xe x ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Py = Q
Donde, P = -1, Q = xe x
Asi que,
SI = e ∫Pdx
= e ∫-dx
= e- x
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
y(e -x ) = ∫(e -x )(xe x )dx + c
ye -x = ∫xdx + c
ye -x = (x 2 /2) + c
y = [(x 2 /2) + c].e x
Esta es la solución requerida.
Pregunta 34. (dy/dx) + 2y = xe 4x
Solución:
Tenemos,
(dy/dx) + 2y = xe 4x ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Py = Q
Donde, P = 2, Q = xe 4x
Asi que,
SI = e ∫Pdx
= e 2∫dx
= mi 2x
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
y(e 2x ) = ∫(e 2x ).(xe 4x )dx + c
y(e 2x ) = ∫xe 6x dx + c
y(e 2x ) = x∫e 6x dx – ∫{(dx/dx)∫e 6x dx}dx + c
mi 2x y = (xe 6x ) /6 – ∫(e 6x /6)dx + c
e 2x y = (xe 6x )/6 – e 6x /36 + c
y = (xe 4x )/6 – e 4x /36 + ce -2x
Esta es la solución requerida.
Pregunta 35. (x + 2y 2 )(dy/dx) = y, dado que cuando x = 2, y = 1
Solución:
Tenemos,
(x + 2y 2 )(dy/dx) = y
(dx/dy) = (x + 2y 2 )/y
(dx/dy) – (x/y) = 2y ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dx/dy) + Px = Q
Donde, P = 1/año, Q = 2 años
Asi que,
SI = e ∫Pdy
= e ∫-dy/y
= e -log|y|
= 1/año
La solución de una ecuación diferencial es,
x(SI) = ∫Q(SI)dy + c
x(1/y) = ∫(1/y)(2y)dy + c
(x/y) = 2∫dy + c
(x/y) = 2y + c
x = 2y 2 + cy
Dado que cuando x = 2, y = 1
2 = 2 + c
c = 0
x = 2y 2
Esta es la solución requerida.
Pregunta 36(i). Encuentre familias de un parámetro de curvas solución de la siguiente ecuación diferencial (dy/dx) + 3y = e mx , m es un número real dado
Solución:
Tenemos,
(dy/dx) + 3y = e mx ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Py = Q
Donde, P = 3, Q = e mx
Asi que,
SI = e ∫Pdx
= e ∫3dx
= mi 3x
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
y(e 3x ) = ∫(e 3x ).(e mx )dx + c
y(e 3x ) = ∫e (3+m)x dx + c
y(e 3x ) = e (m+3)x /(m + 3) + c
y = e mx /(m + 3) + c
Esta es la solución requerida.
Pregunta 36(ii). Encuentre familias de un parámetro de curvas solución de la siguiente ecuación diferencial (dy/dx) – y = cos2x
Solución:
Tenemos,
(dy/dx) – y = cos2x ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Py = Q
Donde, P = -1, Q = cos2x
Asi que,
SI = e ∫Pdx
= e -∫dx
= e- x
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
y(e -x ) = ∫(e -x ).(cos2x)dx + c
y(e -x ) = ∫e -x cos2xdx + c
Dejar,
A = ∫e -x cos2xdx
= e -x ∫cos2xdx – {(d/dx)e -x ∫cos2xdx}dx
= (e -x /2)sen2x + ∫(e -x /2)sen2xdx
=
(5/4)A = (e -x /2)(2sen2x – cos2x)
Esta es la solución requerida.
Pregunta 36(iii). Encuentre familias de un parámetro de curvas solución de la siguiente ecuación diferencial x(dy/dx) – y = (x + 1)e -x
Solución:
Tenemos,
x(dy/dx) – y = (x + 1)e -x
(dy/dx) – y/x = [(x + 1)/x]e -x ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Py = Q
Donde, P = -1/x, Q = [(x + 1)/x]e -x
Asi que,
SI = e ∫Pdx
= e -∫dx/x
= e -log|x|
= 1/x
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
y(1/x) = ∫[(x+1)/x]e -x (1/x)dx + c
y/x = ∫[1/x+1/x 2 ]e -x dx + c
Sea, (1/x)e -x = z
Al derivar ambos lados tenemos
-[1/x + 1/x2]e -x dx = dz
y/x = -∫dz + c
y/x = -z + c
y/x = -(e -x /x) + c
y = -e -x + cx
Esta es la solución requerida.
Pregunta 36(iv). Encuentre familias de un parámetro de curvas solución de la siguiente ecuación diferencial x(dy/dx) + y = x 4
Solución:
Tenemos,
x(dy/dx) + y = x 4
(dy/dx) + y/x = x 3 ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Py = Q
Donde, P = 1/x, Q = x 3
Asi que,
SI = e ∫Pdx
= e ∫dx/x
= e log|x|
= x
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
y(x) = ∫(x)(x 3 )dx + c
xy = ∫x 4 + c
xy = (x 5 /5) + c
y = (x 4 /5) + c/x
Esta es la solución requerida.
Pregunta 36(v). Encuentre familias de un parámetro de curvas solución de la siguiente ecuación diferencial (xlogx)(dy/dx) + y = logx
Solución:
Tenemos,
(xlogx)(dy/dx) + y = logx
(dy/dx) + y/xlogx = 1/x ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Py = Q
Donde, P = 1/xlogx, Q = 1/x
Asi que,
SI = e ∫Pdx
= e ∫dx/xlogx
Sea, logx = z
Al derivar ambos lados tenemos
dx/x = dz
= e ∫dz/z
= elog|z|
= z
=l ogx
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
y(logx) = ∫(1/x)(logx)dx + c
y(logx) = ∫zdz + c (Sean, logx=z y diferenciando ambos lados)
y(logx) = (z 2 /2) + c
y(logx) = (logx) 2 /2 + c
y = logx/2 + c/logx
Esta es la solución requerida.
Pregunta 36 (vi). Encuentre familias de un parámetro de curvas solución de la siguiente ecuación diferencial (dy/dx) – 2xy/(1 + x 2 ) = x 2 + 2
Solución:
Tenemos,
(dy/dx) – 2xy/(1 + x 2 ) = x 2 + 2 ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Py = Q
Donde, P = -2x/(1 + x 2 ), Q = x 2 + 2
Asi que,
SI = e ∫Pdx
= e -∫2xdx/(1+x2)
= e -log|1+x2|
= 1/(1+ x2 )
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
y[1/(1 + x 2 )] = ∫[1/(1 + x 2 )](x 2 + 2)dx + c
y/(1 + x 2 ) = ∫[(x 2 + 2)/(x 2 + 1)]dx + c
y/(1 + x 2 ) = ∫dx + ∫dx/(x 2 + 1) + c
y/(x 2 + 1) = x + tan -1 x + c
y = (x + tan -1 x + c)(x 2 + 1)
Esta es la solución requerida.
Pregunta 36 (vii). Encuentre familias de un parámetro de curvas solución de la siguiente ecuación diferencial (dy/dx) + ycosx = e senx cosx
Solución:
Tenemos,
(dy/dx) + ycosx = e senx cosx ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Py = Q
Donde, P = cosx, Q = e senx cosx
Asi que,
SI = e ∫Pdx
= e∫cosxdx
= e senx
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
y[(e senx ) = ∫(e senx )(e senx cosx)dx + c
Sea, senx = z
AL diferenciar ambos lados tenemos,
cosxdx = dz
ye z = ∫e 2z dz + c
ye z = (e 2z /2) + c
y = ez/2 + ce – z
y = (e sen x /2) + ce – sen x
Esta es la solución requerida.
Pregunta 36 (viii). Encuentre familias de un parámetro de curvas solución de la siguiente ecuación diferencial (x + y)(dy/dx) = 1
Solución:
Tenemos,
(x + y)(dy/dx) = 1
(dy/dx) = 1/(x + y)
(dx/dy) = (x + y)
(dx/dy) – x = y ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dx/dy) + Px = Q
Donde, P = -1, Q = y
Asi que,
SI = e ∫Pdy
= e -∫dy
= e- y
La solución de una ecuación diferencial es,
x(SI) = ∫Q(SI)dy + c
x(e -y ) = ∫(e -y )(y)dy + c
xe -y = y∫e -y dy – ∫{(dy/dy)∫e -y dy}dy + c
xe -y = -ye -y + ∫e -y + c
xe -y = -ye -y – e -y + c
xe -y + ye -y + e -y = c
e -y (x + y + 1) = c
(x + y + 1) = ce y
Esta es la solución requerida.
Pregunta 36(ix). Encuentre familias de un parámetro de curvas solución de la siguiente ecuación diferencial cos 2 x(dy/dx) = (tanx – y)
Solución:
Tenemos,
cos 2 x(dy/dx) = (tanx – y)
(dy/dx) = (tanx – y)/cos 2 x
(dy/dx) = tanx.seg 2 x – yseg 2 x
(dy/dx) + ysec 2 x = tanx.sec 2 x ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Py = Q
Donde, P = seg 2 x, Q = tanx.sec 2 x
Asi que,
SI = e∫Pdx
= e tanx
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
y(e tanx ) = ∫(e tanx )(tanx.sec 2 x)dx + c
Sea, tanx = z
Al diferenciar ambos lados tenemos,
seg 2 xdx = dz
y(e z ) = ∫ze z dz + c
y(e z ) = z∫e z dz – ∫{(dz/dz)∫e z dz}dz
y(e z ) = ze z – ∫e z dz + c
y(e z ) = ze z – e z + c
y = (z – 1) + ce -z
y = (tanx – 1) + ce -tanx
Esta es la solución requerida.
Pregunta 36(x). Encuentre familias de un parámetro de curvas solución de la siguiente ecuación diferencial e -y sec 2 ydy = dx + xdy
Solución:
Tenemos,
dx + xdy = e -y segundo 2 ydy
(x – e -y segundo 2 y)dy = -dx
(dx/dy) = (e -y seg 2 y – x)
(dx/dy) + x = e -y seg 2 y ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dx/dy) + Px = Q
Donde, P = 1, Q = e -y seg 2 y
Entonces, SI = e ∫Pdy
= e ∫dy
= e y
La solución de una ecuación diferencial es,
x(SI) = ∫Q(SI)dy + c
x(e y ) = ∫e -y sce 2 ye y dy + c
x(e y ) = ∫seg 2 ydy + c
x(e y ) =tany + c
x = (tan y + c)e -y
Esta es la solución requerida.
Pregunta 36(xi). Encuentre familias de un parámetro de curvas solución de la siguiente ecuación diferencial (xlogx)(dy/dx) + y = 2logx
Solución:
Tenemos,
(xlogx)(dy/dx) + y = 2logx
(dy/dx) + y/xlogx = 2/x ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Py = Q
Donde, P = 1/xlogx, Q = 2/x
Asi que,
SI = e ∫Pdx
= e ∫dx/xlogx
Sea, logx = z
Al derivar ambos lados tenemos
dx/x = dz
= e ∫dz/z
= elog|z|
= z
= logaritmo x
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
y(logx) = ∫(2/x)(logx)dx + c
y(logx) = 2∫zdz + c (Sea, logx = z y diferenciando ambos lados)
y(logx) = 2(z 2 /2) + c
y(logx) = (logx) 2 + c
y = logx + c/logx
Esta es la solución requerida.
Pregunta 36(xii). Encuentre familias de un parámetro de curvas solución de la siguiente ecuación diferencial x(dy/dx) + 2y = x 2 logx
Solución:
Tenemos,
x(dy/dx) + 2y = x 2 logx
(dy/dx) + 2y/x = xlogx ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Py = Q
Donde, P = 2/x, Q = xlogx
Asi que,
SI = e∫Pdx
= e 2∫dx/x
= e 2logx
= x2
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
y(x2 ) = ∫(x2 )( xlogx )dx + c
x 2 y = ∫x 3 logxdx + c
x 2 y = logx∫x 3 dx + ∫{(d/dx)logx∫x 3 dx}dx + c
x 2 y = (1/4)x 4 logx – (1/4)∫x 3 dx + c
x 2 y = (1/4)x 4 logx – (1/16)x 4 + c
y = (x2 / 16 )(4logx – 1) + c/ x2
Esta es la solución requerida.
Pregunta 37. Resuelve lo siguiente usando el problema de valor inicial:-
(i). y’ + y = e x , y(0) = (1/2)
Solución:
Tenemos,
y’ + y = e x
dy/dx + y = e x ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Py = Q
Donde, P = 1, Q = e x
Entonces, SI = e ∫Pdx
= e ∫dx
= e x
La solución de la ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
y(e x ) = ∫e x .e x dx + c
y(e x ) = (1/2)e 2x + c
En t = 0, y = (1/2)
(1/2)e 0 = (1/2)e 0 + c
c = 0
y(e x ) = (1/2)e 2x
y = (ex / 2)
Esta es la solución requerida.
(ii). x(dy/dx) – y = logx, y(1) = 0
Solución:
Tenemos,
x(dy/dx) – y = logx
(dy/dx) – y/x = logx/x ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Py = Q
Donde, P = -1/x, Q = logx/x
Asi que,
SI = e ∫Pdx
= e -∫dx/x
= e -log|x|
= 1/x
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
y(1/x) = ∫(1/x)(logx/x)dx + c
(y/x) = ∫(logx/x 2 )dx + c
(y/x) = logx∫(dx/x 2 ) – ∫{(d/dx)logx∫(dx/x 2 )}dx + c
(y/x) = -(logx/x) + ∫(dx/x 2 ) + c
(y/x) = -(logx/x) – (1/x) + c
En x = 1, y = 0
0 = -0 – 1 + c
c = 1
(y/x) = -(logx/x) – (1/x) + 1
y = x – 1 – logaritmo x
Esta es la solución requerida.
(iii). (dy/dx) + 2y = e -2x senx, y(0) = 0
Solución:
Tenemos,
(dy/dx) + 2y = e -2x senx ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Py = Q
Donde, P = 2, Q = e -2x senx
Asi que,
SI = e ∫Pdx
= e ∫2dx
= mi 2x
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
y(e 2x ) = ∫e -2x senx.(e 2x )dx + c
y(e 2x ) = ∫senxdx + c
y(e 2x ) = -cosx + c
En x = 0, y = 0
0 = -1 + c
c = 1
y(e 2x ) = 1 – cosx
Esta es la solución requerida.
(iv). x(dy/dx) – y = (x + 1)e -x , y(1) = 0
Solución:
Tenemos,
x(dy/dx) – y = (x + 1)e -x
(dy/dx) – (y/x) = [(x + 1)/x]e -x ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Py = Q
Donde, P = -(1/x), Q = [(x + 1)/x]e -x
Asi que,
SI = e ∫Pdx
= e -∫(dx/x)
= e -log(x)
= e log(1/x)
= 1/x
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
(y/x) = ∫[(1/x) + (1/x 2 )]e -x + c
Ya que, -∫[f(x) + f'(x)]e -x dx = f(x)e -x + c
(y/x) = -e -x /x + c
En x = 1, y = 0
0 = -e -1 + c
c = e- 1
(y/x) = -e -x /x + e -1
y = xe -1 – e -x
Esta es la solución requerida.
(v). (1 + y 2 )dx + (x – 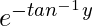 )dx = 0, y(0) = 0
)dx = 0, y(0) = 0
Solución:
Tenemos,
(1 + y 2 )(dx/dy) + x =
(dy/dx) + [1/(y 2 + 1)]x =
/(y 2 + 1) ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Px = Q
Donde, P = 1/(y 2 + 1), Q =
/(y 2 + 1)
Asi que,
SI = e ∫Pdy
= e tan-1y
La solución de una ecuación diferencial es,
x(SI) = ∫Q(SI)dy + c
x(
) = ∫[
/(y 2 + 1)]
dx + c
x(
) = ∫dy/(1 + y 2 ) + c
x(e tan-1y ) = tan -1 y + c
En x = 0, y = 0
0*e 0 = 0 + c
c = 0
x(
) = bronceado -1 y
Esta es la solución requerida.
(vi). (dy/dx) + ytanx = x 2 tanx + 2x, y(0) = 1
Solución:
Tenemos,
(dy/dx) + ytanx = x 2 tanx + 2x ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Py = Q
Donde, P = tanx, Q = x 2 tanx+2x
Asi que,
SI = e ∫Pdx
= e ∫tanxdx
= e log|secx|
= secx
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
y(segx) = ∫(x 2 tanx + 2x)segxdx + c
y(secx) = ∫(x 2 tanxsecx + 2xsecx)dx + c
y(segx) = ∫x 2 tanxsecxdx + 2∫xsecxdx + c
y(secx) = ∫x 2 tanxsecxdx + 2secx∫xdx – 2∫{(d/dx)secx∫xdx}dx + c
y(secx) = ∫x 2 tanxsecxdx + x 2 .secx – ∫x 2 tanxsecxdx + c
y(segx) = x 2 ,(segx)+c
En, x = 0, y = 1
1 = 0 + c
c = 1
y = x 2 + cos x
Esta es la solución requerida.
(vii). x(dy/dx) + y = xcosx + senx, y(π/2) = 1
Solución:
Tenemos,
x(dy/dx) + y = xcosx + senx
(dy/dx) + (y/x) = cosx + senx/x ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Py = Q
Donde, P = 1/x, Q = cosx + senx/x
Asi que,
SI = e ∫Pdx
= e ∫dx/x
= e log|x|
= x
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
y(x) = ∫(cosx + senx/x)(x)xdx + c
y(x) = ∫xcosxdx + ∫senxdx + c
xy = x∫cosxdx – ∫{(dx/dx)∫cosxdx}dx – cosx + c
xy = xsenx – ∫senxdx – cosx + c
xy = xsenx + cosx – cosx + c
xy = xsenx + c
En x = π/2, y = 1
π/2 = π/2sen(π/2) + c
c = 0
y = senx
Esta es la solución requerida.
(viii). (dy/dx) + ycotx = 4xcosecx, y(π/2) = 0
Solución:
Tenemos,
(dy/dx) + ycotx = 4xcosecx ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Py = Q
Donde, P = cotx, Q = 4xcosecx
Asi que,
SI = e ∫Pdx
= e ∫cotx.dx
= e log|senx|
= senx
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
y(senx) = 4∫(xcosecx)(senx)xdx + c
y(senx) = 4∫xdx + c
y(senx) = 4(x 2 /2) + c
y(senx) = 2x 2 + c
En x = π/2, y = 0,
0 = 2(π/2) 2 + c
c = -π 2 /2
y(senx) = 2x 2 – π 2 /2
Esta es la solución requerida.
(ix). (dy/dx) + 2ytanx = senx, y = 0 cuando x = π/3
Solución:
Tenemos,
(dy/dx) + 2ytanx = senx ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Py = Q
Donde, P = 2tanx, Q = senx
Entonces, SI = e ∫Pdx
= e ∫2tanxdx
= e 2log|secx|
= segundo 2 x
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
y.seg 2 x = ∫senx.seg 2 xdx + c
y.seg 2 x = ∫tanx.segxdx + c
y.seg 2 x = secx+c
En x = π/3, y = 0,
0 = segundo 2 (π/3) + c
c = -2
y.seg 2 x = secx – 2
y = cosx – 2cos 2 x
Esta es la solución requerida.
(X). (dy/dx) – 3ycotx = sen2x, y = 2 cuando x = π/2
Solución:
Tenemos,
(dy/dx) – 3ycotx = sen2x ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Py = Q
Donde, P = -3cotx, Q = sen2x
Entonces, SI = e ∫Pdx
= e ∫-3cotxdx
= e -3log|senx|
= cosec 3 x
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
y.(cosec 3 x) = 2∫(cosec 3 x).(sen2x)dx + c
y.(cosec 3 x) = 2∫cotx.cosecxdx + c
y.(coseg 3 x) = -2cosesx +c
y = -2sen 2 x + c.sen 3 x
En x = π/2, y = 2.
2 = -2sen 2 (π/2) + c.sen 3 (π/2)
c = 4
y = c.sen 3 x – 2sen 2 x
Esta es la solución requerida.
(xi). (dy/dx) + ycotx = 2cosx, y(π/2) = 0
Solución:
Tenemos,
(dy/dx) + ycotx = 2cosx ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Py = Q
Donde, P = cotx, Q = 2cosx
Entonces, SI = e ∫Pdx
= e ∫cotxdx
= e log|senx|
= senx
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
y.(senx) = ∫(senx).(2cosx)dx + c
y.(senx) = 2∫senx.cosxdx + c
y.(senx) = ∫sen2xdx + c
y.(senx) = -(cos2x/2) + c
En x = π/2, y = 0
0 = -cos(π)/2 + c
do = -(1/2)
y.(senx) = -(cos2x/2) – (1/2)
2y(senx) = -(1 + cos2x)
2y(senx) = -2cos 2 x
y = -cotx.cosx
Esta es la solución requerida.
(xii). dy = cosx(2 – ycosecx)dx,
Solución:
Tenemos,
dy = cosx(2 – ycosecx)dx
(dy/dx) = -ycotx + 2cosx
(dy/dx) + ycotx = 2cosx ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Py = Q
Donde, P = cotx, Q = 2cosx
Asi que,
SI = e ∫Pdx
= e ∫cotxdx
= e log|senx|
= senx
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
y(senx) = 2∫cosx.(senx)dx + c
ysenx = ∫2cosx.senxdx + c
ysenx = ∫sen2x + c
ysenx = -(cos2x/2) + c
Esta es la solución requerida.
Pregunta 38. x(dy/dx) + 2y = x 2
Solución:
Tenemos,
x(dy/dx) + 2y = x 2
(dy/dx) + 2y/x = x ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Py = Q
Donde, P = 2/x, Q = x
Entonces, SI = e ∫Pdx
= e 2∫dx/x
= e 2logx
= x2
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
yx 2 = ∫x2.xdx + c
yx 2 = ∫x 3 dx + c
x 2 y = (x 4 /4) + c
y = (x1/4) + cx -2
Esta es la solución requerida.
Pregunta 39. (dy/dx) – y = cosx
Solución:
Tenemos,
(dy/dx) – y = cosx ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Py = Q
Donde, P = -1, Q = cosx
Entonces, SI = e ∫Pdx
= e -∫dx
= e- x
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
y(e -x ) = ∫cosx.e -x dx + c
Sea, I = ∫cosx.e -x dx
yo = e -x ∫cosxdx – ∫{(d/dx)e -x ∫cosxdx}dx
I = e -x senx + ∫e -x senxdx
yo = e -x senx + e -x ∫sinxdx-∫{(d/dx)e -x ∫sinxdx}dx
I = e -x senx – e -x cosx-∫e -x cosxdx
2I = e -x (senx – cosx)
I = (e -x /2)(senx – cosx)
y(e -x ) = (e -x /2)(senx – cosx) + c
y = (1/2)(senx-cosx) + ce x
Esta es la solución requerida.
Pregunta 40. (y + 3x 2 )(dx/dy) = x
Solución:
Tenemos,
(y + 3x 2 )(dx/dy) = x
(dy/dx) = (y + 3x 2 )/x
(dy/dx) – y/x = 3x ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dy/dx) + Py = Q
Donde, P = -1/x, Q = 3x
Entonces, SI = e ∫Pdx
= e -∫dx/x
= e -logx
= 1/x
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
y(1/x) = 3∫x.(1/x)dx + c
y(1/x) = 3∫dx + c
y/x = 3x + c
Esta es la solución requerida.
Pregunta 41. Hallar una solución particular de la ecuación diferencial (dx/dy) + xcoty = y 2 coty + 2y, dado que x = 0, cuando y = π/2
Solución:
Tenemos,
(dx/dy) + xcoty = y 2 coty + 2y ………..(i)
La ecuación dada es una ecuación diferencial lineal de la forma
(dx/dy) + Px = Q
Donde, P = coty, Q = y 2 coty + 2y
Asi que,
SI = e ∫Pdy
= e ∫cotydy
= e log|seny|
= seno
La solución de una ecuación diferencial es,
x(SI) = ∫Q(SI)dy + c
x(seno) = ∫(y 2 coty + 2y)senody + c
x(seny) = ∫(y 2 acogedor + 2xseny)dy + c
x(seno) = y 2 ∫cosydx – {(d/dy)y 2 ∫cosydy}dy + ∫2ysinydy + c
x(seny) = y 2 seny – ∫2ysinydy + ∫2ysinydy + c
x(seno) = y 2 seno + c
En x = 0, y = π/2
0 = (π/2) 2 sen(π/2) + c
c = -π 2 /4
x(seno) = y 2 seno – π 2 /4
Esta es la solución requerida.
Publicación traducida automáticamente
Artículo escrito por vivekray59 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA