Clase 12 Soluciones RD Sharma – Capítulo 22 Ecuaciones diferenciales – Ejercicio 22.10 | Serie 1

Posted on by Rudeus Greyrat

Resuelve las siguientes ecuaciones diferenciales:

Pregunta 1. dy/dx + 2y = e 3x

Solución:

Tenemos,

dy/dx + 2y = e 3x  ………..(i)

La ecuación dada es una ecuación diferencial lineal de la forma

(dy/dx) + Py = Q

Donde, P = 2, Q = e 3x

Entonces, SI = e ∫Pdx

= e ∫2dx

= mi 2x

La solución de la ecuación diferencial es,

y(SI) = ∫Q(SI)dx + c

y(e 2x ) = ∫e 3x .e 2x dx + c

y(e 2x ) = (1/5)e 5x + c

y = (e 3x /5) + ce -2x

Por lo tanto, esta es la solución requerida.

Pregunta 2. 4(dy/dx) + 8y = 5e -3x

Solución:

Tenemos,

4(dy/dx) + 8y = 5e -3x 

(dy/dx) + 2y = (5/4)e -3x  ………..(i)

La ecuación dada es una ecuación diferencial lineal de la forma

(dy/dx) + Py = Q

Donde, P = 2, Q = (5/4)e -3x

Entonces, SI = e ∫Pdx

= e ∫2dx

= mi 2x

La solución de la ecuación diferencial es,

y(SI) = ∫Q(SI)dx + c

y(e 2x ) = (5/4)∫e -3x .e 2x dx + c

y(e 2x ) = (5/4)∫e -x dx + c

y = -(5/4)e -3x + ce -2x

Esta es la solución requerida.

Pregunta 3. (dy/dx) + 2y = 6e x

Solución:

Tenemos,

(dy/dx) + 2y = 6e x ………..(i)

La ecuación dada es una ecuación diferencial lineal de la forma

(dy/dx) + Py = Q

Donde, P = 2, Q = 6e x

Entonces, SI = e ∫Pdx

= e ∫2dx

= mi 2x

La solución de una ecuación diferencial es,

y(SI) = ∫Q(SI)dx + c

y(e 2x ) = ∫6e x .e 2x dx + c

y(e 2x ) = 6∫e 3x dx + c

y(e 2x ) = 2e 3x + c

y = 2e x + ce -2x

Esta es la solución requerida.

Pregunta 4. (dy/dx) + y = e -2x

Solución:

Tenemos,

(dy/dx) + y = e -2x ………..(i)

La ecuación dada es una ecuación diferencial lineal de la forma

(dy/dx) + Py = Q

Donde, P = 1, Q = e -2x

Entonces, SI = e ∫Pdx

= e ∫dx

= e x

La solución de una ecuación diferencial es,

y(SI) = ∫Q(SI)dx + c

y(e x ) = ∫e -2x .e x dx + c

y(e x ) = ∫e -x dx + c

y(e x ) = -e -x + c

y = -e -2x + ce -x

Esta es la solución requerida.

Pregunta 5. x(dy/dx) = x + y

Solución:

Tenemos,

x(dy/dx) = x + y

(dy/dx) = 1 + (y/x)

(dy/dx) – (y/x) = 1 ………..(i)

La ecuación dada es una ecuación diferencial lineal de la forma

(dy/dx) + Py = Q

Donde, P = (-1/x), Q = 1

Entonces, SI = e ∫Pdx

= e -∫(dx/x)

= e -log(x)

= e log(1/x)

= (1/x)

La solución de una ecuación diferencial es,

y(SI) = ∫Q(SI)dx + c

y(1/x) = ∫(1/x)dx + c

(y/x) = registro|x| +c

y = xlog|x| + CX

Esta es la solución requerida.

Pregunta 6. (dy/dx) + 2y = 4x

Solución:

Tenemos,

(dy/dx) + 2y = 4x ………..(i)

La ecuación dada es una ecuación diferencial lineal de la forma

(dy/dx) + Py = Q

Donde, P = 2, Q = 4x

Asi que,

SI = e ∫Pdx

= e ∫2dx

= mi 2x

La solución de una ecuación diferencial es,

y(SI) = ∫Q(SI)dx + c

y(e 2x ) = ∫4x.e 2x dx + c

y(e 2x ) = 4x∫e 2x dx – 4∫{(dx/dx)∫e 2x dx}dx + c

y(e 2x ) = 2xe 2x – 2∫e 2x dx + c

y(e 2x ) = 2xe 2x – e 2x + c

y = (2x – 1) + ce -2x

Esta es la solución requerida.

Pregunta 7. x(dy/dx) + y = xe x

Solución:

Tenemos,

x(dy/dx) + y = xe x

(dy/dx) + (y/x) = e x  ………..(i)

La ecuación dada es una ecuación diferencial lineal de la forma

(dy/dx) + Py = Q

Donde, P = (1/x), Q = e x

Asi que,

SI = e ∫Pdx

= e ∫(dx/x)

= e log(x)

= x

La solución de una ecuación diferencial es,

y(SI) = ∫Q(SI)dx + c

y(x) = ∫xe x dx + c

xy = x∫e x dx – {(dx/dx)∫e x dx}dx + c

xy = xe x – ∫e x dx + c

xy = xe x – e x + c

y=\frac{x-1}{x}e^x+\frac{c}{x}

Esta es la solución requerida.

Pregunta 8. (dy/dx) + [4x/(x 2 + 1)]y = -1/(x 2 + 1) 2

Solución :

Tenemos,

(dy/dx) + [4x/(x 2 + 1)]y = -1/(x 2 + 1) 2    ………..(i)

La ecuación dada es una ecuación diferencial lineal de la forma

(dy/dx) + Py = Q

Donde, P = [4x/(x 2 + 1)], Q = -1/(x 2 + 1) 2

Asi que,

SI = e ∫Pdx

=e^{∫\frac{4x}{x^2+1}dx}

=e^{2log|x^2+1|}

= (x 2 + 1) 2

La solución de una ecuación diferencial es,

y(SI) = ∫Q(SI)dx + c

y(x 2 + 1) 2 = ∫-[1/(x 2 + 1) 2 ](x 2 + 1) 2 dx + c

y(x 2 + 1) 2 = -∫dx + c

y(x 2 + 1) 2 = -x + c

y = -x/(x 2 + 1) 2 + c/(x 2 + 1) 2

Esta es la solución requerida.

Pregunta 9. x(dy/dx) + y = xlogx

Solución:

Tenemos,

x(dy/dx) + y = xlogx

(dy/dx) + (y/x) = logx ………..(i)

La ecuación dada es una ecuación diferencial lineal de la forma

(dy/dx) + Py = Q

Donde, P = (1/x), Q = logx

Asi que,

SI = e ∫Pdx

= e ∫(dx/x)

= e log(x)

= x

La solución de una ecuación diferencial es,

y(SI) = ∫Q(SI)dx + c

y(x) = ∫x.logxdx + c

xy = logx∫xdx – {(d/dx)logx∫xdx}dx + c

xy = (x2 / 2 )logx – ∫(1/x)(x2 / 2 ) + c

xy = (x2 / 2 )logx – (1/2)∫xdx + c

xy = (x2 / 2 )logx – (x2 / 4 ) + c

y = (x/2)logx – (x/4) + (c/x)

Esta es la solución requerida.

Pregunta 10. x(dy/dx) – y = (x – 1)e x

Solución:

Tenemos,

x(dy/dx) – y = (x – 1)e x

(dy/dx) – (y/x) = [(x – 1)/x]e x  ………..(i)

La ecuación dada es una ecuación diferencial lineal de la forma

(dy/dx) + Py = Q

Donde, P = -(1/x), Q = [(x – 1)/x]e x

Asi que,

SI = e ∫Pdx

= e -∫(dx/x)

= e -log(x)

= e log(1/x)

= 1/x

La solución de una ecuación diferencial es,

y(SI) = ∫Q(SI)dx + c

y(\frac{1}{x})=∫(\frac{x-1}{x})e^x.(\frac{dx}{x})+c

(y/x) = ∫[(1/x) – (1/x 2 )]e x + c

Ya que, ∫[f(x) + f'(x)]e x dx = f(x)e x + c

(y/x) = (e x /x) + c

y = e x + xc

Esta es la solución requerida.

Pregunta 11. (dy/dx) + y/x = x 3

Solución:

Tenemos,

(dy/dx) + y/x = x 3     ………..(i)

La ecuación dada es una ecuación diferencial lineal de la forma

(dy/dx) + Py = Q

Donde, P = 1/x, Q = x 3

Entonces, SI = e ∫Pdx

= e ∫dx/x

= elogx

= x

La solución de una ecuación diferencial es,

y(SI) = ∫Q(SI)dx + c

yx = ∫x 3 .xdx + c

yx = ∫x 4 dx + c

yx = (x 5 /5) + c

y = (x 4 /5) + c/x

Esta es la solución requerida.

Pregunta 12. (dy/dx) + y = senx

Solución:

Tenemos,

(dy/dx) + y = senx ………..(i)

La ecuación dada es una ecuación diferencial lineal de la forma

(dy/dx) + Py = Q

Donde, P = 1, Q = senx

Entonces, SI = e ∫Pdx

= e ∫dx

= e x

La solución de una ecuación diferencial es,

y(SI) = ∫Q(SI)dx + c

y(e x ) = ∫senx.e x dx + c

Sea, I = ∫senx.e x dx

yo = e x ∫sinxdx – ∫{(d/dx)e x ∫sinxdx}dx

yo = -e x cos + ∫e x cosxdx

yo = -e x cosx + e x ∫cosxdx – ∫{(d/dx)e x ∫cosxdx}dx

I = -e x cosx + e x senx – ∫e x senxdx

2I = e x (senx – cosx)

I = (e x /2)(senx – cosx)

y(e x ) = (e x /2)(senx – cosx) + c

y = (1/2)(senx – cosx) + ce -x

Esta es la solución requerida.

Pregunta 13. (dy/dx) + y = cosx

Solución :

Tenemos,

(dy/dx) + y = cosx ………..(i)

La ecuación dada es una ecuación diferencial lineal de la forma

(dy/dx) + Py = Q

Donde, P = 1, Q = cosx

Entonces, SI = e ∫Pdx

= e ∫dx

= e x

La solución de una ecuación diferencial es,

y(SI) = ∫Q(SI)dx + c

y(e x ) = ∫cosx.e x dx + c

Sea, I = ∫cosx.e x dx

yo = e x ∫cosxdx – ∫{(d/dx)e x ∫cosxdx}dx

I = e x senx – ∫e x senxdx

yo = e x senx – e x ∫sinxdx + ∫{(d/dx)e x ∫sinxdx}dx

yo = e x senx + e x cosx – ∫e x cosxdx

2I = e x (cosx + senx)

I = (e x /2)(cosx + senx)

y(e x ) = (e x /2)(cosx + senx) + c

y = (1/2)(cosx + senx) + ce -x

Esta es la solución requerida.

Pregunta 14. (dy/dx) + 2y = senx

Solución:

Tenemos,

(dy/dx) + 2y = senx ………..(i)

La ecuación dada es una ecuación diferencial lineal de la forma

(dy/dx) + Py = Q

Donde, P = 2, Q = senx

Entonces, SI = e ∫Pdx

= e ∫2dx

= mi 2x

La solución de una ecuación diferencial es,

y(SI) = ∫Q(SI)dx + c

y(e 2x ) = ∫senx.e 2x dx + c

Sea, I = ∫senx.e 2x dx

yo = e 2x ∫sinxdx – {(d/dx)e 2x ∫sinxdx}dx

I = -e 2x cosx + 2∫e 2x cosdx

I = -e 2x cosx + 2e 2x ∫cosxdx – 2{(d/dx)e 2x ∫cosxdx}dx

I = -e 2x cosx + 2e 2x senx – 4∫e 2x senxdx

5I = e 2x (2senx – cosx)

yo = (e 2x /5)(2senx – cosx)

y(e 2x ) = (e 2x /5)(2senx – cosx) + c

y = (1/5)(2senx – cosx) + ce -2x

Esta es la solución requerida.

Pregunta 15. (dy/dx) – ytanx = -2senx

Solución:

Tenemos,

(dy/dx) – ytanx = -2senx ………..(i)

La ecuación dada es una ecuación diferencial lineal de la forma

(dy/dx) + Py = Q

Donde, P = -tanx, Q = senx

Asi que, 

SI = e ∫Pdx

= e ∫-tanxdx

= e -log|secx|

= 1/segx

La solución de una ecuación diferencial es,

y(SI) = ∫Q(SI)dx + c

y(1/segx) = -2∫senx.(1/segx)dx + c

ycosx = -∫2senx.cosxdx + c

ycosx = -∫sen2xdx + c

ycosx = (cos2x/2) + c

y = (cos2x/cosx) + (c/cosx)

Esta es la solución requerida.

Pregunta 16. (1 + x 2 )(dy/dx) + y = tan -1 x

Solución:

Tenemos,

(1 + x 2 )(dy/dx) + y = tan -1 x

(dy/dx) + [y/(1 + x 2 )] = tan -1 x/(1 + x 2 ) ………..(i)

La ecuación dada es una ecuación diferencial lineal de la forma

(dy/dx) + Py = Q

Donde, P = 1/(1 + x 2 ), Q = tan -1 x/(1 + x 2 )

Asi que,

SI = e ∫Pdx

=e^{∫\frac{dx}{1+x^2}}

=e^{tan^{-1}x}

La solución de una ecuación diferencial es,

y(SI) = ∫Q(SI)dx + c

y(e^{tan^{-1}x})=∫\frac{tan^{-1}x}{1+x^2}e^{tan^{-1}x}dx+c

Sea, tan -1 x = z

Al diferenciar ambos lados obtenemos,

dx/(1 + x 2 ) = dz

y(e z ) = ∫ze z dz + c

y(e z ) = z∫e z dz – {(dz/dz)∫e z dz}dz

y(e z ) = ze z – ∫ e z dz + c

y(e z ) = e z (z – 1) + c

y = (z – 1) + ce -z

y=(tan^{-1}x-1)+ce^{tan^{-1}x}

Esta es la solución requerida.

Pregunta 17. (dy/dx) + ytanx = cosx

Solución:

Tenemos,

(dy/dx) + ytanx = cosx ………..(i)

La ecuación dada es una ecuación diferencial lineal de la forma

(dy/dx) + Py = Q

Donde, P = tanx, Q = cosx

Entonces, SI = e ∫Pdx

= e ∫tanxdx

= e log|secx|

= secx

La solución de una ecuación diferencial es,

y(SI) = ∫Q(SI)dx + c

y.secx = ∫cosx.secxdx + c

y.secx = ∫dx + c

y.secx = x + c

y = xcosx + c.cosx

Esta es la solución requerida.

Pregunta 18. (dy/dx) + ycotx = x 2 cotx + 2x

Solución:

Tenemos,

(dy/dx) + ycotx = x 2 cotx + 2x ………..(i)

La ecuación dada es una ecuación diferencial lineal de la forma

(dy/dx) + Py = Q

Donde, P = cotx, Q = x 2 cotx + 2x

Asi que,

SI = e ∫Pdx

= e ∫cotxdx

= e log|senx|

= senx

La solución de una ecuación diferencial es,

y(SI) = ∫Q(SI)dx + c

y(senx) = ∫(x 2 cotx + 2x)senxdx + c

y(senx) = ∫(x 2 cosx + 2xsenx)dx + c

y(senx) = x 2 ∫cosxdx – {(d/dx)x 2 ∫cosxdx}dx + ∫2xsenxdx + c

y(senx) = x 2 senx – ∫2xsenxdx + ∫2xsenxdx + c

y(senx) = x 2 senxdx + c

Esta es la solución requerida.

Pregunta 19. (dy/dx) + ytanx = x 2 cos 2 x

Solución:

Tenemos,

(dy/dx) + ytanx = x 2 cos 2 x ………..(i)

La ecuación dada es una ecuación diferencial lineal de la forma

(dy/dx) + Py = Q

Donde, P = tanx, Q = x 2 cos 2 x

Asi que,

SI = e ∫Pdx

= e ∫tanxdx

= e log|secx|

= secx

La solución de una ecuación diferencial es,

y(SI) = ∫Q(SI)dx + c

y(secx) = ∫secx.(x 2 .cos 2 x)dx + c

y(secx) = ∫x 2 .cosxdx + c

y(secx) = x 2 ∫cosxdx – ∫{(d/dx)x 2 ∫cosxdx}dx + c

y(secx) = x 2 senx – 2∫xsenxdx + c

y(secx) = x 2 senx – 2x∫senxdx + 2∫{(dx/dx)∫senxdx}dx + c

y(secx) = x 2 senx + 2xcosx – 2∫cosxdx + c

y(secx) = x 2 senx + 2xcosx – 2senx + c

Esta es la solución requerida.

Pregunta 20. (1 + x 2 )(dy/dx) + y = e^{tan^{-1}x}

Solución:

Tenemos,

(1 + x 2 )(dy/dx) + y = e^{tan^{-1}x}

(dy/dx) + [1/(x 2 + 1)]y =  e^{tan^{-1}x}/(x 2 + 1) ………..(i)

La ecuación dada es una ecuación diferencial lineal de la forma

(dy/dx) + Py = Q

Donde, P = 1/(x 2 + 1), Q =  e^{tan^{-1}x}/(x 2 + 1)

Asi que,

SI = e ∫Pdx

=e^{∫\frac{1}{x^2+1}dx}

= e^{tan^{-1}x}

La solución de una ecuación diferencial es,

y(SI) = ∫Q(SI)dx + c

y( e^{tan^{-1}x}) – ∫[ e^{tan^{-1}x}/(x 2 + 1)] e^{tan^{-1}x}dx + c

Sea, tan -1 x = z

Al diferenciar ambos lados obtenemos

dx/(1 + x 2 ) = dz

ye z = ∫e 2z dz + c

ye z = (e 2z /2) + c

y = (e z /z) + ce -z

y = (1/2) e^{tan^{-1}x} + c.e^{tan^{-1}x}

Esta es la solución requerida.

Pregunta 21. xdy = (2y + 2x 4 + x 2 )dx

Solución:

Tenemos,

xdy = (2y + 2x 4 + x 2 )dx

(dy/dx) = 2(y/x) + 2x 3 + x

(dy/dx) – (y/x) = 2x 3 + x ………..(i)

La ecuación dada es una ecuación diferencial lineal de la forma

(dy/dx) + Py = Q

Donde, P = -(2/x), Q = 2x 3 + x

Asi que,

SI = e ∫Pdx

= e -2∫(dx/x)

= e -2log(x)

= e 2log|1/x|

= 1/ x2

La solución de una ecuación diferencial es,

y(SI) = ∫Q(SI)dx + c

y(1/x 2 ) = ∫(1/x 2 ).(2x 3 + x)dx + c

(y/x 2 ) = ∫[2x + (1/x)]dx + c

(y/x 2 ) = x 2 + log|x| +c

y = x 4 + x 2 log|x| + CX 2

Esta es la solución requerida.

Pregunta 22. (1 + y 2 ) + (x – 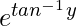 e^{tan^{-1}y})(dy/dx) = 0

Solución:

Tenemos,

(1 + y 2 ) + (x –  e^{tan^{-1}y})(dy/dx) = 0

\frac{dy}{dx}=-\frac{1+y^2}{x-e^{tan^{-1}}x}

\frac{dx}{dy}=-\frac{x-e^{tan^{-1}}x}{1+y^2}

(dx/dy) + x/(1 + y 2 ) =  e^{tan^{-1}y}/(1 + y 2 ) ………..(i)

La ecuación dada es una ecuación diferencial lineal de la forma

(dx/dy) + Px = Q

Donde, P = 1/(1 + y 2 ), Q =  e^{tan^{-1}y}/(1 + y 2 )

Asi que,

SI = e ∫Pdy

e^{∫\frac{dy}{1+y^2}}

= e^{tan^{-1}y}

La solución de una ecuación diferencial es,

x(SI) = ∫Q(SI)dy + c

x(e^{tan^{-1}y})=∫(e^{tan^{-1}y})(\frac{e^{tan^{-1}y}}{1+y^2})dy+c

Sea, tan -1 y = z

Al diferenciar ambos lados tenemos,

dy/(1 + y 2 ) = dz

xe z = ∫e 2z dz + c

xez = (e2z/2) + c

x = e z /2 + ce -z

x=\frac{e^{tan^{-1}y}}{2}+c.e^{tan^{-1}y}

Esta es la solución requerida.

Pregunta 23. y 2 (dx/dy) + x – 1/y = 0

Solución:

Tenemos,

y 2 (dx/dy) + x – 1/y = 0

(dx/dy) + (x/y 2 ) = 1/y 3    ………..(i)

La ecuación dada es una ecuación diferencial lineal de la forma

(dx/dy) + Px = Q

Donde, P = 1/año 2 , Q = 1/año 3

Asi que,

SI = e ∫Pdy

= e ∫dy/y2

= e -(1/año)

La solución de una ecuación diferencial es,

x(SI) = ∫Q(SI)dy + c

e -(1/y) x = ∫(1/y 3 ).(e -1/y )dy + c

Sea,-(1/y) = z

Diferenciando ambos lados tenemos,

(dy/y 2 ) = dz 

xe z = -∫ze z dz + c

xe z = -z∫e z dz + ∫{(dz/dz)∫e z dz}dz + c

xe z = -ze z + ∫e z dz + c

xe z = -ze z + e z + c

x = (1 – z) + ce – z

x = [1 + (1/año)] + ce 1/año

x = (y + 1)/y + ce 1/y

Esta es la solución requerida.

Publicación traducida automáticamente

Artículo escrito por vivekray59 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *