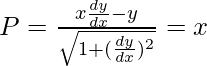Pregunta 23. En cada punto de una curva, la pendiente es la suma de la abscisa y el producto de la ordenada y la abscisa, y la curva pasa por (0, 1) Encuentra la ecuación de la curva.
Solución:
La pendiente viene dada por, (dy/dx)
Tenemos,
(dy/dx) = x + xy
(dy/dx) = x(y + 1)
dy/(y + 1) = xdx
Al integrar ambos lados, obtenemos
∫dy/(y + 1) = ∫xdx
Log|y + 1| = (x 2 /2) + c …(yo)
Como la curva pasa por (0, 1)
Registro|2| = do
Log|y + 1| = (x 2 /2) + Log|2|
Registro|(y + 1)/2| =x2 / 2
Pregunta 24. Una curva es tal que la longitud de la perpendicular desde el origen en la tangente en cualquier punto de la curva es igual a la abscisa de P. Demuestre que la ecuación diferencial de la curva es y 2 – 2xy(dy/dx) – x 2 = 0 y, por lo tanto, encuentre la curva.
Solución:
La tangente de la curva está dada por,
Y – y = (dy/dx)(X – x)
Si P es perpendicular al origen, entonces
x 2 (dy/dx) 2 – 2xy(dy/dx) + y 2 = x 2 + x 2 (dy/dx) 2
y 2 – 2xy(dy/dx) – x 2 = 0
Por lo tanto Probado.
Ahora encontramos la curva.
Entonces, tenemos y 2 – 2xy(dy/dx) – x 2 = 0
(dy/dx) = (y 2 – x 2 )/2xy
La ecuación anterior es una ecuación homogénea.
Sea, y = vx
Al diferenciar ambos lados tenemos,
(dy/dx) = v + x(dv/dx)
v + x(dv/dx) = (v 2 x 2 – x2)/2xvx
v + x(dv/dx) = (v 2 – 1)/2v
x(dv/dx) = [(v 2 – 1)/2v] – v
x(dv/dx) = (v 2 – 1 – 2v 2 )/2v
x(dv/dx) = -(1 + v2 ) /2v
2vdv/(1 + v 2 ) = -(dx/x)
Sobre la integración de ambos lados
∫2vdv/(1 + v 2 ) = -∫(dx/x)
registro|1 + v 2 | = -log|x| + log|c|
log|x(1 + v 2 )| = registro|c|
x(1 + y 2 /x 2 ) = c
(x2 + y2 ) = cx
Pregunta 25. Encuentra la ecuación de la curva que pasa por el punto (1, 2) y la distancia entre el pie de la ordenada del punto de contacto y el punto de intersección de la tangente con el eje x es el doble de la abscisa de el punto de contacto.
Solución:
Consideremos
el punto de contacto de la tangente = P(x, y)
y la curva es y = f(x).
La ecuación de la tangente de la curva está dada por,
Y – y = (dy/dx)(X – x)
Donde (X, Y) es un punto arbitrario en la tangente.
Poniendo Y = 0,
0 – y = (dy/dx)(X – x)
(X – x) = -y(dx/dy)
X = x – y(dx/dy)
Coordenadas en el contacto del eje x = [x – y(dx/dy), 0]
La distancia entre el pie de la ordenada del punto de
contacto y el punto de intersección de la tangente con el eje x es igual a 2x.
y(dx/dy) = 2x
(dx/x) = 2(dy/y)
Sobre la integración de ambos lados
∫(dx/x) = 2∫(dy/y)
registro|x| = 2log|y| + log|c| …(i)
La curva está pasando por (1, 2)
registro|1| = 2log|2| + log|c|
registro|c| = -2log|2|
Al poner el valor de log|c| en la ecuación (i)
registro|x| = 2log|y| – 2log|2|
registro|x| = log|y 2 /4|
x = (y2 / 4)
y2 = 4x
Pregunta 26. La normal a una curva dada en cada punto es (x, y) en la curva que pasa por el punto (3, 0). Si la curva contiene el punto (3, 4). Encuentra su ecuación.
Solución:
Consideremos el punto de la curva = P(x, y).
La ecuación de la tangente de la curva está dada por,
Y – y = -(dx/dy)(X – x) …(i)
Pasa por (3, 0) Entonces,
0 – y = -(dx/día)(3 – x)
ydy = 3dx – xdx
Sobre la integración de ambos lados
∫ydy = 3∫dx – ∫xdx
(y2 / 2 ) = 3x – (x2 / 2 ) + c
Pasa por (3, 4)
(16/2) = 9 – (9/2) + c …(ii)
c = (16/2) – (9/2)
c = (7/2)
(y2 / 2 ) = 3x – (x2 / 2 ) + (7/2)
o
y2 = 6x – x2 + 7
Pregunta 27. La tasa de aumento de bacterias en cultivo es proporcional al número de bacterias presentes, y se encuentra que el número se duplica en 6 horas. Demostrar que la bacteria se vuelve 8 veces al cabo de 18 horas.
Solución:
Consideremos
el recuento inicial de bacterias = P 0
el recuento de bacterias en un momento determinado ‘t’ = P
y el crecimiento de bacterias = g veces.
Tenemos,
dP/dt ∝ P
dP/dt = gP
dP/P = gdt
Sobre la integración de ambos lados
∫(dP/P) = g∫dt
Registro|P| = gt + c
En t = 0, P = P 0
registro|P 0 | = do
Registro|P| = gt + log|P 0 |
Registro|P/P 0 | = gt
El recuento de bacterias se duplica en 6 horas.
En t = 6, P = 2P 0
Registro|2P 0 /P 0 | = 6g
g = logaritmo|2|/6
Registro|P/P 0 | = [Logaritmo|2|/6] × t
Después de t = 18 horas, el recuento de bacterias es igual a
Registro|P/P 0 | = [Logaritmo|2|/6] × 18
Registro|P/P 0 | = 3Registro|2|
Registro|P/P0| = Registro|2| 3
(P/P 0 ) = 8
P = 8P 0
Por lo tanto probado
Pregunta 28. El radio se descompone a una velocidad proporcional a la cantidad de radio presente. Se comprueba que en 25 años se ha descompuesto aproximadamente el 1,1% de una determinada cantidad de radio. Determine aproximadamente cuánto tiempo tardará en descomponerse la mitad de la cantidad original de radio.
Solución:
Consideremos
la cantidad original de radio = P 0
y la cantidad de radio en un momento particular ‘t’ = P
Tenemos,
dP/dt ∝ P
(dP/dt) = -kP (Donde k es constante proporcional)
(dP/P) = -kdt
Sobre la integración de ambos lados
∫(dP/P) = -∫kdt
Registro|P| = -kt + c …(i)
En t = 0, P = P 0
Registro|P 0 | = 0 + c
c = registro|P 0 |
Registro|P| = -kt + Log|P 0 |
Registro|P/P 0 | = -kt …(ii)
Según la pregunta,
En 25 años las bacterias se descomponen un 1,1%.
Entonces, P = (100 – 1.1)% P 0
P = 0.989P 0
Registro|P/P 0 | = -kt
Registro|0.989| = -25k
k = -(1/25)Logaritmo|0,989|
Al poner el valor de k en la ecuación (ii)
Registro|P/P 0 | = (1/25)Logaritmo|0,989| × t
Tiempo ‘T’ para la mitad de la cantidad original de radio (es decir, P 0 = P/2)
Registro|P 0 /(P 0 /2)| = (1/25)Logaritmo|0,989| × t
Registro|2| = (1/25)Logaritmo|0,989| × t
t = (25Log|2|/Log|0,989|)
t = (25 × 0,69311)/(0,01106)
t = 1566,70
t = 1567 años
Pregunta 29. Muestre que todas las curvas cuya pendiente en cualquier punto (x, y) es (x 2 + y 2 )/2xy son hipérbolas rectangulares.
Solución:
Tenemos,
(dy/dx) = (x2 + y2 )/ 2xy
La ecuación dada es una ecuación homogénea,
Entonces, consideremos, y = vx
Al diferenciar ambos lados tenemos,
(dy/dx) = v + x(dv/dx)
(dy/dx) = (x 2 + v 2 x 2 )/2xvx
v + x(dv/dx) = (x 2 + v 2 x 2 )/2xvx
v + x(dv/dx) = (1 + v2 ) /2v
x(dv/dx) = [(1 + v 2 )/2v] – v
x(dv/dx) = (1 + v2 – 2v2 ) /2v
x(dv/dx) = (1 – v2 ) /2v
2vdv/(1 – v 2 ) = (dx/x)
Sobre la integración de ambos lados
∫2vdv/(1 – v 2 ) = ∫(dx/x)
-log|1 – v 2 | = registro|x| – registro|c|
-log|(1 – v 2 )| = -[registro|c| – registro|x|]
-log|(1 – v 2 )| = -log|c/x|
(1 – v 2 ) = c/x
(1 – y 2 /x 2 ) = c/x
(x 2 – y 2 )/x 2 = c/x
(x 2 – y 2 ) = cx
Esta es la ecuación requerida de una hipérbola rectangular.
Pregunta 30. La pendiente de la tangente en cada punto de una curva es igual a la suma de las coordenadas del punto. Encuentra la curva que pasa por el origen.
Solución:
La ecuación de la tangente de la curva está dada por,
(dy/dx) = x + y
(dy/dx) – y = x
La ecuación dada es una ecuación diferencial lineal de la forma
(dx/dy) + Px = Q
Donde, P = -1, Q = -x
Entonces, SI = e ∫Pdx
= e ∫-dx
= e- x
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx+c
y(e -x ) = ∫(x).(e -x )dy+c
y(e -x ) = x∫e -x dx-∫{(dx/dx)∫e -x dx}dx+c
y(e -x ) = -xe -x x + ∫e -x + c
y(e -x ) = -xe -x – e -x + c
y(e -x ) = -e -x (x + 1) + c (i)
Ya que la curva pasa por el origen. Asi que,
0 = -e -0 (1) + c
c = 1
Al poner el valor de c en la ecuación (i)
y(e -x ) = -e -x (x + 1) + c
(x + y + 1) = ce x
Pon c = 1
x + y + 1 = e x
Pregunta 31. Hallar la ecuación de la curva que pasa por el punto (0, 1) si la pendiente de la tangente a la corriente en cada uno de sus puntos es igual a la suma de las abscisas y el producto de las abscisas y las ordenadas del punto.
Solución:
La ecuación de la tangente de la curva está dada por
(dy/dx) = x + xy
(dy/dx) – xy = x
La ecuación dada es una ecuación diferencial lineal de la forma
(dx/dy) + Px = Q
Donde, P = -x, Q = x
Entonces, SI = e ∫Pdx
= e -∫xdx
La solución de una ecuación diferencial es,
y(SI) = ∫Q(SI)dx + c
Dejar,
Sea,x 2 /2 = z
Al diferenciar ambos lados,
xdx = dz
yo = ∫e -z dz
yo = -e -z
Asi que,
La curva pasa por el punto (0, 1).
1e 0 = -e 0 + c
c = 2
Pregunta 32. La pendiente de una curva en cada uno de sus puntos es igual al cuadrado de la abscisa del punto. Encuentre la curva particular que pasa por el punto (-1, 1).
Solución:
Según la pregunta,
(dy/dx) = x 2
dy = x 2 dx
Sobre la integración de ambos lados
∫dy = ∫x 2 dx
y = (x 3 /3) + c …(yo)
La curva pasa por el punto (-1, 1)
1 = -(1/3) + do
c = (4/3)
Al poner el valor de c en la ecuación (i)
y = (x3 / 3) + (4/3)
3y = x3 + 4
Pregunta 33. Halla la ecuación de la curva que pasa por el punto (0, a) y como tal en cualquier punto (x, y) de él, el producto de su pendiente por la ordenada es igual a la abscisa.
Solución:
Según la pregunta,
y(dy/dx) = x
dy = x2dx
Sobre la integración de ambos lados
∫ydy = ∫xdx
(y 2 /2) = (x 2 /2) + c …(i)
La curva pasa por el punto (0, a)
(un 2 /2) = c
c = un 2 /2
Al poner el valor de c en la ecuación (i)
(y 2 /2) = (x 2 /2) + (a 2 /2)
x2 – y2 = -a2 _
Pregunta 34. La intersección x de la recta tangente a una curva es igual a la ordenada del punto de contacto. Encuentre la curva particular que pasa por el punto (1, 1).
Solución:
La pendiente en cualquier punto viene dada por P = (dy/dx)
Según la pregunta,
La pendiente en cualquier punto es igual a la ordenada
Tenemos,
(dy/dx) = y
dy/y = dx
Sobre la integración de ambos lados
∫(dy/y) = ∫(dx)
log|y| = x + registro|c|
log|y| = logaritmo|e x | + log|c|
y = ce x …(i)
La curva pasa por el punto (1, 1)
1 = ce
c = e- 1
Al poner el valor de c en la ecuación (i)
y = e x .e -1
y = e (x-1)
Publicación traducida automáticamente
Artículo escrito por vivekray59 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA