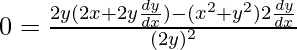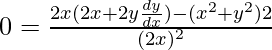Pregunta 1. Forme la ecuación diferencial de la familia de curvas representada por y 2 = (x – c) 3
Solución:
y 2 = (x – c) 3
Al derivar la ecuación dada con x,
2y(dy/dx) = 3(x – c) 2
(x – c) 2 = (2y/3)(dy/dx)
(x – c) = [(2y/3)(dy/dx)] 1/2 -(1)
Al poner el valor de (x – c) en la ecuación (1), obtenemos
y2 = [(2y/3)(dy/dx)] 3/2
Al elevar al cuadrado ambos lados, obtenemos
y 4 = [(2y/3)(dy/dx)] 3
y 4 = (8y 3 /27)(dy/dx) 3
27y 4 = 8y 3 (dy/dx) 3
27y = 8(dy/dx) 3
Pregunta 2. Formar la ecuación diferencial correspondiente a y = e mx eliminando m.
Solución:
y = e mx -(1)
Al derivar la ecuación dada con x,
dy/dx = yo mx -(2)
De la ecuación (1), obtenemos
y = e mx
logía = mx
m = (logía/x)
Ahora, pon el valor de m en la ecuación (2), obtenemos
x(dy/dx) = ylogía
Pregunta 3. Forme las ecuaciones diferenciales a partir de las siguientes primitivas donde las constantes son arbitrarias.
(i) y2 = 4ax
Solución:
y 2 = 4ax -(1)
y 2 /4x = a
Al derivar la ecuación dada con x,
2y(dy/dx) = 4a -(2)
Ahora, pon el valor de a en la ecuación (2), obtenemos
2y(dy/dx) = 4(y 2 /4x)
2y(dy/dx) = y 2 /x
2x(dy/dx) = y
(ii) y = cx + 2c 2 + c 3
Solución:
y = cx + 2c 2 + c 3 -(1)
Al derivar la ecuación dada con x,
dy/dx = c -(2)
Ahora, pon el valor de c en la ecuación (1), obtenemos
y = x(dy/dx) + 2(dy/dx) 2 + (dy/dx) 3
(iii) xy = a 2
Solución:
xy = a 2 -(1)
Al derivar la ecuación dada con x,
x(dy/dx) + y = 0
(iv) y = ax2 + bx + c
Solución:
y = ax 2 + bx + c -(1)
Al derivar la ecuación dada con x,
dy/dx = 2ax + b -(2)
Nuevamente derivando la ecuación dada con x,
d 2 y/dx 2 = 2a -(3)
Nuevamente, derivando la ecuación dada con x, obtenemos
d 3 y/dx 3 = 0
Pregunta 4. Encuentra la ecuación diferencial de la familia de curvas y = Ae 2x + Be -2x donde A y B son constantes arbitrarias.
Solución:
y = Ae 2x + Be -2x -(1)
Al derivar la ecuación dada con x,
(dy/dx) = 2Ae 2x – 2Be -2x -(2)
De nuevo, derivando la ecuación dada con x,
d 2 y/dx 2 = 4Ae 2x + 4Be -2x
d 2 y/dx 2 = 4(Ae 2x + Be -2x )
d 2 y/dx 2 = 4y
Pregunta 5. Encuentra la ecuación diferencial de la familia de curvas, x = Aconst + Bsinnt donde A y B son constantes arbitrarias.
Solución:
x = Acosnt + Bsennt -(1)
Al derivar la ecuación dada con x,
dy/dx = -Ansinnt + Bncosnt -(2)
De nuevo, derivando la ecuación dada con x,
d 2 y/dx 2 = -An 2 costo – Bn 2 sinto
d 2 y/dx 2 = -n 2 (Acosnt + Bsennt)
re 2 y/dx 2 + norte 2 x = 0
Pregunta 6. Forme la ecuación diferencial correspondiente a y 2 = a(b – x 2 ) eliminando a y b.
Solución:
y2 = a(b – x2 )
Al derivar la ecuación dada con x,
2y(dy/dx) = a(0 – 2x)
De nuevo, derivando la ecuación dada con x,
X[
Pregunta 7. Forme la ecuación diferencial correspondiente a y 2 – 2ay + x 2 = a 2 eliminando a.
Solución:
y 2 – 2ay + x 2 = a 2 -(1)
Al derivar la ecuación dada con x,
2y(dy/dx) – 2a(dy/dx) + 2x = 0
2y(dy/dx) + 2x = 2a(dy/dx)
-(2)
Consideremos dy/dx = y’
Al poner el valor de ‘a’ en la ecuación (1), obtenemos
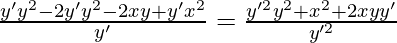
Al resolver esta ecuación, obtenemos
(x 2 – 2y 2 )y’ 2 – 4xyy’ – x 2 = 0
(x 2 – 2y 2 )(dy/dx) 2 – 4xy(dy/dx) – x 2 = 0
Pregunta 8. Forme la ecuación diferencial correspondiente a (x – a) 2 + (y – b) 2 = r 2 eliminando a y b.
Solución:
(x – a) 2 + (y – b) 2 = r 2 -(1)
Al derivar la ecuación dada con x,
2(x – a) + 2(y – b)(dy/dx) = 0
(x – a) + (y – b)(dy/dx) = 0 -(2)
De nuevo, derivando la ecuación dada con x,
1 + (y – b)(d 2 y/dx 2 ) + (dy/dx)(dy/dx) = 0
-(3)
Al poner el valor de (y – b) en la ecuación (2),
(x – a)(d 2 y/dx 2 ) – (dy/dx) 3 – (dy/dx) = 0
-(4)
Al poner el valor de (x – a) y (y – b) en la ecuación (1)
Ponga (dy/dx) = y’ y d 2 y/dx 2 = y”
y’ 2 (1 + y’ 2 ) 2 + (1 + y’ 2 ) 2 = r 2 y” 2
Pregunta 9. Encuentra la ecuación diferencial de todos los círculos que pasan por el origen y cuyos centros se encuentran en el eje.
Solución:
La ecuación del círculo es (x – a) 2 + (y – b) 2 = r 2
Aquí, a y b son el centro del círculo.
(x – a) 2 + (y – b) 2 = r 2 -(1)
Cuando el centro se encuentra en el eje y, entonces a = 0
x 2 + (y – b) 2 = r 2 -(2)
Entonces, cuando el círculo pasa por el origen, entonces la ecuación es
0 2 + segundo 2 = r 2 -(3)
x 2 + (y – b) 2 = r 2
Al elevar al cuadrado ambos lados, tenemos
x 2 + y 2 – 2 años + r 2 = r 2 -(Puesto que r 2 = b 2 )
2 años = x 2 + y 2
r = (x2 + y2 )( 2y )
Al diferenciar la ecuación (1) con x, obtenemos
0 = 4xy + 4y 2 (dy/dx) – 2x 2 (dy/dx) – 2y 2 (dy/dx)
0 = y 2 (dy/dx) – x 2 (dy/dx) + 2xy
(x 2 – y 2 )(dy/dx) = 2xy
Pregunta 10. Encuentra la ecuación diferencial de todos los círculos que pasan por el origen y cuyos centros se encuentran en el eje x.
Solución:
La ecuación del círculo es (x – a) 2 + (y – b) 2 = r 2
Aquí, a y b son el centro del círculo.
Cuando el centro se encuentra en el eje x, entonces b = 0
(x – a) 2 + y 2 = r 2 -(1)
Cuando el círculo pasa por el origen, entonces la ecuación es
un 2 + 0 2 = r 2 -(2)
(x – a) 2 + y 2 = r 2
Al elevar al cuadrado ambos lados, obtenemos,
x 2 – 2ax + a 2 + y 2 = r 2
x 2 + y 2 – 2xr + r 2 = r 2 -(Puesto que r 2 = a 2 )
2xr = x2 + y2
r = (x 2 + y 2 )(2x) -(3)
Al diferenciar la ecuación con x, obtenemos
0 = 2x 2 + 2xy(dy/dx) – x 2 – y 2
(x2 – y2 ) + 2xy(dy/dx) = 0
Publicación traducida automáticamente
Artículo escrito por vivekray59 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
![Rendered by QuickLaTeX.com y^2-2[\frac{y\frac{dy}{dx}+x}{\frac{dy}{dx}}]y+x^2=[\frac{y\frac{dy}{dx}+x}{\frac{dy}{dx}}]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-06c8c3b3b7d7f144e3c425a9e67bbce8_l3.png)
![Rendered by QuickLaTeX.com (x-a)-[\frac{(\frac{dy}{dx})^2+1}{\frac{d^2y}{dx^2}}]\frac{dy}{dx}=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5388ca8e8337369b849f6ab0e2c6fdb6_l3.png)
![Rendered by QuickLaTeX.com [\frac{(\frac{dy}{dx})^3+(\frac{dy}{dx})}{(\frac{d^2y}{dx^2})}]^2+ [\frac{(\frac{dy}{dx})^2+1}{\frac{d^2y}{dx^2}}]^2=r^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-229a46abad08a4e8243a8cce5155f2f9_l3.png)