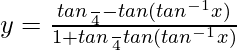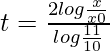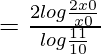Clase 12 Soluciones RD Sharma – Capítulo 22 Ecuaciones Diferenciales – Ejercicio 22.7| conjunto 3

Resuelva las ecuaciones diferenciales (pregunta 40-48):

Pregunta 40. 2x(dy/dx) = 3y, y(1) = 2

Solución:

Tenemos,

2x(dy/dx) = 3y

2dy/y = 3dx/x

Al integrar ambos lados,

2∫dy/y = 3∫dx/x

2log(y) = 3log(x) + log(c)

y ² = x ³ c

Ponga x = 1, y = 2 en la ecuación anterior

c = 4

y ² = 4x ³

Pregunta 41. xy(dy/dx) = y + 2, y(2) = 0

Solución:

Tenemos,

xy(dy/dx) = y + 2

ydy/(y + 2) = dx/x

Al integrar ambos lados,

∫ydy/(y + 2) = ∫(dx/x)

∫1 – \frac{2}{(y+2)} dy = ∫(dx/x)

y – 2log(y + 2) = log(x) + log(c)

Ponga x = 2, y = 0 en la ecuación anterior

0 – 2log(2) = log(2) + log(c)

registro (c) = -3 registro (2)

registro (c) = registro (1/8)

c = (1/8)

y – 2log(y + 2) = log(x/8)

Pregunta 42. (dy/dx) = 2e ^x y ³ , y(0) = 1/2

Solución:

Tenemos,

(dy/dx) = 2e ^x y ³

dy/y ³ = 2e ^x dx

Al integrar ambos lados,

∫dy/y ³ = 2∫e ^x dx

-(1/2y ² ) = 2e ^x + c

Ponga x = 0, y = (1/2) en la ecuación anterior

-(4/2) = 2 + c

c = -4

-(1/2y ² ) = 2e ^x – 4

y ² (4e ^x – 8) = -1

y ² (8 – 4e ^x ) = 1

Pregunta 43. (dr/dt) = -rt, r(0) = r ₀

Solución:

Tenemos,

(dr/dt) = -rt

dr/r = -tdt

Al integrar ambos lados,

∫dr/r = -∫tdt

log(r) = -t ² /2 + c

Ponga t = 0, r =r ₀ en la ecuación anterior

c = registro (r ₀ )

registro (r) = -t2/2 + registro (r ₀ )

log(r/r ₀ ) = -t ² /2

(r/r0 ₎ = $e^{-\frac{t^2}{2}}$

r = r ₀ $e^{-\frac{t^2}{2}}$

Pregunta 44. (dy/dx) = ysen2x, y(0) = 1

Solución:

Tenemos,

(dy/dx) = ysen2x

dy/y = sen2xdx

Al integrar ambos lados,

∫(dy/y) = ∫sen2xdx

log(y) = -(1/2)cos2x + c

Ponga x = 0, y = 1 en la ecuación anterior

registro|1| = -cos0/2 + c

c = (1/2)

log(y) = (1/2) – (cos2x/2)

log(y) = (1 – cos2x)/2

log(y) = 2sen 2x / ²

log(y) = sen ² x

y = $e^{sin^2x}$

Pregunta 45(i). (dy/dx) = ytanx, y(0) = 1

Solución:

Tenemos,

(dy/dx) = ytanx

(dy/y) = tanxdx

Sobre la integración de ambos lados

∫(dy/y) = ∫tanxdx

log(y) = log(segx) + c

Ponga x = 0, y = 1 en la ecuación anterior

0 = registro (1) + c

c = 0

log(y) = log(segx)

y = secx

Pregunta 45(ii). 2x(dy/dx) = 5y, y(1) = 1

Solución:

Tenemos,

2x(dy/dx) = 5y

(2dy/y) = 5dx/x

Sobre la integración de ambos lados

2∫(dy/y) = 5∫(dx/x)

2log(y) = 5log(x) + c

Ponga x = 1, y = 1 en la ecuación anterior

2log(1) = 5log(1) + c

c = 0

2log(y) = 5log(x)

y ² = x ⁵

y = |x| ^(5/2)

Pregunta 45(iii). (dy/dx) = 2e ^2x y ² , y(0) = -1

Solución:

Tenemos,

(dy/dx) = 2e ^2x y ²

(dy/y2) = 2e ^2x dx

Sobre la integración de ambos lados

∫(dy/y ² ) = 2∫e ^2x dx

-(1/y) = 2e ^2x /2 + c

-(1/y) = e ^2x + c

Ponga x = 0, y = -1 en la ecuación anterior

1 = mi ⁰ + c

c = 0

-(1/y) = e ^2x

y = -e ^-2x

Pregunta 45(iv). acogedor(dy/dx) = e ^x , y(0) = π/2

Solución:

Tenemos,

acogedor(dy/dx) = e ^x

acogedor = e ^x dx

Sobre la integración de ambos lados

∫cosydy = ∫e ^x dx

seno = e ^x + c

Ponga x = 1, y = π/2 en la ecuación anterior

sen(π/2) = mi ⁰ + c

1 = 1 + c

c = 0

seno = e ^x

y = sen ^-1 (e ^x )

Pregunta 45(v). (dy/dx) = 2xy, y(0) = 1

Solución:

Tenemos,

(dy/dx) = 2xy

dy/y = 2xdx

Sobre la integración de ambos lados

∫(dy/y) = 2∫xdx

registro (y) = x ² + c

Ponga x = 0, y = 1 en la ecuación anterior

registro (1) = 0 + c

c = 0

registro (y) = x ²

Pregunta 45 (vi). (dy/dx) = 1 + x ² + y ² + x ² y ² , y(0) = 1

Solución:

Tenemos,

(dy/dx) = 1 + x ² + y ² + x ² y ²

(dy/dx) = (1 + x ² ) + y ² (1 + x ² )

(dy/dx) = (1 + x ² )(1 + y ² )

$\frac{dy}{(1+y^2)}=(1+x^2)dx$

Sobre la integración de ambos lados

$∫\frac{dy}{(1+y^2)}=∫(1+x^2)dx$

bronceado ^-1 y = x + (x ³ /3) + c

Ponga x = 0, y = 1 en la ecuación anterior

bronceado ^-1 (1) = 0 + 0 + c

c = π/4

bronceado ^-1 y = x + (x ³ /3) + π/4

Pregunta 45 (vii). xy(dy/dx) = (x + 2)(y + 2), y(1) = -1

Solución:

Tenemos,

xy(dy/dx) = (x + 2)(y + 2)

ydy/(y + 2) = (x + 2)dx/x

Sobre la integración de ambos lados

∫ydy/(y + 2) = ∫(x + 2)dx/x

∫[1 – 2/(y + 2)]dy = ∫dx + 2∫(dx/x)

y – 2log(y + 2) = x + 2log(x) + c

Ponga x = 1, y = -1 en la ecuación anterior

-1 – 2log(-1 + 2) = 1 + 2log(1) + c

c = -2

y – 2log(y + 2) = x + 2log(x) – 2

Pregunta 45 (viii). (dy/dx) = 1 + x + y ² + xy ² , y(0) = 0

Solución:

Tenemos,

(dy/dx) = 1 + x + y ² + xy ²

(dy/dx) = (1 + x) + y ² (1 + x)

(dy/dx) = (1 + x)(1 + y ² )

Sobre la integración de ambos lados

$∫\frac{dy}{(1+y^2)}=∫(1+x)dx$

bronceado ^-1 (y) = x + (x ² /2) + c

Ponga x = 0, y = 0 en la ecuación anterior

bronceado ^-1 (0) = 0 + 0 + c

c = 0

bronceado ^-1 (y) = x + (x ² /2)

y = tan(x + x ² /2)

Pregunta 45(ix). 2(y + 3) – xy(dy/dx) = 0, y(1) = -2

Solución:

Tenemos,

2(y + 3) – xy(dy/dx) = 0

xy(dy/dx) = 2(y + 3)

ydy/(y + 3) = 2(dx/x)

Sobre la integración de ambos lados

∫[ydy/(y + 3)] = 2∫(dx/x)

∫[1 – 3/(y + 3)]dy = 2∫(dx/x)

y – 3log(y + 3) = 2log(x) + c

Ponga x = 1, y = -2 en la ecuación anterior

-2 – 3log(-2 + 3) = 2log(1) + c

c = -2

y – 3log(y + 3) = 2log(x) – 2

y + 2 = logaritmo(x) ² logaritmo(y + 3) ³

e ^(y+2) = x ² (y + 3) ³

Pregunta 46. x(dy/dx) + coty = 0, y = π/4 en x = √2

Solución:

Tenemos,

x(dy/dx) + coty = 0

x(dy/dx) = -coty

dy/coti = -dx/x

Sobre la integración de ambos lados

∫dy/coti = -∫dx/x

∫tanydy = -∫(dx/x)

log(seguridad) = -log(x) + c

log(xsecy) = c

Ponga x = √2, y = π/4 en la ecuación anterior

registro|√2.√2| = do

c = registro (2)

log(xsecy) = log(2)

x/acogedor = 2

x = 2acogedor

Pregunta 47. (1 + x ² )(dy/dx) + (1 + y ² ) = 0, y = 1 en x = 0

Solución:

Tenemos,

(1 + x ² )(dy/dx) + (1 + y ² ) = 0

(1 + x ² )(dy/dx) = -(1 + y ² )

$\frac{dy}{(1+y^2)}=\frac{-dx}{(1+x^2)}$

Sobre la integración de ambos lados

$∫\frac{dy}{(1+y^2)}=-∫\frac{dx}{(1+x^2)}$

tan ^-1 y = -tan ^-1 x + c

Ponga x = 0, y = 1 en la ecuación anterior

bronceado ^-1 (1) = bronceado ^-1 (0) + c

c = π/4

bronceado ^-1 y = π/4 – bronceado ^-1 x

y = tan(π/4 – tan ^-1 x)

$y=\frac{tan\frac{π}{4}-tan(tan^{-1}x)}{1+tan\frac{π}{4}tan(tan^{-1}x)}$

y = (1 – x)/(1 + x)

y + yx = 1 – x

x + y = 1 – xy

Pregunta 48. (dy/dx) = 2x(logx + 1)/(seny + ycosy), y = 0 en x = 1

Solución:

Tenemos,

(dy/dx) = 2x(logx + 1)/(seny + ycosy)

(seny + ycosy)dy = 2x(logx + 1)dx

Sobre la integración de ambos lados

∫sinydy + ∫ycosydy = 2∫xlogxdx + 2∫xdx

-cosy + y∫cosydy – ∫[(dy/dy)∫cosydy]dy = 2logx∫xdx – 2∫[( $\frac{d(logx)}{dx}$ ∫xdx]dx + x ² + c

-cosy + yseny – ∫sinydy = x ² logx – ∫xdx + x ² + c

-acogedor + ysiny + acogedor = x ² logx – x ² /2 + x ² + c

Ponga x = 1, y = 0 en la ecuación anterior

-1 + 0 + 1 = 0 – (1/2) + 1 + c

do = -(1/2)

yseno = x ² logx + x ² /2 – (1/2)

2yseny = 2x ² logx + x ² – 1

Pregunta 49. Hallar la solución particular de la ecuación diferencial e ^(dy/dx) = x + 1, dado que y(0) = 3 cuando x = 0.

Solución:

Tenemos,

e ^(dy/dx) = x + 1

Tomando registro de ambos lados,

(dy/dx) = log(x + 1)

dy = log(x + 1)dx

Sobre la integración de ambos lados

∫dy = ∫log(x + 1)dx

y = log(x + 1)∫dx – ∫[ $\frac{d(log(x+1))}{dx}$ ∫dx]dx

y = xlog(x + 1) – ∫xdx/(x + 1)

y = xlog(x + 1) – ∫[1 – 1/(x + 1)]dx

y = xlog(x + 1) – x + log(x + 1) + c

y = (x + 1)log(x + 1) – x + c

Ponga x = 0, y = 3 en la ecuación anterior

3 = 0 – 0 + c

c = 3

y = (x + 1)log(x + 1) – x + 3

Pregunta 50. Hallar la solución de la ecuación diferencial cosydy + cosxsinydx = 0, dado que y = π/2 cuando x = π/2.

Solución:

Tenemos,

cosydy + cosxsinydx = 0

cosydy = -cosxsinydx

(acogedor/sencillo)dy = -cosxdx

Sobre la integración de ambos lados

∫cotydy = -∫cosxdx

log(seno) = -senx + c

Ponga x = π/2, y = π/2 en la ecuación anterior

log|senπ/2| = -sen(π/2) + c

0 = -1 + c

c = 1

log(seno) = 1 – sen(x)

log(seno) + sen(x) = 1

Pregunta 51. Hallar la solución particular de la ecuación diferencial (dy/dx) = -4xy ² , dado que y =1 cuando x = 0.

Solución:

Tenemos,

(dy/dx) = -4xy ²

(dy/y ² ) + 4xdx = 0

Sobre la integración de ambos lados

∫(dy/y ² ) + 4∫xdx = 0

-(1/año) + 2x ² = c

Ponga x = 0, y = 1 en la ecuación anterior

-1 + 0 = do

c = -1

-(1/año) + 2x ² = -1

(1/año) = 2x ² + 1

y = 1/(2×2 + 1 ⁾

Pregunta 52. Hallar la ecuación de una curva que pasa por el punto (0, 0) y cuya ecuación diferencial es (dy/dx) = e ^x senx.

Solución:

Tenemos,

(dy/dx) = e ^x senx

dy = e ^x senxdx

Sobre la integración de ambos lados

∫dy = ∫e ^x senxdx

Sea, I = ∫e ^x senxdx

yo = e ^x ∫senx – ∫[ $\frac{de^x}{dx}$ ∫senxdx]dx

yo = -e ^x cosx + ∫e ^x cosxdx

yo = -e ^x cosx + e ^x ∫cosxdx – ∫[ $\frac{de^x}{dx}$ ∫cosxdx]dx

I = -e ^x cosx + e ^x senx – ∫e ^x senxdx

yo = -e ^x cosx + e ^x senx – yo

2I = -e ^x cosx + e ^x senx

I = e ^x (senx – cosx)/2

y = e ^x (senx – cosx)/2

Pregunta 53. Para la ecuación diferencial xy(dy/dx) = (x + 2)(y + 2), encuentre la curva solución que pasa por el punto (1, -1).

Solución:

Tenemos,

xy(dy/dx) = (x + 2)(y + 2)

ydy/(y + 2) = (x + 2)dx/x

Sobre la integración de ambos lados

∫ydy/(y + 2) = ∫(x + 2)dx/x

∫[1 – 2/(y + 2)]dy = ∫dx + 2∫(dx/x)

y – 2log(y + 2) = x + 2log(x) + c

y – x – c = log(x) ² + log(y + 2) ²

y – x – c = log|x ² (y + 2) ² |

La curva está pasando por (1, -1)

-1 – 1 – c = registro (1)

c = 2

y – x – 2 = log|x ² (y + 2) ² |

Pregunta 54. El volumen de un globo esférico que se infla cambia a un ritmo constante. Si inicialmente su radio es de 3 unidades y después de 3 segundos es de 6 unidades. Encuentra el radio del globo después de t segundos.

Solución:

Tenemos,

Sea v el volumen de la esfera, t el tiempo, r el radio de la esfera & k es una constante

El volumen de la esfera viene dado por v = (4/3)πr ³

Según la pregunta (dv/dt) = k

$\frac{d[(4/3)πr^3]}{dt} = k$

(4/3)π.3r ² (dr/dt) = k

4πr ² dr = kdt

Sobre la integración de ambos lados

∫4πr ² dr = ∫kdt

4π(r ³ /3) = kt + c

4πr ³ = 3(kt + c) -(i)

En t = 0, r = 38

4π(3) ³ = 3(0 + c)

c = 36π

En t = 3, r = 6 en la ecuación (i)

4π(6) ³ = 3(kt + 36π)

864π = 9k + 108π

k = 84π

4πr ³ = 3(84πt + 36π)

^r3 = 63t + 27

r = (63t + 27) ^1/3

El radio del globo después de t segundo es (63t + 27) ^1/3

Pregunta 55. En un banco, el principal aumenta a razón de r % anual. Encuentre el valor de r si Rs 100 se duplica en 10 años (log 2 = 0,6931).

Solución:

Tenemos,

Sean ‘p’ y ‘t’ el principal y el tiempo respectivamente.

Principal aumenta a una tasa de r % por año.

dp/dt = (r/100)p

(dp/p) = (r/100)dt

Sobre la integración de ambos lados

∫(dp/p) = (r/100)∫dt

log(p) = (rt/100) + c -(i)

En t = 0, p = 100

registro (100) = 0 + c

c = log(100) -(ii)

Si t = 10, p = 2 × 100 en la ecuación (i)

registro(200) = (10r/100) + registro(100)

registro (200/100) = (10r/100)

registro(2) = (r/10)

0,6931 = (r/10)

r = 6,931

Pregunta 56. En un banco, el principal aumenta a razón del 5% anual. Se deposita una cantidad de Rs 1000 en este banco, ¿cuánto valdrá después de 10 años (e = 1,648).

Solución:

Tenemos,

Sean ‘p’ y ‘t’ el principal y el tiempo respectivamente.

Aumentos de capital a razón del 5% anual,

(dp/dt) = (5/100)p -(i)

(dp/p) = (1/20)dt

Sobre la integración de ambos lados

∫(dp/p) = (1/20)∫dt

log(p) = (t/20) + c -(ii)

En t = 0, p = 1000

registro (1000) = c

registro (p) = (t/20) + registro (1000)

Poniendo t = 10 en la ecuación en (i)

registro (p/1000) = (10/20)

p = 1000e ^0,5

p = 1000 × 1,648

p = 1648

Pregunta 57. En un cultivo, el recuento de bacterias es 100000. El número aumenta en un 10% en 2 horas. ¿En cuántas horas el conteo llegará a 200000, si la tasa de crecimiento de bacterias es proporcional al número presente?

Solución:

Tenemos,

Deje que el número de bacterias en el tiempo ‘t’ sea ‘x’

La tasa de crecimiento de bacterias es proporcional al número presente

(dx/dt)∝ x -(i)

(dx/dt) = kx (donde ‘k’ es constante proporcional)

(dx/x) = kdt

Sobre la integración de ambos lados

∫(dx/x) = k∫dt

log(x) = kt + c -(ii)

En t = 0, x = x ₀ (x ₀ es el número de bacterias en t = 0)

log(x ₀ ) = 0 + c

c = logaritmo(x ₀ )

Al poner el valor de c en la ecuación (ii)

log(x) = kt + log(x ₀ )

log(x/x ₀ ) = kt -(iii)

El número se incrementa en un 10% en 2 horas.

x = x ₀ (1 + 10/100)

(x/x ₀ ) = (11/10)

Al poner el valor de (x/x ₀ ) & t = 2 en la ecuación (iii)

2 × k = registro (11/10)

k = (1/2)log(11/10)

Por lo tanto, la ecuación (iii) se convierte en

log(x/x ₀ ) = (1/2)log(11/10) × t

$t=\frac{2log\frac{x}{x0}}{log\frac{11}{10}}$

En el momento t ₁ el número de bacterias se convierte en 200000 de 100000 (es decir, x = 2x ₀ )

t ₁ $=\frac{2log\frac{2x0}{x0}}{log\frac{11}{10}}$

t ₁ $=\frac{2log2}{log\frac{11}{10}}$

Pregunta 58. Si y(x) es una solución de la ecuación diferencial $[\frac{(2 + sinx)}{(1+y)}](\frac{dy}{dx})=-cosx$ y y(0) = 1, entonces encuentra el valor de y(π/2).

Solución:

Tenemos,

$[\frac{(2 + sinx)}{(1+y)}](\frac{dy}{dx})=-cosx$ (i)

dy/(1 + y) = -[(cosx)/(2 + senx)]dx

Sobre la integración de ambos lados

∫dy/(1 + y) = -∫[(cosx)/(2 + senx)]dx

log(1 + y) = -log(2 + senx) + log(c)

log(1 + y) + log(2 + senx) = log(c)

(1 + y)(2 + senx) = c

Ponga en x = 0, y = 1

c = (1 + 1)(2 + 0)

c = 4

(1 + y)(2 + senx) = 4

(1 + y) = 4/(2 + s inx)

y = 4/(2 + senx) – 1

Necesitamos encontrar el valor de y(π/2)

y = 4/(2 + senπ/2) – 1

y = (4/3) – 1

y = (1/3)

Publicación traducida automáticamente

Artículo escrito por vivekray59 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Resuelva las ecuaciones diferenciales (pregunta 40-48):

Pregunta 40. 2x(dy/dx) = 3y, y(1) = 2

Pregunta 41. xy(dy/dx) = y + 2, y(2) = 0

Pregunta 42. (dy/dx) = 2e x y 3 , y(0) = 1/2

Pregunta 43. (dr/dt) = -rt, r(0) = r 0

Pregunta 44. (dy/dx) = ysen2x, y(0) = 1

Pregunta 45(i). (dy/dx) = ytanx, y(0) = 1

Pregunta 45(ii). 2x(dy/dx) = 5y, y(1) = 1

Pregunta 45(iii). (dy/dx) = 2e 2x y 2 , y(0) = -1

Pregunta 45(iv). acogedor(dy/dx) = e x , y(0) = π/2

Pregunta 45(v). (dy/dx) = 2xy, y(0) = 1

Pregunta 45 (vi). (dy/dx) = 1 + x 2 + y 2 + x 2 y 2 , y(0) = 1

Pregunta 45 (vii). xy(dy/dx) = (x + 2)(y + 2), y(1) = -1

Pregunta 45 (viii). (dy/dx) = 1 + x + y 2 + xy 2 , y(0) = 0

Pregunta 45(ix). 2(y + 3) – xy(dy/dx) = 0, y(1) = -2

Pregunta 46. x(dy/dx) + coty = 0, y = π/4 en x = √2

Pregunta 47. (1 + x 2 )(dy/dx) + (1 + y 2 ) = 0, y = 1 en x = 0

Pregunta 48. (dy/dx) = 2x(logx + 1)/(seny + ycosy), y = 0 en x = 1

Pregunta 49. Hallar la solución particular de la ecuación diferencial e (dy/dx) = x + 1, dado que y(0) = 3 cuando x = 0.

Pregunta 50. Hallar la solución de la ecuación diferencial cosydy + cosxsinydx = 0, dado que y = π/2 cuando x = π/2.

Pregunta 51. Hallar la solución particular de la ecuación diferencial (dy/dx) = -4xy 2 , dado que y =1 cuando x = 0.

Pregunta 52. Hallar la ecuación de una curva que pasa por el punto (0, 0) y cuya ecuación diferencial es (dy/dx) = e x senx.

Pregunta 53. Para la ecuación diferencial xy(dy/dx) = (x + 2)(y + 2), encuentre la curva solución que pasa por el punto (1, -1).

Pregunta 54. El volumen de un globo esférico que se infla cambia a un ritmo constante. Si inicialmente su radio es de 3 unidades y después de 3 segundos es de 6 unidades. Encuentra el radio del globo después de t segundos.

Pregunta 55. En un banco, el principal aumenta a razón de r % anual. Encuentre el valor de r si Rs 100 se duplica en 10 años (log 2 = 0,6931).

Pregunta 56. En un banco, el principal aumenta a razón del 5% anual. Se deposita una cantidad de Rs 1000 en este banco, ¿cuánto valdrá después de 10 años (e = 1,648).

Pregunta 57. En un cultivo, el recuento de bacterias es 100000. El número aumenta en un 10% en 2 horas. ¿En cuántas horas el conteo llegará a 200000, si la tasa de crecimiento de bacterias es proporcional al número presente?

Pregunta 58. Si y(x) es una solución de la ecuación diferencial y y(0) = 1, entonces encuentra el valor de y(π/2).

Deja una respuesta Cancelar la respuesta

Pregunta 42. (dy/dx) = 2e ^x y ³ , y(0) = 1/2

Pregunta 43. (dr/dt) = -rt, r(0) = r ₀

Pregunta 45(iii). (dy/dx) = 2e ^2x y ² , y(0) = -1

Pregunta 45(iv). acogedor(dy/dx) = e ^x , y(0) = π/2

Pregunta 45 (vi). (dy/dx) = 1 + x ² + y ² + x ² y ² , y(0) = 1

Pregunta 45 (viii). (dy/dx) = 1 + x + y ² + xy ² , y(0) = 0

Pregunta 47. (1 + x ² )(dy/dx) + (1 + y ² ) = 0, y = 1 en x = 0

Pregunta 49. Hallar la solución particular de la ecuación diferencial e ^(dy/dx) = x + 1, dado que y(0) = 3 cuando x = 0.

Pregunta 51. Hallar la solución particular de la ecuación diferencial (dy/dx) = -4xy ² , dado que y =1 cuando x = 0.

Pregunta 52. Hallar la ecuación de una curva que pasa por el punto (0, 0) y cuya ecuación diferencial es (dy/dx) = e ^x senx.

Pregunta 58. Si y(x) es una solución de la ecuación diferencial $[\frac{(2 + sinx)}{(1+y)}](\frac{dy}{dx})=-cosx$ y y(0) = 1, entonces encuentra el valor de y(π/2).