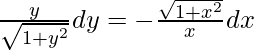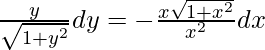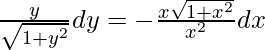Clase 12 Soluciones RD Sharma – Capítulo 22 Ecuaciones diferenciales – Ejercicio 22.7

Resuelve las siguientes ecuaciones diferenciales:

Pregunta 1. (x – 1)(dy/dx) = 2xy

Solución:

Tenemos,

(x – 1)(dy/dx) = 2xy

dy/y = [2x/(x – 1)]dx

Al integrar ambos lados,

∫(dy/y) = ∫[2x + (x – 1)]dx

log(y) = ∫[2 + 2/(x – 1)]dx

log(y) = 2x + 2log(x – 1) + c (Donde ‘c’ es la constante de integración)

Pregunta 2. (x ² + 1)dy = xydx

Solución:

Tenemos,

(x ² + 1)dy = xydx

(dy/y) = [x/(x ² + 1)]dx

Sobre la integración de ambos lados

∫(dy/y) = ∫[x/(x ² + 1)]dx

log(y) = (1/2)∫[2x/(x ² + 1)]dx

log(y) = (1/2)log(x ² + 1) + c (Donde ‘c’ es la constante de integración)

Pregunta 3. (dy/dx) = (e ^x + 1)y

Solución:

Tenemos,

(dy/dx) = (ex ⁺ 1)y

(dy/y) = (ex ⁺ 1)dx

Sobre la integración de ambos lados

∫(dy/y) = ∫(e ^x + 1)dx

log(y) = (e ^x + x) + c (Donde ‘c’ es la constante de integración)

Pregunta 4. (x – 1)(dy/dx) = 2x ³ y

Solución:

Tenemos,

(x – 1)(dy/dx) = 2x ³ y

(dy/y) = [2x ³ /(x – 1)]dx

Sobre la integración de ambos lados

∫(dy/y) = ∫[2x ³ /(x – 1)]dx

∫(dy/y) = 2∫[x ² + x + 1 + 1/(x – 1)]dx

log(y) = (2/3)(x ³ ) + x ² + 2x + 2log(x – 1) + c (Donde ‘c’ es la constante de integración)

Pregunta 5. xy(y + 1)dy = (x ² + 1)dx

Solución:

Tenemos,

xy(y + 1)dy = (x ² + 1)dx

y(y + 1)dy = [(x ² + 1)/x]dx

(y2 ⁺ y)dy = xdx + (dx/x)

Al integrar ambos lados,

∫(y ² + y)dy = ∫xdx + (dx/x)

(y ³ /3) + (y ² /2) = (x ² /2) + log(x) + c (donde ‘c’ es la constante de integración)

Pregunta 6. 5(dy/dx) = e ^x y ⁴

Solución:

Tenemos,

5(dy/dx) = e ^x y ⁴

5(dy/y ⁴ ) = e ^x

Al integrar ambos lados,

5∫(dy/y ⁴ ) = ∫e ^x

-(5/3)(1/y ³ ) = e ^x + c (Donde ‘c’ es la constante de integración)

Pregunta 7. xcosydy = (xe ^x logx + e ^x )dx

Solución:

Tenemos,

xcosydy = (xe ^x logx + e ^x )dx

cosydy = e ^x (logx + 1/x)dx

Al integrar ambos lados,

∫cosydy = ∫e ^x (logx + 1/x)dx

Ya que, ∫[f(x) + f'(x)]e ^x dx] = e ^x f(x)

siny = e ^x logx + c (Donde ‘c’ es la constante de integración)

Pregunta 8. (dy/dx) = e ^x+y + x ² e ^y

Solución:

Tenemos,

(dy/dx) = e ^x+y + x ² e ^y

(dy/dx) = e ^x e ^y + x ² e ^y

dy = e ^y (ex + x ²⁾ dx

e ^-y dy = (e ^x + x ² )dx

Al integrar ambos lados,

∫e ^-y dy = ∫(e ^x + x ² )dx

-e ^-y = e ^x + (x ³ /3) + c (Donde ‘c’ es la constante de integración)

Pregunta 9. x(dy/dx) + y = y ²

Solución:

Tenemos,

x(dy/dx) + y = y ²

x(dy/dx) = y ² – y

[1/(y ² – y)]dy = dx/x

Al integrar ambos lados,

∫[1/(y ² – y)]dy = ∫dx/x

∫[1/(y – 1) – 1/y]dy = ∫(dx/x)

log(y-1) – log(y) = logx + logc

registro[(y – 1)/y] = registro[xc]

(y – 1)/y = xc

(y-1) = yxc (Donde ‘c’ es la constante de integración)

Pregunta 10. (e ^y + 1)cosxdx + e ^y senxdy = 0

Solución:

Tenemos,

(e ^y + 1)cosxdx + e ^y senxdy = 0

(cosx/senx)dx = -[e ^y /(e ^y + 1)]dy

Al integrar ambos lados,

∫(cosx/senx)dx = -∫[e ^y /(e ^y + 1)]dy

log(senx) = -log(e ^y + 1) + log(c)

log(senx) + log(e ^y + 1) = log(c)

log[senx(e ^y + 1)] = log(c)

senx(e ^y + 1) = c (Donde ‘c’ es la constante de integración)

Pregunta 11. xcos ² ydx = ycos ² xdy

Solución:

Tenemos,

xcos ² ydx = ycos ² xdy

(x/cos ² x)dx = (y/cos ² y)dy

xseg ² xdx = yseg ² ydy

Al integrar ambos lados,

∫xseg ² xdx = ∫yseg ² ydy

$x∫sec^2x - ∫[\frac{d(x)}{dx(x)}∫sec^2xdx]dx = y∫sec^2x-∫[\frac{d(y)}{dy}(y)∫sec^2y]dy$

xtanx – ∫tanxdx = ytany – ∫tanydy

xtanx – log(secx) = ytany – log(secy) + c (Donde ‘c’ es la constante de integración)

Pregunta 12. xydy = (y – 1)(x + 1)dx

Solución:

Tenemos,

xydy = (y – 1)(x + 1)dx

[y/(y – 1)]dy = [(x + 1)/x]dx

Al integrar ambos lados,

∫[y/(y – 1)]dy = ∫[(x + 1)/x]dx

∫[1 + 1/(y – 1)]dy = ∫[(x + 1)/x]dx

y + log(y – 1) = x + log(x) + c

y – x = log(x) – log(y – 1) + c (Donde ‘c’ es la constante de integración)

Pregunta 13. x(dy/dx) + coty = 0

Solución:

Tenemos,

x(dy/dx) + coty = 0

x(dy/dx) = -coty

dy/coti = -(dx/x)

tanydy = -(dx/x)

Al integrar ambos lados,

∫tanydy = -∫(dx/x)

log(seguridad) = -log(x) + log(c)

log(seguridad) + log(x) = log(c)

registro (xsecy) = registro (c)

x/acogedor = c

x = c * acogedor (Donde ‘c’ es la constante de integración)

Pregunta 14. (dy/dx) = (xe ^x logx + e ^x )/(xcosy)

Solución:

Tenemos,

(dy/dx) = (xe ^x logx + e ^x )/(xcosy)

xcosydy = (xe ^x logx + e ^x )dx

cosydy = e ^x (logx + 1/x)dx

Al integrar ambos lados,

∫cosydy = ∫e ^x (logx + 1/x)dx

Ya que, ∫[f(x) + f'(x)]e ^x dx] = e ^x f(x)

siny = e ^x logx + c (Donde ‘c’ es la constante de integración)

Pregunta 15. (dy/dx) = e ^x+y + x ³ e ^y

Solución:

Tenemos,

(dy/dx) = e ^x+y + x ³ e ^y

(dy/dx) = e ^x e ^y + x ³ e ^y

dy = e ^y (ex + x ³⁾ dx

e ^-y dy = (e ^x + x ³ )dx

Al integrar ambos lados,

∫e ^-y dy = ∫(e ^x + x ³ )dx

-e ^-y = e ^x + (x ⁴ /4) + c

e ^-y + e ^x + (x ⁴ /4) = c (Donde ‘c’ es la constante de integración)

Pregunta 16. y√(1 + x ² ) + x√(1 + y ² )(dy/dx) = 0

Solución:

Tenemos,

y√(1 + x ² ) + √(1 + y ² )(dy/dx) = 0

y√(1 + x ² )dx = -x√(1 + y ² )dy

$\frac{\sqrt{1+y^2}}{y}dy=-\frac{\sqrt{1+x^2}}{x}dx$

$\frac{y\sqrt{1+y^2}}{y^2}dy=-\frac{x\sqrt{1+x^2}}{x^2}dx$

Al integrar ambos lados,

$∫\frac{y\sqrt{1+y^2}}{y^2}dy=-∫\frac{x\sqrt{1+x^2}}{x^2}dx$

Sea, 1 + y ² = z ²

Al diferenciar ambos lados

2ydy = 2zdz

ydy = zdz

= $∫\frac{y\sqrt{1+y^2}}{y^2}dy$

= $∫\frac{zdz*z}{z^2-1}$

= ∫[z ² /(z ² – 1)]dz

= ∫[1 + 1/(z ² – 1)]dz

= z + (1/2)log[(z – 1)/(z + 1)]

Al poner el valor de z en la ecuación anterior

= $\sqrt{1+y^2}+\frac{1}{2}log[\frac{\sqrt{1+y^2}-1}{\sqrt{1+y^2}+1}]$

Similarmente,

$∫\frac{x\sqrt{1+x^2}}{x^2}dx$ = $\sqrt{1+x^2}+\frac{1}{2}log[\frac{\sqrt{1+x^2}-1}{\sqrt{1+x^2}+1}]$

$\sqrt{1+y^2}+\frac{1}{2}log[\frac{\sqrt{1+y^2}-1}{\sqrt{1+y^2}+1}]=-\sqrt{1+x^2}-\frac{1}{2}log[\frac{\sqrt{1+x^2}-1}{\sqrt{1+x^2}+1}]+c$

$\sqrt{1+y^2}+\sqrt{1+x^2}+\frac{1}{2}log[\frac{\sqrt{1+y^2}-1}{\sqrt{1+y^2}+1}]+\frac{1}{2}log[\frac{\sqrt{1+x^2}-1}{\sqrt{1+x^2}+1}]=c$ (Donde ‘c’ es constante de integración)

Pregunta 17. √(1 + x ² )(dy) + √(1 + y ² )dx = 0

Solución:

Tenemos,

√(1 + x ² )(dy) + √(1 + y ² )dx = 0

$\frac{dy}{\sqrt{(1+y^2)}}=\frac{-dx}{\sqrt{(1+x^2)}}$

Al integrar ambos lados,
log[y + √(1 + y ² )] = -log[x + √(1 + x ² )] + logc

log[y + √(1 + y ² )] + log[x + √(1 + x ² )] = logc

log([y + √(1 + y ² )][x + √(1 + x ² )]) = logc

[y + √(1 + y ² )][x + √(1 + x ² )] = c (Donde ‘c’ es la constante de integración)

Pregunta 18. 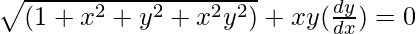$\sqrt{(1 + x^2 + y^2 + x^2y^2)} + xy(\frac{dy}{dx}) = 0$

Solución:

Tenemos,

$\sqrt{(1 + x^2 + y^2 + x^2y^2)} + xy(\frac{dy}{dx}) = 0$

$\sqrt{[(1 + x^2) + y^2(1+x^2)]}+xy(\frac{dy}{dx})=0$

$\sqrt{[(1+x^2)(1+y^2)]}+xy(\frac{dy}{dx})=0$

$\frac{y}{\sqrt{1+y^2}}dy=-\frac{\sqrt{1+x^2}}{x}dx$

$\frac{y}{\sqrt{1+y^2}}dy=-\frac{x\sqrt{1+x^2}}{x^2}dx$

Al integrar ambos lados,

$∫\frac{y}{\sqrt{1+y^2}}dy=-∫\frac{x\sqrt{1+x^2}}{x^2}dx$

Sea, 1 + x ² = z ²

Al diferenciar ambos lados

2xdx = 2zdz

xdx = zdz

= $-∫\frac{x\sqrt{1+x^2}}{x^2}dy$

= $-∫\frac{zdz*z}{z^2-1}$

= -∫[z ² /(z ² – 1)]dz

= -∫[1 + 1/(z ² – 1)]dz

= -z – (1/2)log[(z – 1)/(z + 1)]

Al poner el valor de z en la ecuación anterior

$=-\sqrt{1+x^2}-\frac{1}{2}log[\frac{\sqrt{1+x^2}-1}{\sqrt{1+x^2}+1}]$

Sea, 1 + y ² = v ²

Al diferenciar ambos lados

2ydy = 2vdv

ydy = vdv

= ∫(vdv/v)

=v

Al poner el valor de v en la ecuación anterior

= √(1 + y ² )

= $\sqrt{1+y^2}=-\sqrt{1+x^2}-\frac{1}{2}log[\frac{\sqrt{1+x^2}-1}{\sqrt{1+x^2}+1}]+c$

= $\sqrt{1+y^2}+\sqrt{1+x^2}+\frac{1}{2}log[\frac{\sqrt{1+x^2}-1}{\sqrt{1+x^2}+1}]=c$ (Donde ‘c’ es constante de integración)

Pregunta 19. 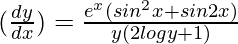$(\frac{dy}{dx}) = \frac{e^x(sin^2x + sin2x)}{y(2logy+1)}$

Solución:

Tenemos,

$(\frac{dy}{dx}) = \frac{e^x(sin^2x + sin2x)}{y(2logy+1)}$

y(2logía + 1)dy = e ^x (sen ² x + sen 2x)dx

Al integrar ambos lados,

∫y(2logía + 1)dy = ∫e ^x (sen ² x + sin2x)dx

$2logy*∫ydy-∫[2\frac{d}{dx}(logy)∫ydy]dy+\frac{y^2}{2}=e^xsin^2x+c$

Ya que, ∫e ^x (sen ² x + sen2x)dx = e ^x sen ² x

Usando la propiedad ∫[f(x) + f'(x)]e ^x = e ^x f(x)

y ² log(y) – ∫ydy + y ² /2 = e ^x sen ² x + c

y ² log(y) – y ² /2 + y ² /2 = e ^x sen ² x + c

y ² log(y) = e ^x sen ² x + c (Donde ‘c’ es la constante de integración)

Pregunta 20. (dy/dx) = x(2logx + 1)/(seno + ycosy)

Solución:

Tenemos,

(dy/dx) = x(2logx + 1)/(seno + ycosy)

(seno + ycosy)dy = x(2logx + 1)dx

Al integrar ambos lados,

∫(seno + ycosy)dy = ∫x(2logx + 1)dx

∫sinydy + y∫cosydy – ∫{(dy/dy)∫cosydy}dy = 2logx∫xdx – 2∫{ $\frac{d(logx)}{dx}$ ∫xdx} + ∫xdx

-cosy + ysiny – ∫sinydy = x ² logx – ∫xdx + (x ² /2) + c

-acogedor + ysiny + acogedor = x ² logx – (x ² /2) + (x ² /2) + c

ysiny = x ² logx + c (Donde ‘c’ es la constante de integración)

Publicación traducida automáticamente

Artículo escrito por vivekray59 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 12 Soluciones RD Sharma – Capítulo 22 Ecuaciones diferenciales – Ejercicio 22.7 | Serie 1

Resuelve las siguientes ecuaciones diferenciales:

Pregunta 1. (x – 1)(dy/dx) = 2xy

Pregunta 2. (x ² + 1)dy = xydx

Pregunta 3. (dy/dx) = (e ^x + 1)y

Pregunta 4. (x – 1)(dy/dx) = 2x ³ y

Pregunta 5. xy(y + 1)dy = (x ² + 1)dx

Pregunta 6. 5(dy/dx) = e ^x y ⁴

Pregunta 7. xcosydy = (xe ^x logx + e ^x )dx

Pregunta 8. (dy/dx) = e ^x+y + x ² e ^y

Pregunta 9. x(dy/dx) + y = y ²

Pregunta 10. (e ^y + 1)cosxdx + e ^y senxdy = 0

Pregunta 11. xcos ² ydx = ycos ² xdy

Pregunta 12. xydy = (y – 1)(x + 1)dx

Pregunta 13. x(dy/dx) + coty = 0

Pregunta 14. (dy/dx) = (xe ^x logx + e ^x )/(xcosy)

Pregunta 15. (dy/dx) = e ^x+y + x ³ e ^y

Pregunta 16. y√(1 + x ² ) + x√(1 + y ² )(dy/dx) = 0

Pregunta 17. √(1 + x ² )(dy) + √(1 + y ² )dx = 0

Pregunta 18. $\sqrt{(1 + x^2 + y^2 + x^2y^2)} + xy(\frac{dy}{dx}) = 0$

Pregunta 19. $(\frac{dy}{dx}) = \frac{e^x(sin^2x + sin2x)}{y(2logy+1)}$

Pregunta 20. (dy/dx) = x(2logx + 1)/(seno + ycosy)

Deja una respuesta Cancelar la respuesta

Resuelve las siguientes ecuaciones diferenciales:

Pregunta 1. (x – 1)(dy/dx) = 2xy

Pregunta 2. (x 2 + 1)dy = xydx

Pregunta 3. (dy/dx) = (e x + 1)y

Pregunta 4. (x – 1)(dy/dx) = 2x 3 y

Pregunta 5. xy(y + 1)dy = (x 2 + 1)dx

Pregunta 6. 5(dy/dx) = e x y 4

Pregunta 7. xcosydy = (xe x logx + e x )dx

Pregunta 8. (dy/dx) = e x+y + x 2 e y

Pregunta 9. x(dy/dx) + y = y 2

Pregunta 10. (e y + 1)cosxdx + e y senxdy = 0

Pregunta 11. xcos 2 ydx = ycos 2 xdy

Pregunta 12. xydy = (y – 1)(x + 1)dx

Pregunta 13. x(dy/dx) + coty = 0

Pregunta 14. (dy/dx) = (xe x logx + e x )/(xcosy)

Pregunta 15. (dy/dx) = e x+y + x 3 e y

Pregunta 16. y√(1 + x 2 ) + x√(1 + y 2 )(dy/dx) = 0

Pregunta 17. √(1 + x 2 )(dy) + √(1 + y 2 )dx = 0

Pregunta 18.

Pregunta 19.

Pregunta 20. (dy/dx) = x(2logx + 1)/(seno + ycosy)

Deja una respuesta Cancelar la respuesta

Pregunta 2. (x ² + 1)dy = xydx

Pregunta 3. (dy/dx) = (e ^x + 1)y

Pregunta 4. (x – 1)(dy/dx) = 2x ³ y

Pregunta 5. xy(y + 1)dy = (x ² + 1)dx

Pregunta 6. 5(dy/dx) = e ^x y ⁴

Pregunta 7. xcosydy = (xe ^x logx + e ^x )dx

Pregunta 8. (dy/dx) = e ^x+y + x ² e ^y

Pregunta 9. x(dy/dx) + y = y ²

Pregunta 10. (e ^y + 1)cosxdx + e ^y senxdy = 0

Pregunta 11. xcos ² ydx = ycos ² xdy

Pregunta 14. (dy/dx) = (xe ^x logx + e ^x )/(xcosy)

Pregunta 15. (dy/dx) = e ^x+y + x ³ e ^y

Pregunta 16. y√(1 + x ² ) + x√(1 + y ² )(dy/dx) = 0

Pregunta 17. √(1 + x ² )(dy) + √(1 + y ² )dx = 0

Pregunta 18. $\sqrt{(1 + x^2 + y^2 + x^2y^2)} + xy(\frac{dy}{dx}) = 0$

Pregunta 19. $(\frac{dy}{dx}) = \frac{e^x(sin^2x + sin2x)}{y(2logy+1)}$