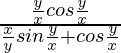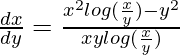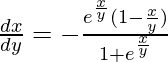Pregunta 14. 3x 2 dy = (3xy + y 2 )dx
Solución:
Tenemos,
3x 2 dy = (3xy + y 2 )dx
(dy/dx) = (3xy + y 2 )/3x 2
es una ecuacion homogenea
Entonces pon y = vx (i)
dy/dx = v + x(dv/dx)
Asi que,
v + x(dv/dx) = (3xvx + v 2 x 2 )/3x 2
v + x(dv/dx) = (3v + v2 ) /3
x(dv/dx) = [(3v + v 2 )/3] – v
x(dv/dx) = (3v + v2 – 3v)/3
3(dv/v 2 ) = (dx/x)
Al integrar ambos lados,
3∫(dv/v 2 ) = ∫(dx/x)
-(3/v) = log|x| +c
-3x/y = log(x) + c (Donde ‘c’ es la constante de integración)
Pregunta 15. (dy/dx) = x/(2y + x)
Solución:
Tenemos,
(dy/dx) = x/(2y + x)
es una ecuacion homogenea
Entonces, pon y = vx (i)
dy/dx = v + x(dv/dx)
Asi que,
v + x(dv/dx) = x/(2vx + x)
v + x(dv/dx) = 1/(2v + 1)
x(dv/dx) = [1/(2v + 1)] – v
x(dv/dx) = (1 – 2v 2 – v)/(2v + 1)
(2v + 1)dv/(2v 2 + v – 1) = -(dx/x)
Al integrar ambos lados,
∫(2v + 1)dv/(2v 2 + v – 1) = -∫(dx/x)
Resolviendo por fracción parcial,
A(v + 1) + B(2v – 1) = (2v + 1) (yo)
Poniendo v = -1 y resuelve la ecuación anterior,
A(0) + B(-3) = (-1)
B = (1/3)
Poniendo v = -(1/2) y resuelve la ecuación (i),
A(3/2) + B(0) = 2
A = (4/3)
(3/2)log|2v – 1| + (1/3)log|v + 1| = -log|x| + log|c|
registro|(2v – 1) 2 (v + 1)| = -log|x| 3 + registro|c|
|(2v – 1) 2 (v + 1)| = (c/x 3 )
(2y/x – 1) 2 (y/x + 1) = (c/x 3 )
(2y – x) 2 (x + y) = c (Donde ‘c’ es la constante de integración)
Pregunta 16. (x + 2y)dx – (2x – y)dy = 0
Solución:
Tenemos,
(x + 2y)dx – (2x – y)dy = 0
(dy/dx) = (x + 2y)/(2x – y)
es una ecuacion homogenea
Entonces, pon y = vx (i)
dy/dx = v + x(dv/dx)
Asi que,
v + x(dv/dx) = (x + 2vx)/(2x – vx)
v + x(dv/dx) = (1 + 2v)/(2 – v)
x(dv/dx) = [(1 + 2v)/(2 – v)] – v
x(dv/dx) = (1 + 2v – 2v + v 2 )/(2 – v)
(2 – v)dv/(1 + v2 ) = (dx/x)
Al integrar ambos lados,
∫(2 – v)dv/(1 + v 2 ) = ∫(dx/x)
2∫dv/(1 + v 2 ) – ∫vdv/(1 + v 2 ) = log|x| + log|c|
2tan -1 v – (1/2)∫2vdv/(1 + v 2 ) = log|x| + log|c|
2tan -1 v – log|1 + v 2 | 1/2 = registro|cx|
2tan -1 v = log|cx√(1 + v 2 )|
(Donde ‘c’ es constante de integración)
Pregunta 17. 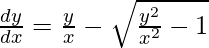
Solución:
Tenemos,
es una ecuacion homogenea
Entonces, pon y = vx (i)
dy/dx = v + x(dv/dx)
Asi que,
v + x(dv/dx) = (vx/x) – √(v 2 x 2 /x 2 – 1)
v + x(dv/dx) = v – √(v 2 – 1)
x(dv/dx) = -√(v 2 – 1)
dv/√(v 2 – 1) = -(dx/x)
Al integrar ambos lados,
∫dv/√(v 2 – 1) = -∫(dx/x)
log|v + √(v 2 – 1)| = -log|x| + log|c|
|v + √(v 2 – 1)| = (c/x)
y + √(y 2 – x 2 ) = c (Donde ‘c’ es la constante de integración)
Pregunta 18. (dy/dx) = (y/x){log(y) – log(x) + 1}
Solución:
Tenemos,
(dy/dx) = (y/x){log(y) – log(x) + 1}
(dy/dx) = (y/x){log(y/x) + 1}
es una ecuacion homogenea
Entonces, pon y = vx (i)
dy/dx = v + x(dv/dx)
Asi que,
v + x(dv/dx) = v{log(v) + 1}
v + x(dv/dx) = vlog(v) + v
x(dv/dx) = vlog(v)
dv/vlogv = (dx/x)
Al integrar ambos lados,
∫dv/vlogv = ∫(dx/x)
Sea, logv = z
dv/v = dz
∫(dz/z) = ∫(dx/x)
registro|z| = registro|x| + log|c|
z = xc
registro|v| = xc
log|y/x| = xc (Donde ‘c’ es la constante de integración)
Pregunta 19. (dy/dx) = (y/x) + sin(y/x)
Solución:
Tenemos,
(dy/dx) = (y/x) + sin(y/x)
es una ecuacion homogenea
Entonces, pon y = vx (i)
dy/dx = v + x(dv/dx)
Asi que,
v + x(dv/dx) = v + sin(v)
x(dv/dx) = sen(v)
dv/sen(v) = (dx/x)
Al integrar ambos lados,
∫dv/sen(v) = ∫(dx/x)
∫coseg(v)dv = ∫(dx/x)
registro|bronceado(v/2)| = registro (x) + registro (c)
registro|bronceado(y/2x)| = registro|xc|
tan(y/2x) = |xc| (Donde ‘c’ es constante de integración)
Pregunta 20. y 2 dx + (x 2 – xy + y 2 )dy = 0
Solución:
Tenemos,
y 2 dx + (x 2 – xy + y 2 )dy = 0
(dy/dx) = -(y 2 )/(x 2 – xy + y 2 )
es una ecuacion homogenea
Entonces, pon y = vx (i)
dy/dx = v + x(dv/dx)
Asi que,
v + x(dv/dx) = -(v 2 x 2 )/(x 2 – xvx + v 2 x 2 )
v + x(dv/dx) = -(v 2 )/(1 – v + v 2 )
y(dv/dx) = [-(v 2 )/(1 – v + v 2 )] – v
Al integrar ambos lados,
∫dv/(1 + v 2 ) – ∫dv/v = ∫(dx/x)
tan -1 (v) – log(v) = log(x) + log(c)
bronceado -1 (y/x) – log|y/x| = registro(xc)
tan -1 (y/x) = log|(y/x)xc|
tan -1 (y/x) = log|yc|
(Donde ‘c’ es constante de integración)
Pregunta 21. [x√(x 2 + y 2 ) – y 2 ]dx + xydy = 0
Solución:
Tenemos,
[x√(x 2 + y 2 ) – y 2 ]dx + xydy = 0
dy/dx = -[x√(x 2 + y 2 ) – y 2 ]/xy
dy/dx = [y 2 – x√(x 2 + y 2 )]/xy
es una ecuacion homogenea
Entonces, pon y = vx (i)
dy/dx = v + x(dv/dx)
Asi que,
v + x(dv/dx) = [v 2 x 2 – x√(x 2 + v 2 x 2 )]/xvx
v + x(dv/dx) = [v 2 – √(1 + v 2 )]/v
x(dv/dx) = [v 2 – √(1 + v 2 )]/v – v
x(dv/dx) = -(√(1 + v 2 )/v
vdv/√(1 + v2 ) = -(dx/x)
Al integrar ambos lados,
∫vdv/√(1 + v 2 ) = -∫(dx/x)
(1/2)∫2vdv/√(1 + v 2 ) = -∫(dx/x)
Sea, 1 + v 2 = z
2vdv = dz
(1/2)∫dz/√z = -∫(dx/x)
√z = -log|x| + log|c|
√(1 + v 2 ) = log|c/x|
√(x 2 + y 2 )/x = log|c/x|
√(x 2 + y 2 ) = xlog|c/x| (Donde ‘c’ es constante de integración)
Pregunta 22. x(dy/dx) = y – xcos 2 (y/x)
Solución:
Tenemos,
x(dy/dx) = y – xcos 2 (y/x)
(dy/dx) = y/x – cos 2 (y/x)
es una ecuacion homogenea
Entonces, pon y = vx (i)
dy/dx = v + x(dv/dx)
Asi que,
v + x(dv/dx) = v – cos 2 (v)
x(dv/dx) = -cos 2 (v)
dv/cos 2 (v) = -(dx/x)
Al integrar ambos lados,
∫dv/cos 2 (v) = -∫(dx/x)
∫seg 2 vdv = -∫(dx/x)
tan(v) = -log|x| + log|c|
tan(y/x) = log|c/x| (Donde ‘c’ es constante de integración)
Pregunta 23. (y/x)cos(y/x)dx – {(x/y)sen(y/x) + cos(y/x)}dy = 0
Solución:
Tenemos,
(y/x) cos(y/x)dx – {(x/y)sen(y/x) + cos(y/x)}dy = 0
es una ecuacion homogenea
Entonces, pon y = vx (i)
dy/dx = v + x(dv/dx)
Asi que,
x(dv/dx) = (v 2 cosv – vsinv – v 2 cosv)/(senv + vcosv)
x(dv/dx) = -vsenv/(senv + vcosv)
Al integrar ambos lados,
∫[(senv + vcosv)/vsenv]dv = -∫(dx/x)
∫(dv/v) + ∫(cotv)dv = -∫(dx/x)
registro|v| + log|sinv| = -log|x| + log|c|
log|vsinv| = registro|c/x|
(y/x)sen(y/x) = (c/x)
ysen(y/x) = c (Donde ‘c’ es la constante de integración)
Pregunta 24. xylog(x/y)dx + {y 2 – x 2 log(x/y)}dy = 0
Solución:
Tenemos,
xlog(x/y)dx + {y 2 – x 2 log(x/y)}dy = 0
es una ecuacion homogenea
Entonces, pon x = vy (i)
y,
dx/dy = v + y(dv/dy)
Asi que,
v + y(dv/dy) = (v 2 logv – 1)/(vlogv)
y(dv/dy) = [(v 2 logv – 1)/(vlogv)] – v
y(dv/dy) = (v 2 logv – 1 – v 2 logv)/vlogv
y(dv/dy) = -(1/vogv)
vlogvdv = -(día/año)
Al integrar ambos lados,
∫vlogvdv = -∫(dy/y)
logv∫vdv – ∫{d/dv(logv)∫vdv}dv}dv = -∫(dy/y)
(v 2 /2)logv – (1/2)∫(1/v)(v 2 /2)dv = -logía + logc
(v 2 /2)logv – (1/2)∫vdv = -logía + logc
(v 2 /2) logv – (v 2 /4) + logía = log|c|
(v 2 /2)[logv – 1/2] + logía = log|c|
v 2 [logv – (1/2)] + logía= log|c|
(x 2 /y 2 )[log(x/y) – (1/2)] + logía= log|c| (Donde ‘c’ es constante de integración)
Pregunta 25. (1 + e x/y )dx + e x/y (1 – x/y)dy = 0
Solución:
Tenemos,
(1 + e x/y )dx + e x/y (1 – x/y)dy = 0
es una ecuacion homogenea
Entonces, pon x = vy (i)
y,
dx/dy = v + y(dv/dy)
Asi que,
y(dv/dy) = -[e v (1 – v)/(1 + e v )] – v
y(dv/dy) = (-e v + ve v – v – ve v )/(1 + e v )
y(dv/dy) = -(v + ve v )/(1 + e v )
[(1 + e v )/(v + e v )]dv = -(dy/y)
Al integrar ambos lados,
∫[(1 + e v )/(v + e v )]dv = -∫(dy/y)
log|(v + e v )| = -log(y) + log(c)
log|(v + e v )| = registro|c/y|
(x/y) + e x/y = c/y
x + ye x/y = c (Donde ‘c’ es la constante de integración)
Pregunta 26. (x 2 + y 2 )dy/dx = (8x 2 – 3xy + 2y 2 )
Solución:
Tenemos,
(x 2 + y 2 )dy/dx = (8x 2 – 3xy + 2y 2 )
(dy/dx) = (8x 2 – 3xy + 2y 2 )/(x 2 + y 2 )
es una ecuacion homogenea
Entonces, pon y = vx (i)
X,
dy/dx = v + x(dv/dx)
Asi que,
v + x(dv/dx) = (8x 2 – 3xvx + 2v 2 x 2 )/(x 2 + v 2 x 2 )
v + x(dv/dx) = (8 – 3v + 2v 2 )/(1 + v 2 )
x(dv/dx) = [(8 – 3v + 2v 2 )/(1 + v 2 )] – v
x(dv/dx) = (8 – 4v + 2v 2 – v 3 )/(1 + v 2 )
(1 + v 2 )dv/(8 – 4v + 2v 2 – v 3 ) = (dx/x)
Al integrar ambos lados,
Usando fracciones parciales,
(1 + v 2 ) = Av(2 – v) + B(2 – v) + C(4 + v 2 )
(1 + v 2 ) = 2Av – Av 2 + 2B – Bv + 4C+ Cv 2
(1 + v 2 ) = (C – A)v 2 + (2A – B)v + (2B + 4C)
Comparando el coeficiente de ambos lados,
(C-A) = 1
(2A-B) = 0
(2B + 4C) = 1
Resolviendo las ecuaciones anteriores,
A = -(3/8)
B = -(3/4)
C = (5/8)
(Donde ‘c’ es constante de integración)
Publicación traducida automáticamente
Artículo escrito por vivekray59 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA