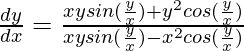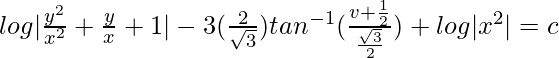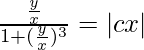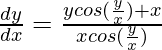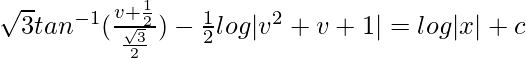Clase 12 Soluciones RD Sharma – Capítulo 22 Ecuaciones diferenciales – Ejercicio 22.9

Pregunta 27. (x ² – 2xy)dy + (x ² – 3xy + 2y ² )dx = 0

Solución:

Tenemos,

(x2 – ^2xy )dy + (x2 – 3xy ⁺ 2y2 )dx = ⁰

(dy/dx) = (x2 – 3xy ⁺ 2y2 )/(2xy ^–^y2 )

es una ecuacion homogenea

Entonces, pon y = vx (i)

dy/dx = v + x(dv/dx)

Asi que,

v + x(dv/dx) = (x ² – 3xvx + 2v ² x ² )/(2xvx – x ² )

v + x(dv/dx) = (1 – 3v + 2v ² )/(2v – 1)

x(dv/dx) = [(1 – 3v + 2v ² )/(2v – 1)] – v

x(dv/dx) = (1 – 3v + 2v ² – 2v ² + v)/(2v – 1)

x(dv/dx) = (1 – 2v)/(2v – 1)

x(dv/dx) = -1

dv = -(dx/x)

Al integrar ambos lados,

∫dv = -∫(dx/x)

v = -log|x| + log|c|

(y/x) + log|x| = registro|c| (Donde ‘c’ es constante de integración)

Pregunta 28. x(dy/dx) = y – xcos ² (y/x)

Solución:

Tenemos,

x(dy/dx) = y – xcos ² (y/x)

(dy/dx) = y/x – cos ² (y/x)

es una ecuacion homogenea

Entonces, pon y = vx (i)

dy/dx = v + x(dv/dx)

Asi que,

v + x(dv/dx) = v – cos ² (v)

x(dv/dx) = -cos ² (v)

dv/cos ² (v) = -(dx/x)

Al integrar ambos lados,

∫dv/cos ² (v) = -∫(dx/x)

∫seg ² vdv = -∫(dx/x)

tan(v) = -log|x| + log|c|

tan(y/x) = log|c/x| (Donde ‘c’ es constante de integración)

Pregunta 29. x(dy/dx) – y = 2√(y ² – x ² )

Solución:

Tenemos,

x(dy/dx) – y = 2√(y ² – x ² )

(dy/dx) = [2√(y ² – x ² ) + y]/x

es una ecuacion homogenea

Entonces, pon y = vx (i)

dy/dx = v + x(dv/dx)

Asi que,

$v+x\frac{dv}{dx}=\frac{2\sqrt{v^2x^2-x^2}+vx}{x}$

$v+x\frac{dv}{dx}=2\sqrt{v^2-1}+v$

x(dv/dx) = 2√(v ² – 1)

dv/√(v ² – 1) = 2(dx/x)

Al integrar ambos lados,

∫dv/√(v ² – 1) = 2∫(dx/x)

log|v + √(v ² – 1)| = 2log(x) + log(c)

|v + √(v ² – 1)| = |cx ² |

$\frac{y}{x}+\sqrt{\frac{y^2}{x^2}-1}=|cx^2|$

$y+\sqrt{y^2-x^2}=cx^3$ (Donde ‘c’ es constante de integración)

Pregunta 30. xcos(y/x)(ydx + xdy) = ysen(y/x)(xdy – ydx)

Solución:

Tenemos,

xcos(y/x)(ydx + xdy) = ysen(y/x)(xdy – ydx)

xycos(y/x)dx + x ² cos(y/x)dy = xysen(y/x)dy – y ² sen(y/x)dx

x ² cos(y/x)dy – xysen(y/x)dy = -y ² sen(y/x)dx – xycos(y/x)dx

$\frac{dy}{dx}=\frac{xysin(\frac{y}{x})+y^2cos(\frac{y}{x})}{xysin(\frac{y}{x})-x^2cos(\frac{y}{x})}$

es una ecuacion homogenea

Entonces, pon y = vx (i)

dy/dx = v + x(dv/dx)

Asi que,

$v+x\frac{dv}{dx}=\frac{xvxsinv+v^2x^2cosv}{xvxsinv-x^2cosv}$

v + x(dv/dx) = (vcosv + v ² senv)/(v senv – cosv)

x(dv/dx) = [(vcosv + v ² senv)/(vsenv – cosv)] – v

x(dv/dx) = (vcosv + v ² senv – v ² senv + vcosv)/(v senv – cosv)

x(dv/dx) = (2vcosv)/(vsenv – cosv)

[(vsinv – cosv)/(vcosv)]dv = 2(dx/x)

Al integrar ambos lados,

∫tanvdv – ∫(dv/v) = 2log|x| + log|c|

log|seg| – registro|v| = registro|cx ² |

log|(segv/v)| = registro|cx ² |

(x/y)seg(y/x) = cx ²

sec(y/x) = cxy (Donde ‘c’ es la constante de integración)

Pregunta 31. (x ² + 3xy + y ² )dx – x ² dy = 0

Solución:

Tenemos,

(x ² + 3xy + y ² )dx – x ² dy = 0

dy/dx = (x2 ⁺ 3xy + y2 ⁾^/ x2

es una ecuacion homogenea

Entonces, pon y = vx (i)

dy/dx = v + x(dv/dx)

Asi que,

v + x(dv/dx) = (x ² + 3xvx + v ² x ² )/x ²

v + x(dv/dx) = (1 + 3v + v ² )

x(dv/dx) = (1 + 3v + v ² ) – v

x(dv/dx) = (1 + 2v + v ² )

x(dv/dx) = (1 + v) ²

dv/(1 + v) ² = (dx/x)

Al integrar ambos lados,

∫dv/(1 + v) ² = ∫(dx/x)

-[1/(v + 1)] = log|x| – C

$-\frac{1}{\frac{y}{x}+1}=log|x|-c$

x/(x + y) + log|x| = c (Donde ‘c’ es una constante de integración)

Pregunta 32. (x – y)(dy/dx) = (x + 2y)

Solución:

Tenemos,

(x – y)(dy/dx) = (x + 2y)

(dy/dx) = (x + 2y)/(x – y)

es una ecuacion homogenea

Entonces, pon y = vx (i)

dy/dx = v + x(dv/dx)

Asi que,

v + x(dv/dx) = (x + 2vx)/(x – vx)

v + x(dv/dx) = (1 + 2v)/(1 – v)

x(dv/dx) = [(1 + 2v)/(1 – v)] – v

x(dv/dx) = (1 + 2v – v + v ² )/(1 – v)

x(dv/dx) = (1 + v + v ² )/(1 – v)

(1 – v)dv/(1 + v + v ² ) = (dx/x)

Al integrar ambos lados,

∫[(1 – v)/(1 + v + v ² )]dv = ∫(dx/x)

$-\frac{1}{2}∫\frac{2v-2}{v^2+v+1}dv=∫\frac{dx}{x}$

$∫\frac{(2v+1)-3}{v^2+v+1}dv=-2∫\frac{dx}{x}$

$∫\frac{2v+1}{v^2+v+1}dv-∫\frac{3dv}{v^2+2v(\frac{1}{2})+(\frac{1}{2})^2-(\frac{1}{2})^2+1}=-2log|x|+c$

$log|v^2+v+1|-∫\frac{3dv}{(v+\frac{1}{2})^2+(\frac{\sqrt{3}}{2})^2}=-log|x^2|+c$

$log|\frac{y^2}{x^2}+\frac{y}{x}+1|-3(\frac{2}{\sqrt{3}})tan^{-1}(\frac{v+\frac{1}{2}}{\frac{\sqrt{3}}{2}})+log|x^2|=c$

$log|y^2+xy+x^2|=2\sqrt{3}tan^{-1}(\frac{2y+x}{x\sqrt{3}})+c$ (Donde ‘c’ es una constante de integración)

Pregunta 33. (2x ² y + y ³ )dx + (xy ² – 3x ² )dy = 0

Solución:

Tenemos,

(2x ² y + y ³ )dx + (xy ² – 3x ² )dy = 0

dy/dx = (2x ² y + y ³ )/(3x ³ – xy ² )

es una ecuacion homogenea

Entonces, pon y = vx (i)

dy/dx = v + x(dv/dx)

Asi que,

v + x(dv/dx) = (2x ² vx + v ³ x ³ )/(3x ³ – xv ² x ² )

v + x(dv/dx) = (2v + v3 )/(3 ^–^v3 )

x(dv/dx) = [(2v + v ³ )/(3 – v ³ )] – v

x(dv/dx) = (2v + v3 – 3v + v3 ⁾ /(3 ^–^v3 )

(3 – v ³ )dv/(2v ³ – v) = (dx/x)

Al integrar ambos lados,

∫[(3 – v ³ )/(2v ³ – v)]dv = ∫(dx/x)

$∫\frac{3-v^2}{v(2v^2-1)}dv=∫\frac{dx}{x}$

Usando fracciones parciales,

$\frac{3-v^2}{v(2v^2-1)}=\frac{A}{v}+\frac{Bv+C}{2v^2-1}$

3 – v ² = A(2v ² – 1) + (Bv + C)v

3 – v ² = 2Av ² – A + Bv ² + Cv

3 – v ² = v ² (2A + B) + Cv – A

Al comparar los coeficientes, obtenemos

A = -3,

B = 5,

C = 0,

$-3∫\frac{dv}{v}+∫\frac{5v}{2v^2-1}dv=∫\frac{dx}{x}$

$-3∫\frac{dv}{v}+\frac{5}{4}∫\frac{4v}{2v^2-1}dv=∫\frac{dx}{x}$

-3log|v|+(5/4)log|2v ² -1|=log|x|+log|c|

-12log|v|+5log|2v ² -1|=4log|x|+4log|c|

$log|\frac{2v^2-1}{v^{12}}|=log|x^4c^4|$

$(2\frac{y^2}{x^2}-1)^5=x^4c^4\frac{y^{12}}{x^{12}}$

$\frac{2y^2-x^2}{x^{10}}=x^4c^4\frac{y^{12}}{x^{12}}$

| 2y2 ^– x2 ^|⁵ = x ² c ⁴ y ¹² (Donde ‘c’ es una constante de integración)

Pregunta 34. x(dy/dx) – y + xsen(y/x) = 0

Solución:

Tenemos,

x(dy/dx) – y + xsen(y/x) = 0
x(dy/dx) = y – xsen(y/x)

(dy/dx) = [y – xsen(y/x)]/x

es una ecuacion homogenea

Entonces, pon y = vx (i)

dy/dx = v + x(dv/dx)

Asi que,

v + x(dv/dx) = [vx – xsenv]/x

v + x(dv/dx) = (v – senv)

x(dv/dx) = -senv

cosecvdv = -(dx/x)

Al integrar ambos lados,

∫cosecvdv = -∫(dx/x)

-log|cosecv + cotv| = -log|x| + log|c|

-log|(1/senv) + (cosv/senv)| = -log|x/c|

|(1 + cosv)/senv| = |x/c|

xsenv = c(1 + cosv)

xsen(y/x) = c[1 + cos(y/x)] (Donde ‘c’ es la constante de integración)

Pregunta 35. ydx + {xlog(y/x)}dy – 2xydy = 0

Solución:

Tenemos,

ydx + {xlog(y/x)}dy – 2xydy = 0

y + {xlog(y/x)}(dy/dx) – 2xy = 0

$\frac{dy}{dx}=\frac{y}{2x-xlog(\frac{y}{x})}$

es una ecuacion homogenea

Entonces, pon y = vx (i)

dy/dx = v + x(dv/dx)

Asi que,

$v+x\frac{dv}{dx}=-\frac{vx}{2x-xlogv}$

v + x(dv/dx) = v/(2 – logv)

x(dv/dx) = [v/(2 – logv)] – v

x(dv/dx) = (v – 2v + vlogv)/(2 – logv)

x(dv/dx) = -v(logv – 1)/(logv – 2)

$\frac{(logv-2)}{v(logv-1)}dv=-\frac{dx}{x}$

Al integrar ambos lados,

$∫\frac{(logv-2)}{v(logv-1)}dv=-∫\frac{dx}{x}$

$∫\frac{(logv-1)-1}{v(logv-1)}dv=-∫\frac{dx}{x}$

$∫\frac{dv}{v(logv-1)}-∫\frac{dv}{v(logv-1)}=-∫\frac{dx}{x}$

Dejar. logv – 1 = z

Al diferenciar ambos lados,

(dv/v) = dz

∫dz – ∫(dz/z) = -∫(dx/x)

z – log|z| = -log|x| + log|c|

(logv – 1) – log|(logv – 1)| = -log|x| + log|c|

logv – log|logv – 1| = -log|x| + log|c| + 1

log|(logv – 1)/v| = registro|c ₁ x|

|logv – 1| = |c _1xv |

|registro(y/x) – 1| = |c 1x(y/x) _|

|registro(y/x) – 1| = |c ₁ y| (Donde ‘c ₁ ‘ es la constante de integración)

Pregunta 36(i). (x2 + ^{y2 )dx}⁼ 2xydy, y(1) = 0

Solución:

Tenemos,

(x2 + ^{y2 )dx}⁼ 2xydy

(dy/dx) = (x2 + ^y2 )/ ^2xy

es una ecuacion homogenea

Entonces, pon y = vx (i)

dy/dx = v + x(dv/dx)

Asi que,

^{v +} x(dv/dx) = ( ^x2⁺ v2x2 ) / ^2vx2

v + x(dv/dx) = (1 + v2 ⁾ /2v

x(dv/dx) = [(1 + v ² )/2v] – v

x(dv/dx) = (1 + ^v2 – 2v2 ⁾ /2v

x(dv/dx) = (1 – v2 ⁾ /2v

2vdv/(1 – v ² ) = (dx/x)

Al integrar ambos lados,

∫2vdv/(1 – v ² ) = ∫(dx/x)

-log|1 – v ² | = registro|x| – registro|c|

registro|1 – v ² | = registro|c/x|

|1 – y ² /x ² | = |c/x|

|x ² – y ² | = |xx|

En x = 1, y = 0

1 – 0 = c

c = 1

|x ² – y ² | = |x|

(x ² – y ² ) = x

Pregunta 36(ii). xe ^x/y – y + x(dy/dx) = 0, y(e) = 0

Solución:

Tenemos,

xe ^x/y – y + x(dy/dx) = 0

(dy/dx) = (y – xe ^x/y )/x

es una ecuacion homogenea

Entonces, pon y = vx (i)

dy/dx = v + x(dv/dx)

Asi que,

v + x(dv/dx) = (vx – xe ^v )/x

v + x(dv/dx) = v – e ^v

x(dv/dx) = v – e ^v – v

x(dv/dx) = -e ^v

e ^-v dv = -(dx/x)

Al integrar ambos lados,

∫e ^-v dv = -∫(dx/x)

-e ^-v = -log|x| – registro|c|

e ^-v = log|x| + log|c|

e ^-(y/x) = log|x| + log|c|

En x = e, y = 0

e ^-(0/e) = log|e| + log|c|

1 = 1 + registro|c|

c = 0

e ^-y/x = logx

Pregunta 36(iii). (dy/dx) – (y/x) + cosec(y/x) = 0, y(1) = 0

Solución:

Tenemos,

(dy/dx) – (y/x) + cosec(y/x) = 0

(dy/dx) = (y/x) – cosec(y/x)

es una ecuacion homogenea

Entonces, pon y = vx (i)

dy/dx = v + x(dv/dx)

Asi que,

v + x(dv/dx) = v – cosec(v)

x(dv/dx) = v – cosec(v) – v

x(dv/dx) = -cosec(v)

-sen(v)dv = (dx/x)

Al integrar ambos lados,

-∫sen(v)dv = ∫(dx/x)

cos(v) = log|x| + log|c|

cos(y/x) = log|x| + log|c|

En x = 1, y = 0

cos(0/1) = registro|1| + log|c|

1 = 0 + registro|c|

registro|c| = 1

cos(y/x) = log|x| + 1

registro|x| = cos(y/x) – 1

Pregunta 36(iv). (xy – y ² )dx – x ² dy = 0, y(1) = 1

Solución:

Tenemos,

(xy – y ² )dx – x ² dy = 0

(dy/dx) = (xy – y ² )/x ²

(dy/dx) = (y/x) – (y ² /x ² )

es una ecuacion homogenea

Entonces, pon y = vx (i)

dy/dx = v + x(dv/dx)

Asi que,

v + x(dv/dx) = v – v ²

x(dv/dx) = v – v ² – v

x(dv/dx) = -v ²

-(dv/v ² ) = (dx/x)

Al integrar ambos lados,

-∫(dv/v ² ) = ∫(dx/x)

-(-1/v) = registro|x| +c

(1/v) = registro|x| +c

x/y = registro|x| +c

En x = 1, y = 1

1 = registro|1| +c

c = 1

x/y = registro|x| + 1

y = x/[registro|x| + 1]

Pregunta 36(v). (dy/dx) = [y(x + 2y)]/[x(2x + y)]

Solución:

Tenemos,

(dy/dx) = [y(x + 2y)]/[x(2x + y)]

es una ecuacion homogenea

Entonces, pon y = vx (i)

dy/dx = v + x(dv/dx)

Asi que,

v + x(dv/dx) = [vx(x + 2vx)]/[x(2x + vx]

x(dv/dx) = [vx(x + 2vx)]/[x(2x + vx] – v

x(dv/dx) = (v + 2v ² – 2v – v ² )/(2 + v)

x(dv/dx) = (v ² – v)/(2 + v)

(2 + v)dv/[v(v – 1)] = (dx/x)

Al integrar ambos lados,

$∫\frac{2+v}{v(v-1)}dv=\frac{dx}{x}$

Usando derivada parcial,

$\frac{2+v}{v(v-1)}dv=\frac{A}{v}+\frac{B}{v-1}$

2 + v = A(v – 1) + B(v)

2 + v = v(A + B) – A

Al comparar los coeficientes,

A = -2

B = 3

-2∫(dv/v) + 3∫dv/(v – 1) = ∫(dx/x)

-2log|v| + 3log|v – 1| = registro|x| + log|c|

log|(v – 1) ³ /v ² | = registro|xc|

(v – 1) ³ = v ² |xc|

(y – x) ³ /x ³ = (y/x) ² |xc|

(y – x) ³ = y ² x ² c

En x = 1, y = 2,

(2 – 1) ³ = 4 * 1 * c

c = (1/4)

(y – x) ³ = (1/4)y ² x ²

Pregunta 36 (vi). (y ⁴ – 2x ³ y)dx + (x ⁴ – 2xy ³ )dy = 0, y(1) = 0

Solución:

Tenemos,

(y ⁴ – 2x ³ y)dx + (x ⁴ – 2xy ³ )dy = 0

dy/dx = (2x ³ y – y ⁴ )/(x ⁴ – 2xy ³ )

es una ecuacion homogenea

Entonces, pon y = vx (i)

dy/dx = v + x(dv/dx)

Asi que,

v + x(dv/dx) = (2x ³ vx – v ⁴ x ⁴ )/(x ⁴ – 2xv ³ x ³ )

v + x(dv/dx) = (2v – v ⁴ )/(1 – 2v ³ )

x(dv/dx) = [(2v – v ⁴ )/(1 – 2v ³ )] – v

x(dv/dx) = (2v – v ⁴ – v + 2v ⁴ )/(1 – 2v ³ )

x(dv/dx) = (v + v ⁴ )/(1 – 2v ³ )

$\frac{1-2v^3}{v(1+v^3)}dv=\frac{dx}{x}$

$\frac{1+v^3-3v^3}{v(1+v^3)}dv=\frac{dx}{x}$

Al integrar ambos lados,

$∫\frac{1+v^3}{v(1+v^3)}dv-∫\frac{3v^3}{v(1+v^3)}dv=∫\frac{dx}{x}$

∫(dv/v) – ∫(3v ² )dv/(1 + v ³ ) = log|x| + log|c|

registro|v| – registro|1 + v ³ | = registro|xc|

log|v/(1 + v ³ )| = registro|xc|

$\frac{\frac{y}{x}}{1+(\frac{y}{x})^3}=|cx|$

En x = 1, y = 1,

1/(1 + 1) = c

c = (1/2)

(yx ² )/(x ³ + y ³ ) = (1/2)x

Pregunta 36 (vii). x(x ² + 3y ² )dx + y(y ² + 3x ² )dy = 0, y(1) = 1

Solución:

Tenemos,

x(x ² + 3y ² )dx + y(y ² + 3x ² )dy = 0

dy/dx = -[x(x ² + 3y ² )/y(y ² + 3x ² )]

es una ecuacion homogenea

Entonces, pon y = vx (i)

dy/dx = v + x(dv/dx)

Asi que,

$v+x\frac{dv}{dx}=-\frac{x(x^2+3v^2x^2)}{vx(v^2x^2+3x^2)}$

$v+x\frac{dv}{dx}=-\frac{(1+3v^2)}{v(v^2+3)}$

$x\frac{dv}{dx}=-\frac{(1+3v^2)}{v(v^2+3)}-v$

x(dv/dx) = -(1 + 3v ² + v ⁴ + 3v ² )/v(v ² + 3)

[(v ³ + 3v)/(1 + 6v ² + v ⁴ )]dv = -(dx/x)

Multiplica ambos lados por 4 e integrando,

$∫\frac{4v^3+12v}{v^4+6v^2+1}dv=-4∫\frac{dx}{x}$

registro|v ⁴ + 6v ² + 1| = -log|x| ⁴ + registro|c|

|v ⁴ + 6v ² + 1| = |c/x ⁴ |

(y ⁴ + 6x ² y ² + x ⁴ ) = c

En y = 1, x = 1

(1 + 6 + 1) = c

c = 8

(y ⁴ + 6x ² y ² + x ⁴ ) = 8

Pregunta 36 (viii). {xsen ² (y/x) – y}dx + xdy = 0, y(1) = π/4

Solución:

Tenemos,

{xsen ² (y/x) – y}dx + xdy = 0

dy/dx = [y – xsen ² (y/x)]/x

dy/dx = (y/x) – sen ² (y/x)

es una ecuacion homogenea

Entonces, pon y = vx (i)

dy/dx = v + x(dv/dx)

Asi que,

v + x(dv/dx) = v – sen ² (v)

x(dv/dx) = v – sen ² (v) – v

x(dv/dx) = -sen ² (v)

-coseg ² (v)dv = (dx/x)

Al integrar ambos lados,

-∫coseg ² (v) = ∫(dx/x)

cuna(v) = log|x| + log|c|

cuna(y/x) = log|xc|

En x = 1, y = π/4

cuna(π/4) = log|c|

registro|c| = 1

c = mi

cuna(y/x) = log|ex|

Pregunta 36(ix). x(dy/dx) – y + xsen(y/x) = 0, y(2) = π

Solución:

Tenemos,

x(dy/dx) – y + xsen(y/x) = 0

x(dy/dx) = y – xsen(y/x)

(dy/dx) = (y/x) – sin(y/x)

es una ecuacion homogenea

Entonces, pon y = vx (i)

dy/dx = v + x(dv/dx)

Asi que,

v + x(dv/dx) = v – sen(v)

x(dv/dx) = v – sin(v) – v

x(dv/dx) = -sen(v)

-cosec(v)dv = (dx/x)

Al integrar ambos lados,

∫coseg(v) = -∫(dx/x)

log|cosec(v) – cot(v)| = -log|x| + log|c|

log|cosec(v) – cot(v)| = -log|x| + log|c|

log|cosec(y/x) – cot(y/x)| = -log|x| + log|c|

En x = 2, y = π

|cosec(π/2) – cot(π/2)| = -registro|2| + log|c|

registro|c| = 0

log|cosec(y/x) – cot(y/x)| = -log|x|

Pregunta 37. xcos(y/x)(dy/dx) = ycos(y/x) + x, Cuando x = 1, y = π/4

Solución:

Tenemos,

xcos(y/x)(dy/dx) = ycos(y/x) + x

$\frac{dy}{dx}=\frac{ycos(\frac{y}{x})+x}{xcos(\frac{y}{x})}$

(dy/dx) = (y/x) + [1/cos(y/x)]

Entonces, pon y = vx (i)

dy/dx = v + x(dv/dx)

Asi que,

v + x(dv/dx) = v + 1/cosv

x(dv/dx) = v + 1/cosv – v

x(dv/dx) = 1/cosv

cosvdv = (dx/x)

Al integrar ambos lados,

∫cosvdv = ∫(dx/x)

sen(v) = log|x| + log|c|

sin(y/x) = log|x| + log|c|

En x = 1, y = π/4

1/√2 = 0 + log|c|

registro|c| = (1/√2)

sin(y/x) = log|x| + (1/√2)

Pregunta 38. (x – y)(dy/dx) = (x + 2y), cuando x = 1,y = 0

Solución:

Tenemos,

(x – y)(dy/dx) = (x + 2y)

(dy/dx) = (x + 2y)/(x – y)

es una ecuacion homogenea

Entonces, pon y = vx (i)

dy/dx = v + x(dv/dx)

Asi que,

v + x(dv/dx) = (x + 2vx)/(x – vx)

v + x(dv/dx) = (1 + 2v)/(1 – v)

x(dv/dx) = [(1 + 2v)/(1 – v)] – v

x(dv/dx) = (1 + 2v – v + v ² )/(1 – v)

(1 – v)dv/(1 + v + v ² ) = (dx/x)

Al integrar ambos lados,

$∫\frac{1-v}{1+v+v^2}dv=\frac{dx}{x}$

$\frac{1}{2}∫\frac{2-2v}{1+v+v^2}dv=∫\frac{dx}{x}$

$∫\frac{3-(1+2v)}{1+v+v^2}dv=∫\frac{dx}{x}$

$\frac{3}{2}∫\frac{dv}{1+v+v^2}-\frac{1}{2}∫\frac{2v+1}{1+v+v^2}dv=∫\frac{dx}{x}$

$\frac{3}{2}∫\frac{dv}{(v+\frac{1}{2})^2+(\frac{\sqrt{3}}{2})^2}-\frac{1}{2}log|v^2+v+1|=log|x|+c$

$\sqrt{3}tan^{-1}(\frac{v+\frac{1}{2}}{\frac{\sqrt{3}}{2}})-\frac{1}{2}log|v^2+v+1|=log|x|+c$

$\sqrt{3}tan^{-1}(\frac{2y+1}{\sqrt{3}x})-\frac{1}{2}log|\frac{x^2+xy+y^2}{x^2}|=log|x|+c$

$\sqrt{3}tan^{-1}(\frac{2y+1}{\sqrt{3}x})-\frac{1}{2}log|x^2+xy+y^2|+log|x|=log|x|+c$

$\sqrt{3}tan^{-1}(\frac{2y+1}{\sqrt{3}x})-\frac{1}{2}log|x^2+xy+y^2|=c$

En x = 1, y = 0

√3tan ^-1 |1/√3| – (1/2)registro|1| = do

c = √3(π/6)

c = (π/2√3)

$\sqrt{3}tan^{-1}(\frac{2y+1}{\sqrt{3}x})-\frac{1}{2}log|x^2+xy+y^2|=\frac{π}{2\sqrt{3}}$

$\frac{1}{2}log|x^2+xy+y^2|=2\sqrt{3}tan^{-1}(\frac{2y+1}{\sqrt{3}x})-\frac{π}{\sqrt{3}}$

Pregunta 39. (dy/dx) = xy/(x ² + y ² )

Solución:

Tenemos,

(dy/dx) = xy/(x ² + y ² )

es una ecuacion homogenea

Entonces, pon y = vx (i)

dy/dx = v + x(dv/dx)

Asi que,

v + x(dv/dx) = xvx/(x ² + v ² x ² )

v + x(dv/dx) = v/(1 + ^v2 )

x(dv/dx) = [v/(1 + v2 ⁾ ] – v

x(dv/dx) = (v – v – v ³ )/(1 + v ² )

[-(1/v ³ ) – (1/v)]dv = (dx/x)

Al integrar ambos lados,

-∫dv/v ³ – ∫dv/v = ∫(dx/x)

(1/2v ² ) – log|v| = registro|x| +c

(x2 /2y2 ⁾⁼ log|vx| +c

(x ² /2y ² ) = log|(y/x)x| +c

(x ² /2y ² ) = log|y| +c

En x = 0, y = 1

c = 0

(x ² /2y ² ) = log|y|

Publicación traducida automáticamente

Artículo escrito por vivekray59 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 12 Soluciones RD Sharma – Capítulo 22 Ecuaciones diferenciales – Ejercicio 22.9 | conjunto 3

Pregunta 27. (x ² – 2xy)dy + (x ² – 3xy + 2y ² )dx = 0

Pregunta 28. x(dy/dx) = y – xcos ² (y/x)

Pregunta 29. x(dy/dx) – y = 2√(y ² – x ² )

Pregunta 30. xcos(y/x)(ydx + xdy) = ysen(y/x)(xdy – ydx)

Pregunta 31. (x ² + 3xy + y ² )dx – x ² dy = 0

Pregunta 32. (x – y)(dy/dx) = (x + 2y)

Pregunta 33. (2x ² y + y ³ )dx + (xy ² – 3x ² )dy = 0

Pregunta 34. x(dy/dx) – y + xsen(y/x) = 0

Pregunta 35. ydx + {xlog(y/x)}dy – 2xydy = 0

Pregunta 36(i). (x2 + ^{y2 )dx}⁼ 2xydy, y(1) = 0

Pregunta 36(ii). xe ^x/y – y + x(dy/dx) = 0, y(e) = 0

Pregunta 36(iii). (dy/dx) – (y/x) + cosec(y/x) = 0, y(1) = 0

Pregunta 36(iv). (xy – y ² )dx – x ² dy = 0, y(1) = 1

Pregunta 36(v). (dy/dx) = [y(x + 2y)]/[x(2x + y)]

Pregunta 36 (vi). (y ⁴ – 2x ³ y)dx + (x ⁴ – 2xy ³ )dy = 0, y(1) = 0

Pregunta 36 (vii). x(x ² + 3y ² )dx + y(y ² + 3x ² )dy = 0, y(1) = 1

Pregunta 36 (viii). {xsen ² (y/x) – y}dx + xdy = 0, y(1) = π/4

Pregunta 36(ix). x(dy/dx) – y + xsen(y/x) = 0, y(2) = π

Pregunta 37. xcos(y/x)(dy/dx) = ycos(y/x) + x, Cuando x = 1, y = π/4

Pregunta 38. (x – y)(dy/dx) = (x + 2y), cuando x = 1,y = 0

Pregunta 39. (dy/dx) = xy/(x ² + y ² )

Deja una respuesta Cancelar la respuesta

Pregunta 27. (x 2 – 2xy)dy + (x 2 – 3xy + 2y 2 )dx = 0

Pregunta 28. x(dy/dx) = y – xcos 2 (y/x)

Pregunta 29. x(dy/dx) – y = 2√(y 2 – x 2 )

Pregunta 30. xcos(y/x)(ydx + xdy) = ysen(y/x)(xdy – ydx)

Pregunta 31. (x 2 + 3xy + y 2 )dx – x 2 dy = 0

Pregunta 32. (x – y)(dy/dx) = (x + 2y)

Pregunta 33. (2x 2 y + y 3 )dx + (xy 2 – 3x 2 )dy = 0

Pregunta 34. x(dy/dx) – y + xsen(y/x) = 0

Pregunta 35. ydx + {xlog(y/x)}dy – 2xydy = 0

Pregunta 36(i). (x2 + y2 )dx = 2xydy, y(1) = 0

Pregunta 36(ii). xe x/y – y + x(dy/dx) = 0, y(e) = 0

Pregunta 36(iii). (dy/dx) – (y/x) + cosec(y/x) = 0, y(1) = 0

Pregunta 36(iv). (xy – y 2 )dx – x 2 dy = 0, y(1) = 1

Pregunta 36(v). (dy/dx) = [y(x + 2y)]/[x(2x + y)]

Pregunta 36 (vi). (y 4 – 2x 3 y)dx + (x 4 – 2xy 3 )dy = 0, y(1) = 0

Pregunta 36 (vii). x(x 2 + 3y 2 )dx + y(y 2 + 3x 2 )dy = 0, y(1) = 1

Pregunta 36 (viii). {xsen 2 (y/x) – y}dx + xdy = 0, y(1) = π/4

Pregunta 36(ix). x(dy/dx) – y + xsen(y/x) = 0, y(2) = π

Pregunta 37. xcos(y/x)(dy/dx) = ycos(y/x) + x, Cuando x = 1, y = π/4

Pregunta 38. (x – y)(dy/dx) = (x + 2y), cuando x = 1,y = 0

Pregunta 39. (dy/dx) = xy/(x 2 + y 2 )

Deja una respuesta Cancelar la respuesta

Pregunta 27. (x ² – 2xy)dy + (x ² – 3xy + 2y ² )dx = 0

Pregunta 28. x(dy/dx) = y – xcos ² (y/x)

Pregunta 29. x(dy/dx) – y = 2√(y ² – x ² )

Pregunta 31. (x ² + 3xy + y ² )dx – x ² dy = 0

Pregunta 33. (2x ² y + y ³ )dx + (xy ² – 3x ² )dy = 0

Pregunta 36(i). (x2 + ^{y2 )dx}⁼ 2xydy, y(1) = 0

Pregunta 36(ii). xe ^x/y – y + x(dy/dx) = 0, y(e) = 0

Pregunta 36(iv). (xy – y ² )dx – x ² dy = 0, y(1) = 1

Pregunta 36 (vi). (y ⁴ – 2x ³ y)dx + (x ⁴ – 2xy ³ )dy = 0, y(1) = 0

Pregunta 36 (vii). x(x ² + 3y ² )dx + y(y ² + 3x ² )dy = 0, y(1) = 1

Pregunta 36 (viii). {xsen ² (y/x) – y}dx + xdy = 0, y(1) = π/4

Pregunta 39. (dy/dx) = xy/(x ² + y ² )