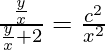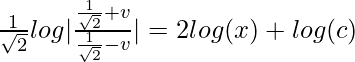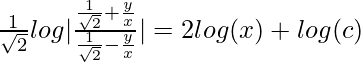Clase 12 Soluciones RD Sharma – Capítulo 22 Ecuaciones diferenciales – Ejercicio 22.9

Resuelve las siguientes ecuaciones diferenciales:

Pregunta 1. x ² dy + y(x + y)dy = 0

Solución:

Tenemos,

x ² dy + y(x + y)dy = 0

dy/dx = -y(x + y)/x ²

es una ecuacion homogenea

Entonces, pon y = vx (i)

Al diferenciar ambos lados de x,

dy/dx = v + x(dv/dx)

Asi que,

v + x(dv/dx) = -vx(x + vx)/x ²

v + x(dv/dx) = -v – ^v2

^{x(dv/dx) =} -2v – v2

$\frac{dv}{(v^2 + 2v)} = -\frac{dx}{x}$

Al integrar ambos lados,

$∫\frac{dv}{(v^2+2v+1-1)}=-∫(\frac{dx}{x})$

$∫\frac{dv}{(v+1)^2-(1)^2}=-log(x)$

$\frac{1}{2}log(\frac{v+1-1}{v+1+1})=-log|x|+log|c|$

log|v/(v + 2)| ^1/2 = -log|x/c|

v/(v + 2) = c ² /x ²

$\frac{\frac{y}{x}}{\frac{y}{x}+2}=\frac{c^2}{x^2}$

yx ² = (y + 2x)c ² (Donde ‘c’ es la constante de integración)

Pregunta 2. (dy/dx) = (y – x)/(y + x)

Solución:

Tenemos,

(dy/dx) = (y – x)/(y + x)

es una ecuacion homogenea

Entonces, pon y = vx (i)

Al diferenciar ambos lados de x,

dy/dx = v + x(dv/dx)

Asi que,

v + x(dv/dx) = (vx – x)/(vx + x)

v + x(dv/dx) = (v – 1)/(v + 1)

x(dv/dx) = (v – 1)/(v + 1) – v

x(dv/dx) = (v – 1 – v ² – v)/(v + 1)

x(dv/dx) = -(v ² + 1)/(v + 1)

$\frac{(v+1)dv}{(v^2+1)}=-\frac{dx}{x}$

Al integrar ambos lados,

$∫\frac{(v+1)dv}{(v^2+1)}=-∫\frac{dx}{x}$

∫vdv/(v ² +1)+∫dv/(v ² +1)=-∫(dx/x)

$\frac{1}{2}∫\frac{2v}{v^2+1}+∫\frac{dv}{v^2+1}=-log|x|+log|c|$

(1/2)log|v ² + 1| + tan ^-1 (v) = log(c/x)

log|(y ² + x ² )/x ² | + 2tan ^-1 (y/x) = log(c/x) ²

log(y ² + x ² ) – log(x) ² + 2tan ^-1 (y/x) = log(c/x) ²

log(y ² + x ² ) + 2tan ^-1 (y/x) = 2log(c) (Donde ‘c’ es la constante de integración)

Pregunta 3. (dy/dx) = (y ² – x ² )/2yx

Solución:

Tenemos,

(dy/dx) = (y ² – x ² )/2yx

es una ecuacion homogenea

Entonces, pon y = vx (i)

Al diferenciar ambos lados de x,

dy/dx = v + x(dv/dx)

Asi que,

v + x(dv/dx) = (v ² x ² – x ² )/2vx ²

v + x(dv/dx) = (v ² – 1)/2v

x(dv/dx) = [(v ² – 1)/2v] – v

x(dv/dx) = (v ² – 1 – 2v ² )/2v

x(dv/dx) = -(v ² + 1)/2v

$\frac{2vdv}{(v^2 + 1)} = -\frac{dx}{x}$

Al integrar ambos lados,

$∫\frac{vdv}{(v^2+1)}=-∫\frac{dx}{x}$

registro|v ² +1| = -log(x) + log(c)

registro|v ² +1| = registro(c/x)

y ² /x ² + 1 = |c/x|

(x ² + y ² ) = cx (Donde ‘c’ es la constante de integración)

Pregunta 4. x(dy/dx) = (x + y)

Solución:

Tenemos,

x(dy/dx) = (x+y)

(dy/dx) = (x+y)/x

es una ecuacion homogenea

Entonces, pon y = vx (i)

Al diferenciar ambos lados de x,

dy/dx = v + x(dv/dx)

Asi que,

v + x(dv/dx) = (x + vx)/x

v + x(dv/dx) = (1 + v)

x(dv/dx) = 1

dv = (dx/x)

Al integrar ambos lados,

∫dv = ∫(dx/x)

v = log(x) + c

y/x = log(x) + c

y = xlog(x) + cx (Donde ‘c’ es la constante de integración)

Pregunta 5. (x ² – y ² )dx – 2xydy = 0

Solución:

Tenemos,

(x ² – y ² )dx – 2xydy = 0

(dy/dx) = (x2 – ^y2 )/ ^2xy

es una ecuacion homogenea

Entonces, pon y = vx (i)

Al diferenciar ambos lados de x,

dy/dx = v + x(dv/dx)

Asi que,

v + x(dv/dx) = (x ² – v ² x ² )/2xvx

v + x(dv/dx) = (1 – v2 ⁾ /2v

x(dv/dx) = [(1 – v ² )/2v] – v

x(dv/dx) = (1 – 3v ² )/2v

$\frac{2vdv}{(1-3v^2)} = \frac{dx}{x}$

Al integrar ambos lados,

$∫\frac{2vdv}{(1-3v^2)}=∫\frac{dx}{x}$

$\frac{1}{3}∫\frac{6v}{1-3v^2}dv=∫\frac{dx}{x}$

-(1/3)log(1 – 3v ² ) = log(x) – log(c)

log(1 – 3v ² ) = -log(x) ³ + log(c)

$(1-\frac{3y^2}{x^2})=(\frac{c}{x^3})$

(x ² – 3y ² )/x ² = (c/x ³ )

x(x ² – 3y ² ) = c (Donde ‘c’ es la constante de integración)

Pregunta 6. (dy/dx) = (x + y)/(x – y)

Solución:

Tenemos,

(dy/dx) = (x + y)/(x – y)

es una ecuacion homogenea

Entonces, pon y = vx (i)

Al diferenciar ambos lados de x,

dy/dx = v + x(dv/dx)

Asi que,

v + x(dv/dx) = (x + vx)/(x – vx)

v + x(dv/dx) = (1 + v)/(1 – v)

x(dv/dx) = [(1 + v)/(1 – v)] – v

x(dv/dx) = (1 + v – v + v ² )/(1 – v)

x(dv/dx) = (1 + v ² )/(1 – v)

$\frac{(1-v)dv}{(v^2+1)}=\frac{dx}{x}$

Al integrar ambos lados,

$∫\frac{(v+1)dv}{(v^2+1)}=∫\frac{dx}{x}$

∫dv/(v ² + 1) – ∫vdv/(v ² + 1) = ∫(dx/x)

tan ^-1 (v) – (1/2)log(v ² + 1) = log(x) + c

tan ^-1 (y/x) – (1/2)log(y ² /x ² + 1) = log(x) + c

tan ^-1 (y/x) – (1/2)log(y ² + x ² ) + log(x) = log(x) + c

tan ^-1 (y/x) = (1/2)log(y ² + x ² ) + c (Donde ‘c’ es la constante de integración)

Pregunta 7. 2xy(dy/dx) = (x ² + y ² )

Solución:

Tenemos,

^2xy (dy/dx) = (x2 + ^y2 )

(dy/dx) = (x2 + ^y2 )/ ^2xy

es una ecuacion homogenea

Entonces, pon y = vx (i)

Al diferenciar ambos lados de x,

dy/dx = v + x(dv/dx)

Asi que,

v + x(dv/dx) = (x ² + v ² x ² )/2xvx

v + x(dv/dx) = (1 + v2 ⁾ /2v

x(dv/dx) = [(1 + v ² )/2v] – v

x(dv/dx) = (1 – v2 ⁾ /2v

$\frac{2vdv}{(1 - v^2)} = \frac{dx}{x}$

Al integrar ambos lados,

$∫\frac{2vdv}{(1 - v^2)} = ∫\frac{dx}{x}$

-log(1 – v ² ) = log(x) – log(c)

log(1 – v ² ) = -log(x) + log(c)

1 – y2 ^/ x2 ⁼ (c/x)

(x ² – y ² ) = cx (Donde ‘c’ es la constante de integración)

Pregunta 8. x ² (dy/dx) = x ² – 2y ² + xy

Solución:

Tenemos,

x2 (dy/dx) = x2 – ^2y2⁺^xy

(dy/dx) = (x2 ^– 2y2 ⁺ xy)/ ^x2

es una ecuacion homogenea

Entonces, pon y = vx (i)

Al diferenciar ambos lados de x,

dy/dx = v + x(dv/dx)

Asi que,

v + x(dv/dx) = (x ² – 2v ² x ² + xvx)/2xvx

v + x(dv/dx) = (1 – 2v ² + v)/x ²

x(dv/dx) = (1 – 2v ² + v) – v

x(dv/dx) = (1 – 2v ² )

dv/(1 – 2v ² ) = (dx/x)

Al integrar ambos lados,

dv/(1 – 2v ² ) = ∫(dx/x)

$∫\frac{dv}{v^2-\frac{1}{2}}=-2\frac{dx}{x}$

$∫\frac{dv}{(\frac{1}{\sqrt2})^2-v^2}=2\frac{dx}{x}$

$\frac{1}{\sqrt{2}}log|\frac{\frac{1}{\sqrt{2}}+v}{\frac{1}{\sqrt{2}}-v}|=2log(x)+log(c)$

$\frac{1}{\sqrt{2}}log|\frac{\frac{1}{\sqrt{2}}+\frac{y}{x}}{\frac{1}{\sqrt{2}}-\frac{y}{x}}|=2log(x)+log(c)$

$(\frac{1}{√2})log|\frac{(x + y√2)}{(x - y√2)}|=log(x)^2 + log(c)$

$|\frac{(x + y√2)}{(x - y√2)}|^{\frac{1}{√2}} = cx^2$

$|\frac{(x+y√2)}{(x-y√2)}|=|cx^2|^{√2}$ (Donde ‘c’ es constante de integración)

Pregunta 9. xy(dy/dx) = x ² – y ²

Solución:

Tenemos,

xy(dy/dx) = ^x2 – ^y2

(dy/dx) = (x ² – y ² )/xy

es una ecuacion homogenea

Entonces, pon y = vx (i)

Al diferenciar ambos lados de x,

dy/dx = v + x(dv/dx)

Asi que,

v + x(dv/dx) = (x ² – v ² x ² )/xvx

v + x(dv/dx) = (1 – v ² )/v

x(dv/dx) = [(1 – v ² )/v] – v

x(dv/dx) = (1 – 2v ² )/v

vdv/(1 – 2v ² ) = (dx/x)

Al integrar ambos lados,

∫vdv/(1 – 2v ² ) = ∫(dx/x)

∫4vdv/(1 – 2v ² ) = 4∫(dx/x)

-log(1 – 2v ² ) = 4log(x) – log(c)

log(1 – 2v ² ) = log(c/x ⁴ )

(1 – 2y ² /x ² ) = c/x ⁴

(x ² -2y ² )/x ² = c/x ⁴

x ² (x ² – 2y ² ) = c (Donde ‘c’ es la constante de integración)

Pregunta 10. ye ^x/y dx = (xe ^x/y + y)dy

Solución:

Tenemos,

ye ^x/y dx = (xe ^x/y + y)dy

(dy/dx) = (xe ^x/y + y)/ye ^x/y

es una ecuacion homogenea

Entonces, pon x = vy (i)

Al diferenciar ambos lados de x,

dx/dy = v + y(dv/dy)

Asi que,

v + y(dv/dy) = (vye ^vy/y + y)/ye ^vy/y

v + y(dv/dy) = (ve ^v + 1)/e ^v

y(dv/dy) = [(ve ^v + 1)/e ^v ] – v

y(dv/dy) = (ve ^v + 1 – ve ^v )/e ^v

y(dv/dy) = (1/e ^v )

e ^v dv = (dy/y)

Al integrar ambos lados,

∫e ^v dv = ∫(dy/y)

e ^v = log(y) + log(c)

e ^x/y = log(y) + log(c) (Donde ‘c’ es la constante de integración)

Pregunta 11. x ² (dy/dx) = x ² + xy + y ²

Solución:

Tenemos,

x ² (dy/dx) = x ² + xy + y ²

dy/dx = (x2 ⁺ xy + y2 ⁾^/ x2

es una ecuacion homogenea

Entonces, pon y = vx (i)

Al diferenciar ambos lados de x,

dy/dx = v + x(dv/dx)

Asi que,

v + x(dv/dx) = (x ² + xvx + v ² x ² )/x ²

v + x(dv/dx) = (1 + v + v ² )

x(dv/dx) = (1 + v + v ² ) – v

dv/(1 + v ² ) = (dx/x)

Al integrar ambos lados,

∫dv/(1 + v ² ) = ∫(dx/x)

bronceado ^-1 (v) = log|x| +c

tan ^-1 (y/x) = log|x| + c (Donde ‘c’ es constante de integración)

Pregunta 12. (y ² – 2xy)dx = (x ² – 2xy)dy

Solución:

Tenemos,

( ^y2 – 2xy)dx = (x2 – ^2xy )dy

(dy/dx) = ( ^y2 – 2xy)/(x2 – ^2xy )

es una ecuacion homogenea

Entonces, pon y = vx (i)

Al diferenciar ambos lados de x,

dy/dx = v + x(dv/dx)

Asi que,

v + x(dv/dx) = (v ² x ² – 2xvx)/(x ² – 2xvx)

v + x(dv/dx) = ( ^v2 – 2v)/(1 – 2v)

x(dv/dx) = [(v ² – 2v – v + 2v ² )/(1 – 2v)]

x(dv/dx) = 3(v ² – 1)/(1 – 2v)

-(2v – 1)dv/(v ² – v) = 3(dx/x)

Al integrar ambos lados,

-∫(2v – 1)dv/(v ² – v) = 3∫(dx/x)

-registro|v ² – v| = 3log|x| – registro|c|

registro|v ² – v| = registro|c/x ³ |

(y2 ^/ x2 – y/x) = (c ^/^x3 )

(y ² – xy) = c/x

x(y ² – xy) = c (Donde ‘c’ es la constante de integración)

Pregunta 13. 2xydx + (x ² + 2y ² )dy = 0

Solución:

Tenemos,

2xydx + (x ² + 2y ² )dy = 0

dy/dx = -(2xy)/(x ² + 2y ² )

es una ecuacion homogenea

Entonces, pon y = vx (i)

Al diferenciar ambos lados de x,

dy/dx = v + x(dv/dx)

Asi que,

v + x(dv/dx) = -(2xvx)/(x ² + 2v ² x ² )

v + x(dv/dx) = -(2v)/(1 + 2v ² )

x(dv/dx) = -[(2v)/(1 + 2v ² )] – v

$x\frac{dv}{dx}=\frac{-3v-2v^3}{1+2v^2}$

$\frac{1+2v^2}{3v+2v^3}dv=-\frac{dx}{x}$

Al integrar ambos lados,

$∫\frac{1+2v^2}{3v+2v^3}dv=-∫\frac{dx}{x}$

Sustituyendo (3v + 2v ³ ) = z

Al diferenciar ambos lados de x,

3(1 + 2v)dv = dz

(1 + 2v)dv = (dz/3)

(1/3)∫(dz/z) = -∫(dx/x)

(1/3)log|z| = -log|x| + log|c|

registro|3v + 2v ³ | = registro|c/x| ³

3y/x + 2(y/x) ³ = (c/x) ³

(3yx ² + 2y ³ ) = c (Donde ‘c’ es la constante de integración)

Publicación traducida automáticamente

Artículo escrito por vivekray59 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 12 Soluciones RD Sharma – Capítulo 22 Ecuaciones diferenciales – Ejercicio 22.9 | Serie 1

Resuelve las siguientes ecuaciones diferenciales:

Pregunta 1. x ² dy + y(x + y)dy = 0

Pregunta 2. (dy/dx) = (y – x)/(y + x)

Pregunta 3. (dy/dx) = (y ² – x ² )/2yx

Pregunta 4. x(dy/dx) = (x + y)

Pregunta 5. (x ² – y ² )dx – 2xydy = 0

Pregunta 6. (dy/dx) = (x + y)/(x – y)

Pregunta 7. 2xy(dy/dx) = (x ² + y ² )

Pregunta 8. x ² (dy/dx) = x ² – 2y ² + xy

Pregunta 9. xy(dy/dx) = x ² – y ²

Pregunta 10. ye ^x/y dx = (xe ^x/y + y)dy

Pregunta 11. x ² (dy/dx) = x ² + xy + y ²

Pregunta 12. (y ² – 2xy)dx = (x ² – 2xy)dy

Pregunta 13. 2xydx + (x ² + 2y ² )dy = 0

Deja una respuesta Cancelar la respuesta

Resuelve las siguientes ecuaciones diferenciales:

Pregunta 1. x 2 dy + y(x + y)dy = 0

Pregunta 2. (dy/dx) = (y – x)/(y + x)

Pregunta 3. (dy/dx) = (y 2 – x 2 )/2yx

Pregunta 4. x(dy/dx) = (x + y)

Pregunta 5. (x 2 – y 2 )dx – 2xydy = 0

Pregunta 6. (dy/dx) = (x + y)/(x – y)

Pregunta 7. 2xy(dy/dx) = (x 2 + y 2 )

Pregunta 8. x 2 (dy/dx) = x 2 – 2y 2 + xy

Pregunta 9. xy(dy/dx) = x 2 – y 2

Pregunta 10. ye x/y dx = (xe x/y + y)dy

Pregunta 11. x 2 (dy/dx) = x 2 + xy + y 2

Pregunta 12. (y 2 – 2xy)dx = (x 2 – 2xy)dy

Pregunta 13. 2xydx + (x 2 + 2y 2 )dy = 0

Deja una respuesta Cancelar la respuesta

Pregunta 1. x ² dy + y(x + y)dy = 0

Pregunta 3. (dy/dx) = (y ² – x ² )/2yx

Pregunta 5. (x ² – y ² )dx – 2xydy = 0

Pregunta 7. 2xy(dy/dx) = (x ² + y ² )

Pregunta 8. x ² (dy/dx) = x ² – 2y ² + xy

Pregunta 9. xy(dy/dx) = x ² – y ²

Pregunta 10. ye ^x/y dx = (xe ^x/y + y)dy

Pregunta 11. x ² (dy/dx) = x ² + xy + y ²

Pregunta 12. (y ² – 2xy)dx = (x ² – 2xy)dy

Pregunta 13. 2xydx + (x ² + 2y ² )dy = 0