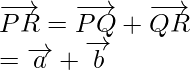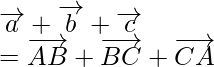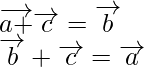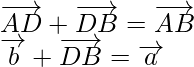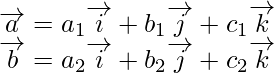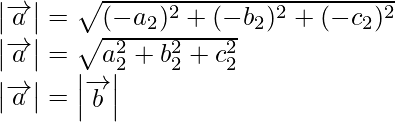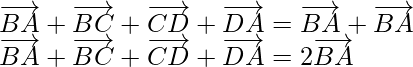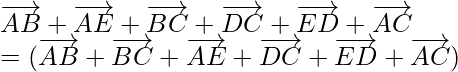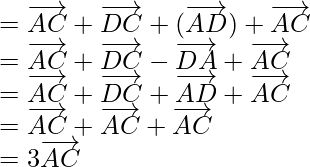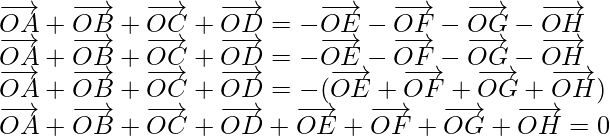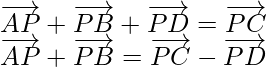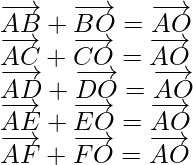Pregunta 1. Si P, Q y R son tres puntos colineales tales que 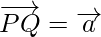 y
y 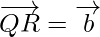 . Encuentra el vector
. Encuentra el vector 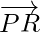
Solución:
Según la pregunta, dado que
Los puntos P, Q y R son colineales.
También,
y
Asi que,
Pregunta 2. Dada la condición de que tres vectores 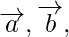 y
y 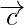 forman los tres lados de un triángulo. ¿Cuáles son otras posibilidades?
forman los tres lados de un triángulo. ¿Cuáles son otras posibilidades?
Solución:
Según la pregunta, dado que
son tres lados de un triángulo ABC.
[desde
]
[desde
]
Asi que,
Como sabemos que si los vectores están representados en magnitud y dirección por los dos lados
del triángulo tomado es del mismo orden, entonces su suma está representada por el tercer lado tomado en orden inverso.
Asi que,
o
Pregunta 3. Si 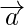 y
y 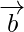 son dos vectores no colineales que tienen el mismo punto inicial. ¿Cuáles son los vectores representados por
son dos vectores no colineales que tienen el mismo punto inicial. ¿Cuáles son los vectores representados por 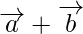 y
y 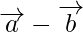 ?
?
Solución:
Según la pregunta, dado que
y
son dos vectores no colineales que tienen el mismo punto inicial.
Entonces, consideremos
Ahora dibujamos un paralelogramo llamado ABCD
Usando las propiedades del paralelogramo, obtenemos
En ∆ABC,
Usando la ley del triángulo, obtenemos
…….(i)
En ∆ABD,
Usando la ley del triángulo, obtenemos
…….(ii)
Al resolver las ecuaciones (i) y (ii), obtenemos
y
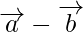
son las diagonales de un paralelogramo cuyos lados adyacentes son
y
Pregunta 4. Si 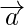 es un vector y m es un escalar tal que
es un vector y m es un escalar tal que 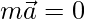 , ¿cuáles son las alternativas para m y
, ¿cuáles son las alternativas para m y 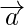 ?
?
Solución:
De acuerdo con la pregunta, dado que m es un escalar y
es un vector tal que
[desde que
]
Ahora, al comparar los coeficientes
de LHS y RHS, obtenemos
ma 1 = 0 ⇒ m = 0 o a 1 = 0 …….(i)
mb 1 = 0 ⇒ m = 0 o b 1 = 0 …….(ii)
mc 1 = 0 ⇒ m = 0 o c 1 = 0 …….(iii)
Ahora de la ecuación (i), (ii) y (iii), obtenemos
m = 0 o un 1 = segundo 1 = do 1 = 0
m = 0 o
m = 0 o
Pregunta 5. Si 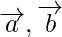 son dos vectores, entonces escribe el valor de verdad del siguiente enunciado:
son dos vectores, entonces escribe el valor de verdad del siguiente enunciado:
(yo) 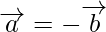 ⇒
⇒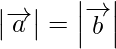
(ii)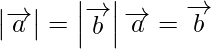
(iii)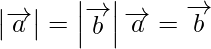
Solución:
(i) Supongamos
Dado que, a = -b
Asi que,
Ahora al comparar los coeficientes de i, j, k en LHS y RHS, obtenemos
a1 = a2 …….(yo)
b1 = b2 …….(ii)
c1 = c2 …….(iii)
De la ecuación (i), (ii) y (iii),
(ii) Dados a y b son dos vectores tales que
Entonces, significa que la magnitud del vector
es igual a la magnitud
del vector
, pero no podemos encontrar la dirección del vector.
Por lo tanto, es falso que
(iii) Dado para cualquier vector
son iguales pero no podemos encontrar la dirección del vector de
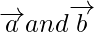
Entonces, es falso.
Pregunta 6. ABCD es un cuadrilátero. Encuentre la suma de los vectores 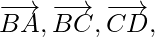 y
y 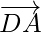 .
.
Solución:
Según la pregunta,
ABCD es un cuadrilátero.
asi que,
En ∆CAD,
Usando la ley del triángulo, obtenemos
……(i)
En ∆ABC,
Usando la ley del triángulo, obtenemos
……(ii)
Ahora pon el valor de
en la ecuación (ii), obtenemos
Ahora, al agregar
en ambos lados,
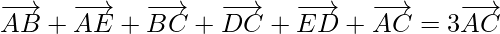
Pregunta 7. ABCDE es un pentágono, prueba que
(i)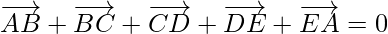
(ii)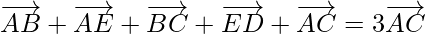
Solución:
(i) Según la pregunta,
ABCDE es un pentágono,
Asi que,
Usando la ley del triángulo
, obtenemos
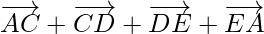
Usando la ley del triángulo
, obtenemos
= 0
Por lo tanto probado
(ii) Según la pregunta,
ABCDE es un pentágono,
Asi que,
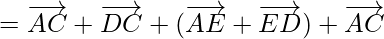
Usando la ley del triángulo
, obtenemos
Por lo tanto probado
Pregunta 8. Demuestra que la suma de todos los vectores dibujados desde el centro de un octágono regular hasta sus vértices es el vector cero.
Solución:
Supongamos que O es el centro de un octágono regular, ya que sabemos que el
El centro de un octágono regular biseca todas las diagonales que lo atraviesan.
Asi que,
…….(i)
…….(ii)
…….(iii)
[Tex]\overrightarrow{OD}=-\overrightarrow{OH} [/Tex] …….(iv)
Ahora, al sumar las ecuaciones (i), (ii) y (iv), obtenemos
Por lo tanto probado
Pregunta 9. Si P es un punto y ABCD es un cuadrilátero 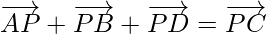 y, demuestra que ABCD es un paralelogramo.
y, demuestra que ABCD es un paralelogramo.
Solución:
Según la pregunta

Ya que,
Usando la ley del triángulo en ∆APB,
y usando la ley del triángulo en ∆ DPC,
Obtenemos
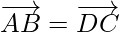
Entonces, AB es paralelo a DC e igual es la magnitud.
Por lo tanto, ABCD es un paralelogramo.
Pregunta 10. Cinco fuerzas 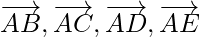 y
y 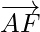 actúan en el vértice de un hexágono regular ABCDEF. Demostrar que la resultante es 6
actúan en el vértice de un hexágono regular ABCDEF. Demostrar que la resultante es 6 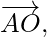 donde o es el centro del hexágono.
donde o es el centro del hexágono.
Solución:
Según la pregunta,
Pruebalo
Prueba:
Como sabemos que el centro (O) del hexágono biseca la diagonal
Asi que,
Ahora,
Al sumar estas ecuaciones, obtenemos
⇒
Pero
Asi que,
Por lo tanto probado
Publicación traducida automáticamente
Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA