Clase 12 Soluciones RD Sharma – Capítulo 23 Álgebra de Vectores – Ejercicio 23.3

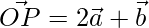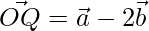Pregunta 1. Encuentra el vector de posición de un punto R que divide la línea que une los dos puntos P y Q con vectores de posición $\vec{OP}=2\vec{a}+\vec{b}$ y $\vec{OQ}=\vec{a}-2\vec{b}$ respectivamente en la proporción 1:2 interna y externamente.

Solución:

El punto R divide internamente la línea que une los puntos P y Q en la proporción 1:2.

El vector de posición de R = $\frac{\vec{a}-2\vec{b}+2(2\vec{a}+\vec{b})}{1+2}$ = $\frac{5\vec{a}}{3}$

El punto R divide exteriormente la línea que une P y Q en la proporción 1:2.

El vector de posición de R = $\frac{\vec{a}-2\vec{b}-2(2\vec{a}+\vec{b})}{1-2}$

= $\frac{-3\vec{a}-4\vec{b}}{-1}$

= $3\vec{a}+4\vec{b}$

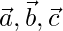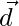Pregunta 2. Sean $\vec{a},\vec{b},\vec{c}$ y $\vec{d}$ los vectores de posición de los cuatro puntos distintos A, B, C, D. Si 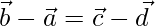$\vec{b}-\vec{a}=\vec{c}-\vec{d}$ entonces demuestre que ABCD es un paralelogramo.

Solución:

Dado que son los vectores de posición de los cuatro puntos distintos A, B, C, D

tal que $\vec{b}-\vec{a} = \vec{c}-\vec{d}$

Dado que,

$\vec{b}-\vec{a} = \vec{c}-\vec{d}$

$\vec{AB} = \vec{CD}$

Entonces, AB es paralelo e igual a DC

Por lo tanto, ABCD es un paralelogramo.

Pregunta 3.Si 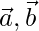$\vec{a},\vec{b}$ son los vectores de posición de A, B respectivamente, encuentre el vector de posición de un punto C en AB producido tal que AC = 3AB y que un punto D en BA producido tal que BD = 2BA.

Solución:

Dado que $\vec{a},\vec{b}$ son el vector de posición de A y B

Sea C un punto en AB producido tal que AC = 3AB.

De los datos dados podemos decir que el punto C divide a la línea AB en

Relación 3:2 externamente. Entonces, el vector de posición del punto C se puede escribir como

$\vec{c} = \frac{ m\vec{b}-n\vec{a}}{m-n}$

= $\frac{3\vec{b}-2\vec{a}}{3-2}$

= $3\vec{b}-2\vec{a}$

D sea un punto en BA producido tal que BD = 2BA

Está claro que el punto D divide la línea en 1:2 externamente.

Entonces el vector de posición $\vec{d}$ se puede escribir como

$\vec{d} = \frac{m\vec{a}-n{b}}{m-n}$

= $\frac{2\vec{a}-\vec{b}}{2-1}$

$\vec{d} = 2\vec{a}-\vec{b}$

Por lo tanto $\vec{c} =3\vec{b}-2\vec{a}$ y $\vec{d} = 2\vec{a}-\vec{b}$

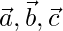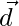Pregunta 4. Demuestra que los cuatro puntos A, B, C, D con vectores de posición $\vec{a},\vec{b},\vec{c}$ y $\vec{d}$ respectivamente tales que 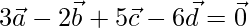$3\vec{a}-2\vec{b}+5\vec{c}-6\vec{d} =\vec{0}$ son coplanares. Además, encuentre el vector de posición del punto de intersección de las rectas AC y BD.

Solución:

Dado que $3\vec{a}-2\vec{b}+5\vec{c}-6\vec{d} =\vec{0}$

$3\vec{a}+5\vec{c} = 2\vec{b}+6\vec{d}$

La suma de los coeficientes en ambos lados de la ecuación dada es 8

Entonces, divide la ecuación por 8 en ambos lados.

$\frac{3\vec{a}+5\vec{c}}{8} = \frac{2\vec{b}+6\vec{d}}{8}$

$\frac{3\vec{a}+5\vec{c}}{3+5} = \frac{2\vec{b}+6\vec{d}}{2+6}$

Es claro que el vector de posición de un punto P que divide a Ac en el

La relación 3:5 es la misma que la del punto P buceando BD en la relación 2:6.

El punto P es común a AC y BD. Por lo tanto, P es el punto de intersección de AC y BD.

Por tanto, A, B, C y D son coplanares.

El vector de posición del punto P se puede escribir como

$\frac{3\vec{a}+5\vec{c}}{8}$ o $\frac{2\vec{b}+6\vec{d}}{8}$

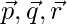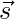Pregunta 5: Demostrar que los cuatro puntos P, Q, R, S con vectores de posición $\vec{p},\vec{q},\vec{r}$ y $\vec{s}$ respectivamente tales que 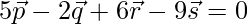$5\vec{p}-2\vec{q}+6\vec{r}-9\vec{s} = 0$ son coplanares. Además, encuentre el vector de posición del punto de intersección de las rectas PR y QS.

Solución:

Dado que $5\vec{p}-2\vec{q}+6\vec{r}-9\vec{s} = 0$

aquí $\vec{p}, \vec{q}, \vec{r},$ y $\vec{s}$

son los vectores de posición del punto P, Q, R, S

$5\vec{p}+6\vec{r} = 2\vec{q}+9\vec{s}$ -(1)

La suma de los coeficientes en ambos lados de la ecuación (1) es 11.

Entonces divide la ecuación (1) por 11 en ambos lados.

$\frac{5\vec{p}+6\vec{r}}{11} = \frac{2\vec{q}+9\vec{s}}{11}$

$\frac{5\vec{p}+6\vec{r}}{5+6} = \frac{2\vec{q}+9\vec{s}}{2+9}$

Muestra que el vector de posición de un punto A que divide a PR en la proporción de 6:5 y

QS en la proporción 9:2. Entonces A es el punto común de PR y QS.

Por tanto, P, Q, R y S son coplanares.

El vector de posición del punto A está dado por

$\frac{5\vec{p}+6\vec{q}}{11}$ o $\frac{2\vec{q}+9\vec{s}}{11}$

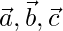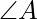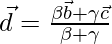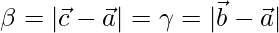Pregunta 6: Los vértices A, B, C del triángulo ABC tienen respectivamente vectores de posición $\vec{a},\vec{b},\vec{c}$ con respecto a un origen O dado. Muestre que el punto D donde la bisectriz de $\angle{A}$ BC se encuentra tiene un vector de posición $\vec{d}=\frac{\beta\vec{b}+\gamma\vec{c}}{\beta+\gamma}$ donde $\beta=|\vec{c}-\vec{a}| = \gamma=|\vec{b}-\vec{a}|$ . Por lo tanto, deducir que el incentro I tiene un vector de posición 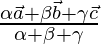$\frac{\alpha\vec{a}+\beta\vec{b}+\gamma\vec{c}}{\alpha+\beta+\gamma}$ donde $\alpha = |\vec{b}-\vec{c}|$

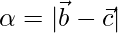
Solución:

Sea ABC un triángulo y los vectores de posición de A, B, C con respecto a algún origen sean O

Sea D el punto de BC donde se encuentra la bisectriz de $\angle{A}$ .

$\vec{d}$ Sea el vector de posición de D que divide internamente a BC en la razón $\beta$

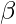
y $\gamma$ donde $\beta = |\vec{AC}| and \gamma = {\vec{b}-\vec{a}}$

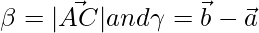
De este modo, $\beta=|\vec{c}-\vec{a}| and \gamma=|\vec{b}-\vec{a}|$

Por lo tanto, por fórmula de sección, el vector de posición de D viene dado por

$\vec{OD} = \frac{\beta\vec{b}+\gamma\vec{c}}{\beta+\gamma}$

Dejar $\alpha = |\vec{b}-\vec{c}|$

El incentro es el punto concurrente de las bisectrices de los ángulos.

Por lo tanto, Incentre divide la línea AD en la razón $\alpha:\beta+\gamma$ y

el vector de posición del incentro es igual a

$\frac{\alpha\vec{a}+\frac{\beta\vec{b}+\gamma\vec{c}}{(\beta+\gamma)}*(\beta+\gamma)}{\alpha+\beta+\gamma} = \frac{\alpha\vec{a}+\beta\vec{b}+\gamma\vec{c}}{\alpha+\beta+\gamma}$

Publicación traducida automáticamente

Artículo escrito por tejunallanukala y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Encuentra el vector de posición de un punto R que divide la línea que une los dos puntos P y Q con vectores de posición y respectivamente en la proporción 1:2 interna y externamente.

Pregunta 2. Sean y los vectores de posición de los cuatro puntos distintos A, B, C, D. Si entonces demuestre que ABCD es un paralelogramo.

Pregunta 3.Si son los vectores de posición de A, B respectivamente, encuentre el vector de posición de un punto C en AB producido tal que AC = 3AB y que un punto D en BA producido tal que BD = 2BA.

Pregunta 4. Demuestra que los cuatro puntos A, B, C, D con vectores de posición y respectivamente tales que son coplanares. Además, encuentre el vector de posición del punto de intersección de las rectas AC y BD.

Pregunta 5: Demostrar que los cuatro puntos P, Q, R, S con vectores de posición y respectivamente tales que son coplanares. Además, encuentre el vector de posición del punto de intersección de las rectas PR y QS.

Deja una respuesta Cancelar la respuesta

Pregunta 1. Encuentra el vector de posición de un punto R que divide la línea que une los dos puntos P y Q con vectores de posición $\vec{OP}=2\vec{a}+\vec{b}$ y $\vec{OQ}=\vec{a}-2\vec{b}$ respectivamente en la proporción 1:2 interna y externamente.

Pregunta 2. Sean $\vec{a},\vec{b},\vec{c}$ y $\vec{d}$ los vectores de posición de los cuatro puntos distintos A, B, C, D. Si $\vec{b}-\vec{a}=\vec{c}-\vec{d}$ entonces demuestre que ABCD es un paralelogramo.

Pregunta 3.Si $\vec{a},\vec{b}$ son los vectores de posición de A, B respectivamente, encuentre el vector de posición de un punto C en AB producido tal que AC = 3AB y que un punto D en BA producido tal que BD = 2BA.

Pregunta 4. Demuestra que los cuatro puntos A, B, C, D con vectores de posición $\vec{a},\vec{b},\vec{c}$ y $\vec{d}$ respectivamente tales que $3\vec{a}-2\vec{b}+5\vec{c}-6\vec{d} =\vec{0}$ son coplanares. Además, encuentre el vector de posición del punto de intersección de las rectas AC y BD.

Pregunta 5: Demostrar que los cuatro puntos P, Q, R, S con vectores de posición $\vec{p},\vec{q},\vec{r}$ y $\vec{s}$ respectivamente tales que $5\vec{p}-2\vec{q}+6\vec{r}-9\vec{s} = 0$ son coplanares. Además, encuentre el vector de posición del punto de intersección de las rectas PR y QS.