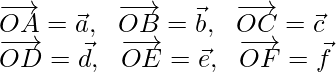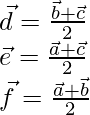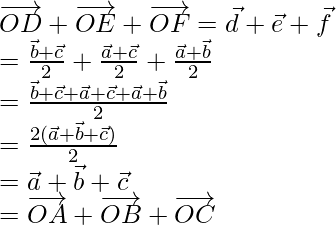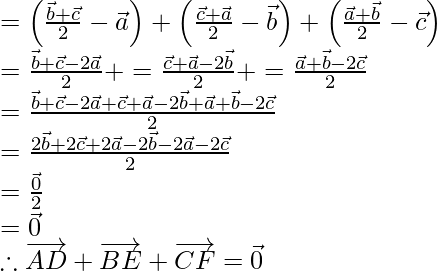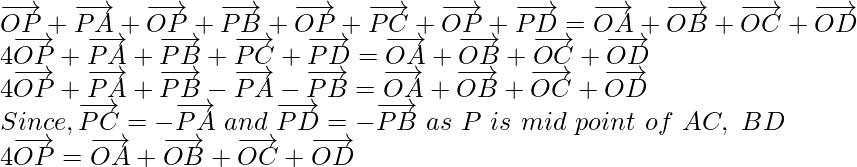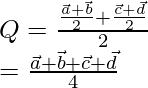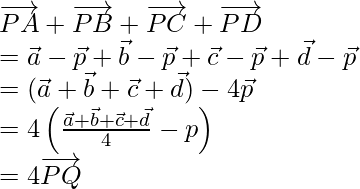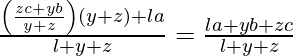Pregunta 1. Si O es un punto en el espacio, ABC es un triángulo y D, E, F son los puntos medios de los lados BC, CA y AB respectivamente del triángulo, demuestre que
Solución:

En el △ABC, D, E, F son los puntos medios de los lados de BC, CA y AB y O es cualquier punto del espacio.
Consideremos
el vector de posición del punto A, B, C, D, E, F con respecto a O.
Por lo tanto,
Entonces, de acuerdo con la fórmula del punto medio
Por lo tanto, demostrado
Pregunta 2. Muestre que la suma de tres vectores determinados por las medianas de un triángulo dirigido desde los vértices es cero.

Solución:
Consideremos que ABC es un triángulo, por lo que los vectores de posición de A, B y C son
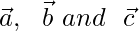
Por lo tanto, AD, BE, CF son medios, por lo tanto, D, E y F son puntos medios de la línea BC, AC y AB.
Ahora, usando la fórmula del punto medio obtenemos
Vector de posición de D =
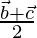
Vector de posición de E =
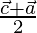
Vector de posición de F =
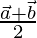
Ahora, suma las tres medianas
Por tanto, se demostró que la suma de los tres vectores determinada por las medianas
de un triángulo dirigido desde los vértices es cero.
Pregunta 3. ABCD es un paralelogramo y P es el punto de intersección de sus diagonales. Si O es el origen de la referencia, demuestre que 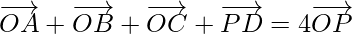

Solución:
Dado que ABCD es un paralelogramo, P es el punto de intersección de las diagonales y O el punto de referencia.
Entonces, usando la ley del triángulo en △AOP, obtenemos
-(1)
Usando la ley del triángulo en △OBP, obtenemos
-(2)
Usando la ley del triángulo en △OPC, obtenemos
-(3)
Usando la ley del triángulo en △OPD, obtenemos
-(4)
Ahora, al sumar las ecuaciones (1), (2), (3) y (4), obtenemos
Pregunta 4. Muestre que los segmentos de línea que unen los puntos medios de los lados opuestos de un cuadrilátero se bisecan entre sí.
Solución:

Consideremos ABCD como un cuadrilátero y P, Q, R, S como los puntos medios de los lados AB, BC, CD y DA.
Entonces, el vector de posición de A, B, C y D sea
Usando la fórmula del punto medio
Vector de posición de P =
Vector de posición de Q =
Vector de posición de R =
Vector de posición de S =
Vector de posición de
= Vector de posición de Q – Vector de posición de P
-(1)
Vector de posición de
= Vector de posición de R – Vector de posición de S
-(2)
De la ecuación (1) y (2),
Entonces, PQRS es un paralelogramo y PR biseca a QS -(como diagonales del paralelogramo)
Por lo tanto, demostró que los segmentos de recta que unen los puntos medios de
los lados opuestos de un cuadrilátero se bisecan entre sí.
Pregunta 5. ABCD son cuatro puntos en un plano y Q es el punto de intersección de las rectas que unen los puntos medios de AB y CD; a.C. y d.C. Muestre que 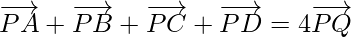 donde P es cualquier punto.
donde P es cualquier punto.
Solución:

Consideremos el vector de posición de los puntos A, B, C y D son
Usando la fórmula del punto medio, obtenemos
Vector de posición de AB =
Vector de posición de BC =
Vector de posición de CD =
Vector de posición de DA =
Se da que Q es el punto medio de la recta que une los puntos medios de AB y CD, por lo que
Ahora, supongamos que
es el vector de posición de P.
Asi que,
Por lo tanto probado
Pregunta 6. Demostrar por el método vectorial que las bisectrices internas de los ángulos de un triángulo son concurrentes.
Solución:

En el triángulo ABC, supongamos que los vectores de posición de los vértices del triángulo son
Longitud de los lados:
BC = x
CA = y
AB = z
En el triángulo ABC, la bisectriz interna divide el lado opuesto en la proporción de los lados que contienen los ángulos.
Como AD es la bisectriz interna del ∠ABC, entonces
BD/DC = AB/AC = z/y -(1)
Por lo tanto, el vector de posición de D =
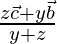
Deje que la bisectriz interna se corte en el punto I.
DI/IA = BD/AB -(2)
BD/DC = z/y
Por lo tanto,
CD/BD = z/y
(CD + BD)/BD = (y + z)/z
BC/BD = (y + z)/z
BD = ln/y + z -(3)
Entonces, de la ecuación (2) y (3), obtenemos
DI/IA = ln/(y +z)
Por lo tanto,
Vector de posición de I =
De manera similar, también podemos probar que me encuentro en las bisectrices internas de ∠B y ∠C.
Por lo tanto, las bisectrices son concurrentes.