Pregunta 1. Si el vector de posición de un punto (-4,-3) es 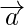 , encuentra
, encuentra 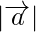 .
.
Solución:
Tenemos,
Pregunta 2. Si el vector 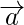 de posición de un punto (12,n) es tal que
de posición de un punto (12,n) es tal que 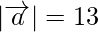 , encuentra los valores.
, encuentra los valores.
Solución:
Tenemos,
Al cuadrar ambos lados,
Pregunta 3. Encuentra un vector de 4 unidades de magnitud que sea paralelo al vector ![Rendered by QuickLaTeX.com \sqrt[]{3} \hat i + \hat{j}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a97850b84826eb14a2e57cb1eb52e9cd_l3.png) .
.
Solución:
Dado,
Sea
un vector paralelo a
Por lo tanto,para cualquier escalar
Pregunta 4. Expresar 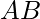 en términos de vectores unitarios (i)A = (4,-1),B = (1,3) (ii)A = (-6,3) , B = (-2,-5)
en términos de vectores unitarios (i)A = (4,-1),B = (1,3) (ii)A = (-6,3) , B = (-2,-5)
Solución:
(i) Tenemos,
A = (4,-1)
B = (1,3)
Vector de posición de A =
Vector de posición de B =
Ahora,
por lo tanto,(ii) Tenemos,
A = (-6,3)
B = (-2,-5)
Vector de posición de A =
Vector de posición de B =
Ahora,
por lo tanto,
Pregunta 5. Encuentra las coordenadas de la punta del vector de posición que es equivalente a 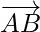 , donde las coordenadas de A y B son (-1,3) y (-2,1)
, donde las coordenadas de A y B son (-1,3) y (-2,1)
Solución:
Tenemos,
A = (-1,3)
B = (-2,1)
Ahora,
Vector de posición de
Vector de posición de
Por lo tanto,
Coordenada del vector de posición
Pregunta 6. ABCD es un paralelogramo. Si las coordenadas de A,B,C son (-2,-1), (3,0),(1,-2) respectivamente, encuentre las coordenadas de D.
Solución:
Aquí, A = (-2,-1)
B = (3,0)
C = (1,-2)
Supongamos que D sea (x, y).
Calculando el vector de posición de AB, tenemos,
= Vector de posición de B – Vector de posición de A
Comparando LHS y RHS de ambos,
5 = 1-x
X = -4
Y,
1 = -2-y
y = -3
Entonces, coordenadas de D = (-4,-3).
Pregunta 7. Si los vectores de posición de los puntos A(3,4), B(5,-6) y C(4,-1) son 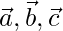 respectivamente, calcula el valor de
respectivamente, calcula el valor de 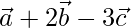 .
.
Solución:
Calculando los vectores de posición de todos los puntos que tenemos,
Ahora,
Cálculo del valor final después de sustituir los valores,
Cuestión 8. Si 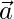 es el vector de posición cuya punta es (-5,3), hallar las coordenadas de un punto B tal que
es el vector de posición cuya punta es (-5,3), hallar las coordenadas de un punto B tal que 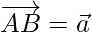 , siendo las coordenadas de A (-4,1).
, siendo las coordenadas de A (-4,1).
Solución:
Dado,
Coordenada de A = (4,-1)
Vector de posición de A =
Vector de posición de
Sea coordenada del punto B = (x, y)
Vector de posición de B =
Dado que,
Vector de posición de B – Vector de posición de A = \ vec{a}
Comparando los coeficientes de LHS y RHS
x – y = 5
x = 9
Además,
y + 1 = 3
y = -1
Entonces, coordenada de B = (9,-4)
Pregunta 9. Demuestra que los puntos 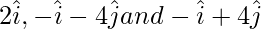 forman un triángulo isósceles.
forman un triángulo isósceles.
Solución:
Entonces, los dos lados AB y AC del triángulo ABC son iguales.
Por lo tanto, ABC es un triángulo isósceles.
Pregunta 10. Encuentra un vector unitario paralelo al vector  .
.
Solución:
Tenemos,
Dejar
Supongamos
que cualquier vector es paralelo a
, donde λ es cualquier escalar.
vector unitario de
Por lo tanto,
Pregunta 11. Encuentra las componentes a lo largo de los ejes de coordenadas del vector de posición de cada uno de los siguientes puntos:
(yo) P(3,2)
(ii) Q(-5,1)
(iii) R(-11,-9)
(iv) S(4,-3)
Solución:
(i) Dado, P = (3,2)
Vector de posición de P =
Componente de P a lo largo del eje x =
Componente de P a lo largo del eje y =
(ii) Dado, Q = (-5,1)
Vector de posición de Q =
Componente de Q a lo largo del eje x =
Componente de Q a lo largo del eje y =
(iii) Dado, R = (-11,-9)
Vector de posición de R =
Componente de R a lo largo del eje x =
Componente de R a lo largo del eje y =
(iv) Dado, S = (4,-3)
Vector de posición de S =
Componente de S a lo largo del eje x =
Componente de S a lo largo del eje y =
![Rendered by QuickLaTeX.com \overrightarrow{a} = -4\hat i - 3\hat j \\|\overrightarrow{a}| = \sqrt[]{(-4)^2+ (-3)^2} \\ = \sqrt[]{16+9} \\ = \sqrt[]{25} \\= 5 \\|\overrightarrow{a}| = 5](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-77aba2bfd31d2156b1b8f1b26dda4a40_l3.png)
![Rendered by QuickLaTeX.com \overrightarrow{a} = 12\hat i + n \hat j \\ |\overrightarrow{a}| = \sqrt[]{12^2 + n^2} \\ 13 = \sqrt[]{144 + n^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9f61693cf554f5e955cac011d991fb45_l3.png)
![Rendered by QuickLaTeX.com (13)^2 = (\sqrt[]{144 + n^2})^2 \\169 = 144 + n^2 \\n^2 = 169 - 144 \\n^2 = 25 \\n^2 = \pm \sqrt[]{25} \\n = \pm 5](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c89701bda81788c9e282fe8ac731c7b3_l3.png)
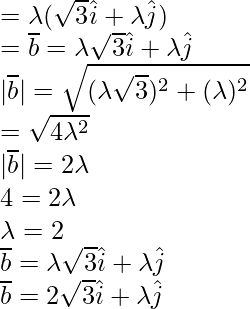
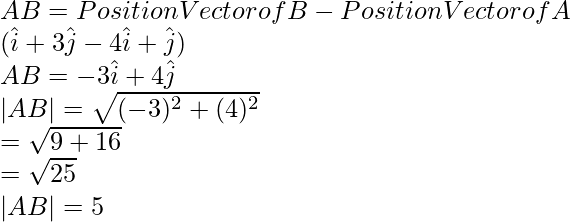
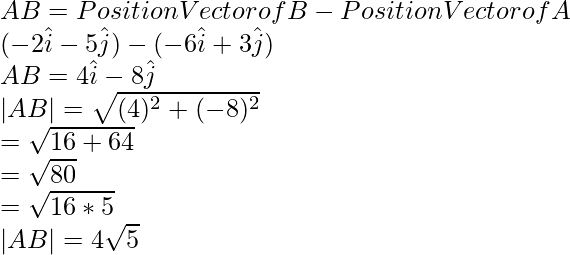
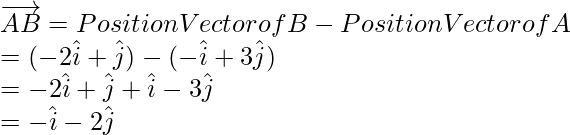
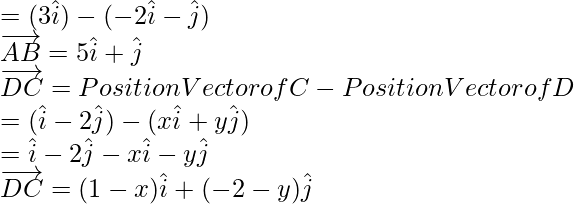
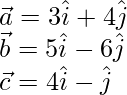

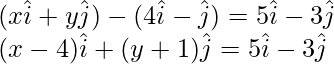
![Rendered by QuickLaTeX.com |\overrightarrow{AB}| = 5 units \\ |\overrightarrow{BC}| = \sqrt[]{8^2} \\ |\overrightarrow{BC}| = 8 units \\ |\overrightarrow{AC}| = \sqrt[]{(-3)^2 + (8)^2} \\ = \sqrt[]{9+16} \\ = \sqrt[]{25} \\Here, \\|\overrightarrow{AB}| = |\overrightarrow{AC}|](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c9e9c94ef1a72498797e90693c8f5a11_l3.png)
![Rendered by QuickLaTeX.com \vec{b}= \frac{\vec{b}}{|\vec{b}|} \\ \hat{b} = \frac{\hat i + \sqrt[]{3} \hat j}{2} \\ \hat{b} = \frac{1}{2}(\hat i + \sqrt[]{3} \hat j)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e3fb617eacbca6e8d31a760e6770a92a_l3.png)