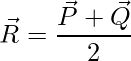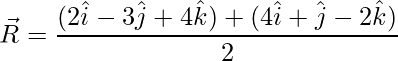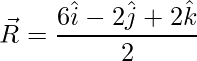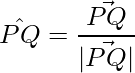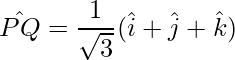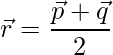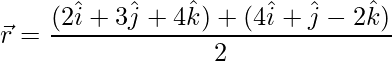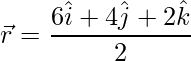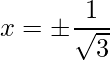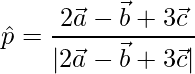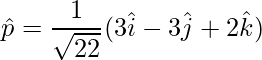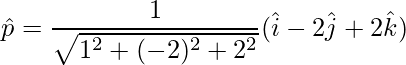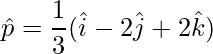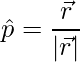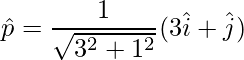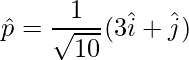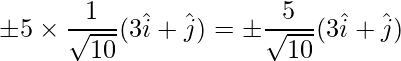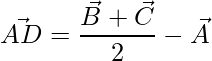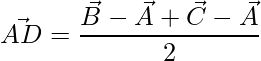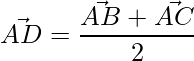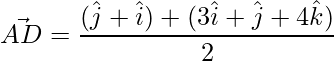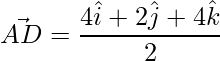Pregunta 11: Encuentra el vector de posición del punto medio del vector que une los puntos P( 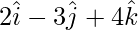 ) y Q(
) y Q(  ).
).
Solución:
El punto medio del segmento de recta que une 2 vectores viene dado por:
=>
=>
=>
=>
Pregunta 12: Encuentra el vector unitario en la dirección del vector 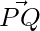 , donde P y Q son los puntos (1,2,3) y (4,5,6).
, donde P y Q son los puntos (1,2,3) y (4,5,6).
Solución:
Dejar,
=>
=>
=>
=>
=>
vector unitario es,
=>
=>
=>
=>
Pregunta 13: Demuestra que los puntos A( 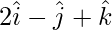 ), B(
), B( 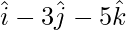 ), C(
), C(  ) son los vértices de un triángulo rectángulo.
) son los vértices de un triángulo rectángulo.
Solución:
Dejar,
=>
=>
=>
Los segmentos de línea son,
=>
=>
=>
=>
=>
=>
=>
=>
=>
Las magnitudes de los lados son,
=>
=>
=>
Como podemos ver que
=> Por lo tanto, ABC es un triángulo rectángulo.
Pregunta 14: Encuentra el vector de posición del punto medio del vector que une los puntos P(2, 3, 4) y Q(4, 1, -2).
Solución:
Dejar,
=>
=>
El punto medio del segmento de recta que une 2 vectores viene dado por:
=>
=>
=>
=>
Pregunta 15: Encuentra el valor de x para el cual x( 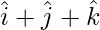 ) es un vector unitario.
) es un vector unitario.
Solución:
La magnitud del vector dado es,
=>
=>
=>
Para que sea un vector unitario,
=>
=>
=>
Pregunta 16: Si 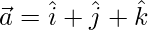 ,
, 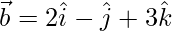 y
y 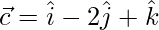 , encuentran un vector unitario paralelo a
, encuentran un vector unitario paralelo a 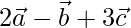 .
.
Solución:
Dado
,
y
=>
=>
Por lo tanto, el vector unitario es,
=>
=>
=>
Pregunta 17: Si 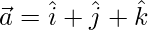 ,
, 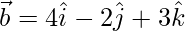 y
y 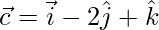 , encuentre un vector de 6 unidades de magnitud que sea paralelo al vector
, encuentre un vector de 6 unidades de magnitud que sea paralelo al vector 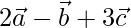 .
.
Solución:
Dado
,
y
=>
=>
El vector unitario en esa dirección es,
=>
=>
=>
Dado que el vector tiene una magnitud de 6,
=> Los vectores requeridos son:
=
Pregunta 18: Encuentra un vector de magnitud 5 unidades paralelo a la resultante del vector 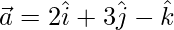 y
y 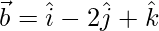 .
.
Solución:
dado,
y
El vector resultante estará dado por,
=>
=>
=>
vector unitario es,
=>
=>
=>
Dado que el vector tiene una magnitud de 5,
=> Los vectores requeridos son:
Pregunta 19: Los dos vectores 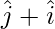 y
y 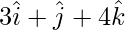 representan los lados
representan los lados 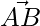 y
y 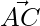 respectivamente del triángulo ABC. Encuentre la longitud de la mediana a través de A.
respectivamente del triángulo ABC. Encuentre la longitud de la mediana a través de A.
Solución:
Sea D el punto de BC en el que toca la mediana que pasa por A.
D es también el punto medio de BC.
Así, la mediana
viene dada por:
=>
=>
=>
=>
=>
=>
Por lo tanto, la longitud de la mediana es,
=>
=>
=>
unidades