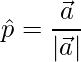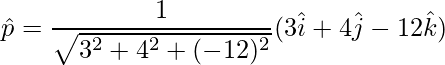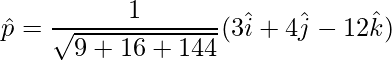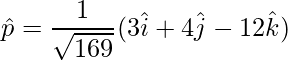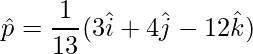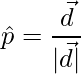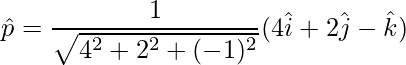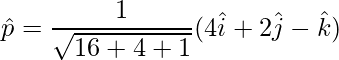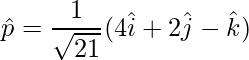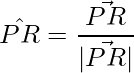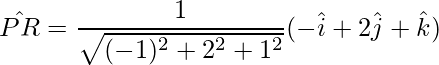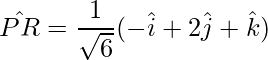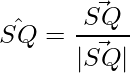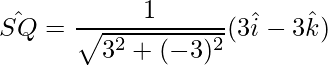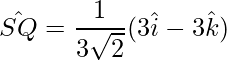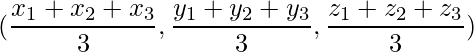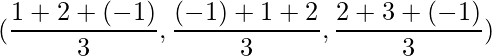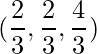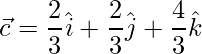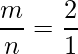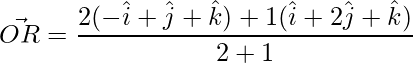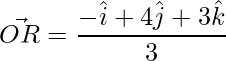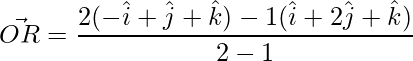Clase 12 Soluciones RD Sharma – Capítulo 23 Álgebra de Vectores – Ejercicio 23.6 | Serie 1

Posted on by Rudeus Greyrat

Pregunta 1: Encuentra la magnitud del vector 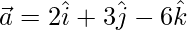 \vec{a} = 2\hat{i}+3\hat{j}-6\hat{k} .

Solución:

Magnitud de un vector x\hat{i}+y\hat{j}+z\hat{k} = \sqrt{x^2+y^2+z^2}

=> |\vec{a}| = \sqrt{2^2+3^2+(-6)^2}

=> |\vec{a}| = \sqrt{4+9+36}

=> |\vec{a}| = \sqrt{49}

=> |\vec{a}| = 7

Pregunta 2: Encuentra el vector unitario en la dirección de 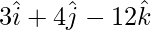 3\hat{i}+4\hat{j}-12\hat{k} .

Solución:

Sabemos que el vector unitario de un vector  \vec{a}  viene dado por,

=> \hat{p} = \dfrac{\vec{a}}{|\vec{a}|}

=> \hat{p} = \dfrac{1}{\sqrt{3^2+4^2+(-12)^2}}(3\hat{i}+4\hat{j}-12\hat{k})

=> \hat{p} = \dfrac{1}{\sqrt{9+16+144}}(3\hat{i}+4\hat{j}-12\hat{k})

=> \hat{p} = \dfrac{1}{\sqrt{169}}(3\hat{i}+4\hat{j}-12\hat{k})

=> \hat{p} = \dfrac{1}{13}(3\hat{i}+4\hat{j}-12\hat{k})

Pregunta 3: Encuentra un vector unitario en la dirección de la resultante de los vectores 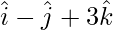 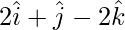\hat{i}-\hat{j}+3\hat{k},  2\hat{i}+\hat{j}-2\hat{k}  y  \hat{i}+2\hat{j}-2\hat{k}.

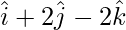Solución:

Dejar,

=> \vec{a} = \hat{i}-\hat{j}+3\hat{k}

=> \vec{b} = 2\hat{i}+\hat{j}-2\hat{k}

=> \vec{c} = \hat{i}+2\hat{j}-2\hat{k}

Sea  \vec{d}  la resultante,

=> \vec{d} = \vec{a} + \vec{b} + \vec{c}

=> \vec{d} = (\hat{i}-\hat{j}+3\hat{k})+(2\hat{i}+\hat{j}-2\hat{k})+(\hat{i}+2\hat{j}-2\hat{k})

=> \vec{d} = 4\hat{i}+2\hat{j}-\hat{k}

vector unitario es,

=> \hat{p} = \dfrac{\vec{d}}{|\vec{d}|}

=> \hat{p} = \dfrac{1}{\sqrt{4^2+2^2+(-1)^2}}(4\hat{i}+2\hat{j}-\hat{k})

=> \hat{p} = \dfrac{1}{\sqrt{16+4+1}}(4\hat{i}+2\hat{j}-\hat{k})

=> \hat{p} = \dfrac{1}{\sqrt{21}}(4\hat{i}+2\hat{j}-\hat{k})

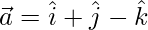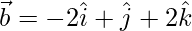Pregunta 4: Los lados adyacentes de un paralelogramo están representados por los vectores  \vec{a}=\hat{i}+\hat{j}-\hat{k}  y  \vec{b}=-2\hat{i}+\hat{j}+2\hat{k}. Encuentra los vectores unitarios paralelos a las diagonales del paralelogramo.

Solución:

Sea PQRS el paralelogramo.

Dado que, PQ =  \hat{i}+\hat{j}-\hat{k} y QR =  -2\hat{i}+\hat{j}+2\hat{k}.

Así, las diagonales son: PR y SQ.

=> \vec{PR} = \vec{PQ} + \vec{QR}

=> \vec{PR} = \vec{a} + \vec{b}

=> \vec{PR} = (\hat{i}+\hat{j}-\hat{k})+(-2\hat{i}+\hat{j}+2\hat{k})

=> \vec{PR} = -\hat{i} + 2\hat{j} +\hat{k}

=> \vec{SQ} = \vec{PQ} - \vec{PS}

=> \vec{SQ} = \vec{a} - \vec{b}

=> \vec{SQ} = (\hat{i}+\hat{j}-\hat{k})-(-2\hat{i}+\hat{j}+2\hat{k})

=> \vec{SQ} = 3\hat{i}-3\hat{k}

Así, los vectores unitarios en la dirección de las diagonales son:

=> \hat{PR} = \dfrac{\vec{PR}}{|\vec{PR}|}

=> \hat{PR} = \dfrac{1}{\sqrt{(-1)^2+2^2+1^2}}( -\hat{i} + 2\hat{j} +\hat{k})

=> \hat{PR} = \dfrac{1}{\sqrt{6}}(-\hat{i}+2\hat{j}+\hat{k})

=> \hat{SQ} = \dfrac{\vec{SQ}}{|\vec{SQ}|}

=> \hat{SQ} = \dfrac{1}{\sqrt{3^2+(-3)^2}}( 3\hat{i}-3\hat{k})

=> \hat{SQ} = \dfrac{1}{3\sqrt{2}}(3\hat{i}-3\hat{k})

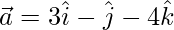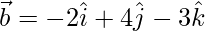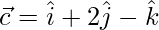Pregunta 5: Si \vec{a} = 3\hat{i}-\hat{j}-4\hat{k},  \vec{b}= -2\hat{i}+4\hat{j}-3\hat{k}  y  \vec{c}=\hat{i}+2\hat{j}-\hat{k}, encuentran  |3\vec{a}-2\vec{b}+4\vec{c}|.

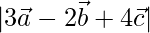Solución:

Dado,  \vec{a} = 3\hat{i}-\hat{j}-4\hat{k},  \vec{b}= -2\hat{i}+4\hat{j}-3\hat{k} y  \vec{c}=\hat{i}+2\hat{j}-\hat{k}.

Dejar,

=> \vec{d} = 3\vec{a}-2\vec{b}+4\vec{c}

=> \vec{d} = 3(3\hat{i}-\hat{j}-4\hat{k})-2(-2\hat{i}+4\hat{j}-3\hat{k})+4(\hat{i}+2\hat{j}-\hat{k})

=> \vec{d} = (9\hat{i}-3\hat{j}-12\hat{k})+ (4\hat{i}-8\hat{j}+6\hat{k})+(4\hat{i}+8\hat{j}-4\hat{k})

=> \vec{d} = 17\hat{i}-3\hat{j}-10\hat{k}

La magnitud está dada por,

=> |\vec{d}| = \sqrt{17^2+(-3)^2+(-10)^2}

=> |\vec{d}| = \sqrt{289+9+100}

=> |\vec{d}| = \sqrt{398}

Pregunta 6: Si 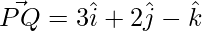 \vec{PQ} = 3\hat{i}+2\hat{j}-\hat{k}  y las coordenadas de P son (1,-1,2), encuentre las coordenadas de Q.

Solución:

Dado, \vec{PQ} = 3\hat{i}+2\hat{j}-\hat{k}

Y, \vec{P} = \hat{i}-\hat{j}+2\hat{k}

=> \vec{PQ} = \vec{Q}-\vec{P}

=> \vec{Q} = \vec{PQ}+ \vec{P}

=> \vec{Q} = (3\hat{i}+2\hat{j}-\hat{k})+(\hat{i}-\hat{j}+2\hat{k})

=> \vec{Q} = 4\hat{i}+\hat{j}+\hat{k}

=> Así las coordenadas de Q son (4,1,1).

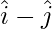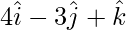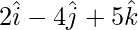Pregunta 7: Demuestra que los puntos  \hat{i}-\hat{j},  4\hat{i}-3\hat{j}+\hat{k} y  2\hat{i}-4\hat{j}+5\hat{k} son los vértices de un triángulo rectángulo.

Solución:

Dejar,

=> \vec{A} = \hat{i}-\hat{j}

=> \vec{B} = 4\hat{i}-3\hat{j}+\hat{k}

=> \vec{C} = 2\hat{i}-4\hat{j}+5\hat{k}

Por lo tanto, los 3 lados del triángulo son,

=> \vec{AB} = \vec{B} - \vec{A}

=> \vec{AB} = (4\hat{i}-3\hat{j}+\hat{k})-(\hat{i}-\hat{j})

=> \vec{AB} = 3\hat{i}-2\hat{j}+\hat{k}

=> \vec{BC} = \vec{C} - \vec{B}

=> \vec{BC} = (2\hat{i}-4\hat{j}+5\hat{k})-(4\hat{i}-3\hat{j}+\hat{k})

=> \vec{BC} = -2\hat{i}-\hat{j}+4\hat{k}

=> \vec{CA} = \vec{A} -\vec{C}

=> \vec{CA} = ( \hat{i}-\hat{j})-(2\hat{i}-4\hat{j}+5\hat{k})

=> \vec{CA} = -\hat{i}+3\hat{j}-5\hat{k}

Las longitudes de cada lado están dadas por su magnitud,

=> |\vec{AB}| = \sqrt{3^2+(-2)^2+1^2} = \sqrt{14}

=> |\vec{BC}| = \sqrt{(-2)^2+(-1)^2+4^2} = \sqrt{21}

=> |\vec{CA}| = \sqrt{(-1)^2+3^2+(-5)^2} = \sqrt{35}

Como podemos ver,

=> |\vec{CA}|^2 = |\vec{AB}|^2+|\vec{BC}|^2

=> Estos 3 puntos forman un triángulo rectángulo.

Pregunta 8: Si los vértices A, B y C de un triángulo ABC son los puntos con vectores posición 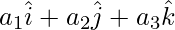 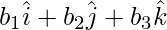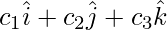a_1\hat{i}+a_2\hat{j}+a_3\hat{k} ,  b_1\hat{i}+b_2\hat{j}+b_3\hat{k} ,  c_1\hat{i}+c_2\hat{j}+c_3\hat{k}  respectivamente, ¿cuáles son los vectores determinados por sus lados? Encuentre la longitud de estos vectores.

Solución:

Dejar,

=> \vec{a} =a_1\hat{i}+a_2\hat{j}+a_3\hat{k}

=> \vec{b} = b_1\hat{i}+b_2\hat{j}+b_3\hat{k}

=> \vec{c} = c_1\hat{i}+c_2\hat{j}+c_3\hat{k}

Los lados del triángulo se dan como,

=> \vec{AB} = \vec{b} - \vec{a}

=> \vec{AB} = ( b_1\hat{i}+b_2\hat{j}+b_3\hat{k})-(a_1\hat{i}+a_2\hat{j}+a_3\hat{k})

=> \vec{AB} = (b_1-a_1)\hat{i}+(b_2-a_2)\hat{j}+(b_3-a_3)\hat{k}

=> \vec{BC} = \vec{c}-\vec{b}

=> \vec{BC} = ( c_1\hat{i}+c_2\hat{j}+c_3\hat{k})-(b_1\hat{i}+b_2\hat{j}+b_3\hat{k})

=> \vec{BC} = (c_1-b_1)\hat{i}+(c_2-b_2)\hat{j}+(c_3-b_3)\hat{k}

=> \vec{CA} = \vec{a}-\vec{c}

=> \vec{CA} = ( a_1\hat{i}+a_2\hat{j}+a_3\hat{k})-(c_1\hat{i}+c_2\hat{j}+c_3\hat{k})

=> \vec{CA} = (a_1-c_1)\hat{i}+(a_2-c_2)\hat{j}+(a_3-c_3)\hat{k}

Las longitudes de los lados son,

=> |\vec{AB}| = \sqrt{(b_1-a_1)^2+(b_2-a_2)^2+(b_3-a_3)^2}

=> |\vec{BC}| = \sqrt{(c_1-b_1)^2+(c_2-b_2)^2+(c_3-b_3)^2}

=> |\vec{CA}| = \sqrt{(a_1-c_1)^2+(a_2-c_2)^2+(a_3-c_3)^2}

Pregunta 9: Encuentra el vector desde el origen O hasta el baricentro del triángulo cuyos vértices son (1,-1,2), (2,1,3) y (-1,2,-1).

Solución:

La posición del baricentro está dada por,

=> (x, y, z) = (\dfrac{x_1+x_2+x_3}{3},\dfrac{y_1+y_2+y_3}{3},\dfrac{z_1+z_2+z_3}{3})

=> (x, y, z) = (\dfrac{1+2+(-1)}{3},\dfrac{(-1)+1+2}{3},\dfrac{2+3+(-1)}{3})

=> (x, y, z) = (\dfrac{2}{3},\dfrac{2}{3},\dfrac{4}{3})

El vector al baricentro de O es,

=> \vec{c} = \dfrac{2}{3}\hat{i}+\dfrac{2}{3}\hat{j}+\dfrac{4}{3}\hat{k}

Pregunta 10: Encuentra el vector de posición de un punto R que divide el segmento de recta que une los puntos p( 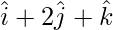\hat{i}+2\hat{j}+\hat{k} ) y q( 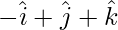-\hat{i}+\hat{j}+\hat{k}) en la razón 2:1.

(i) Internamente

Solución:

Los vectores de posición de un punto que divide internamente un segmento de línea están dados por,

=>  \vec{OR} = \dfrac{m\vec{Q}+n\vec{P}}{m+n} , donde \dfrac{m}{n}=\dfrac{2}{1}

=> \vec{OR} = \dfrac{2(-\hat{i}+\hat{j}+\hat{k})+1(\hat{i}+2\hat{j}+\hat{k})}{2+1}

=> \vec{OR} = \dfrac{-\hat{i}+4\hat{j}+3\hat{k}}{3}

(ii) Externamente

Solución:

Los vectores de posición de un punto que divide externamente un segmento de línea están dados por,

=>  \vec{OR} = \dfrac{m\vec{Q}-n\vec{P}}{m-n} , donde \dfrac{m}{n}=\dfrac{2}{1}

=> \vec{OR} = \dfrac{2(-\hat{i}+\hat{j}+\hat{k})-1(\hat{i}+2\hat{j}+\hat{k})}{2-1}

=> \vec{OR} = 3\hat{i}-\hat{k}

Publicación traducida automáticamente

Artículo escrito por isha412k y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *