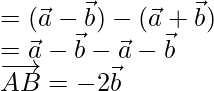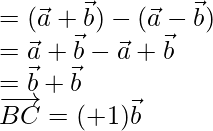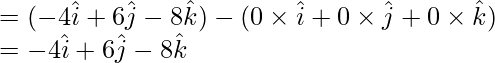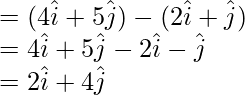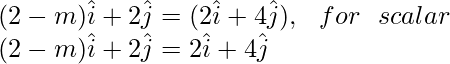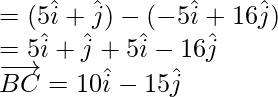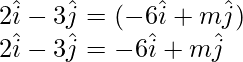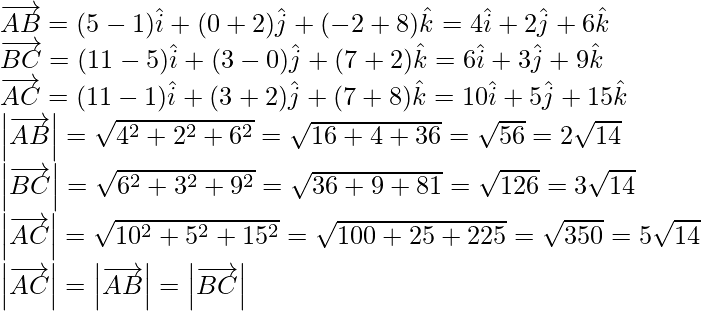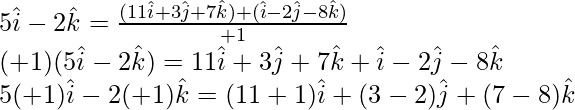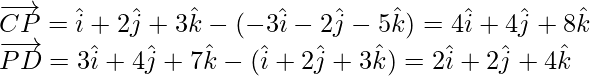Pregunta 1. Demuestre que los puntos A, B, C con vectores de posición 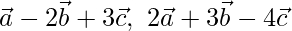 y
y 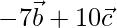 son colineales.
son colineales.
Solución:
Dado que,
Vector de posición de
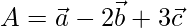
Vector de posición de
Vector de posición de
= Vector de posición B – Vector de posición de A
=
= Vector de posición de C – Vector de posición de B
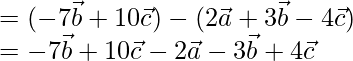
=
Usando
y
, obtenemos,
Entonces,
||
pero
es un vector común.
Por lo tanto, se demostró que A, B, C son colineales.
Pregunta 2 (i). Si 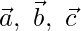 son vectores no coplanares, demuestre que los puntos que tienen los vectores de posición
son vectores no coplanares, demuestre que los puntos que tienen los vectores de posición 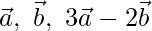 son colineales.
son colineales.
Solución:
Supongamos tres puntos que son A, B, C
Vector de posición de A =
Vector de posición de B =
Vector de posición de C =
= Vector de posición de B – Vector de posición de A
=
-(1)
= Vector de posición de C – Vector de posición de B
-(2)
Usando la ecuación (1) y (2), obtenemos
=
Al comparar los coeficientes de LHS y RHS,
-λ = 3
λ = 3
λ = -3
El valor de λ es diferente
Por lo tanto, los puntos A, B, C no son colineales.
Pregunta 2 (ii) Si 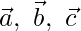 son vectores no coplanares, demuestre que los puntos que tienen los vectores de posición
son vectores no coplanares, demuestre que los puntos que tienen los vectores de posición 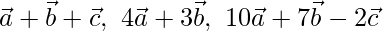 son colineales.
son colineales.
Solución:
Supongamos tres puntos que son A, B, C
Vector de posición de A =
Vector de posición de B =
Vector de posición de C =
= Vector de posición de B – Vector de posición de A
=
= Vector de posición de C – Vector de posición de B
Usando
y
obtenemos
= 2
Entonces,
||
pero
es un vector común.
Por lo tanto, A, B, C son colineales
Pregunta 3. Demuestra que los puntos que tienen vectores de posición 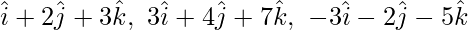 son colineales.
son colineales.
Solución:
Consideremos los puntos A, B, C
Vector de posición de A =
Vector de posición de B =
Vector de posición de C =
= Vector de posición de B – Vector de posición de A
=
= Vector de posición de C – Vector de posición de B
Usando
y
obtenemos
= -3
||
pero
es un vector común.
Por lo tanto, A, B, C son colineales
Pregunta 4. Si los puntos con vectores de posición 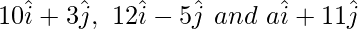 son colineales, encuentra el valor de a.
son colineales, encuentra el valor de a.
Solución:
Sean los puntos A, B, C
Vector de posición de A =
Vector de posición de B =
Vector de posición de C =
Dado que A, B, C son colineales
⇒
y
son colineales
⇒
=
⇒ Vector de posición de B – Vector de posición de A = B)
Al comparar los coeficientes de LHS y RHS, obtenemos
Ahora pon el valor de
Entonces, el valor de a es 8.
Pregunta 5. Si  son dos vectores no colineales, demuestre que los puntos con vectores de posición
son dos vectores no colineales, demuestre que los puntos con vectores de posición  son colineales para todos los valores reales de
son colineales para todos los valores reales de
Solución:
Consideremos los puntos A, B, C
Vector de posición de A =
Vector de posición de B =
Vector de posición de C =
= Vector de posición de B – Vector de posición de A
= Vector de posición de C – Vector de posición de B
usando
y
=
Sea
= μ
Como μ también es un número real.
||
pero
es un vector común.
Por lo tanto, A, B, C son colineales.
Pregunta 6. Si 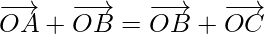 , prueba que A, B, C son puntos colineales
, prueba que A, B, C son puntos colineales
Solución:
Según la pregunta
Entonces,
||
pero
es un vector común.
Por lo tanto, A, B, C son colineales.
Pregunta 7. Demuestre que los vectores 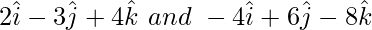 son colineales.
son colineales.
Solución:
Consideremos, el vector de posición A =
Vector de posición B =
Supongamos que O es el punto inicial que tiene el vector de posición
= Vector de posición de A – Vector de posición de O
= Vector de posición de B – Vector de posición de O
Usando OA y OB, obtenemos
Por lo tanto,
||
pero O es el punto común para ellos.
Por lo tanto, A y B son colineales.
Pregunta 8. Si los puntos A(m, -1), B(2, 1), C(4, 5) son colineales, encuentra el valor de m.
Solución:
Consideremos
A = (m, -1)
B = (2, 1)
C = (4, 5)
= Vector de posición de B – Vector de posición de A
= Vector de posición de C – Vector de posición de B
A, B, C son colineales.
Entonces,
y
son colineales.
Entonces,
=
Al comparar el coeficiente de LHS y RHS, obtenemos
2-m = 2
-(1)
2 = 4
=
= -(2)
De la ecuación (1) y (2), obtenemos
4 – 2m = 2
-2m = 2 – 4
metro =
metro = 1
entonces el valor de m es 1
Pregunta 9. Demuestra que los puntos (3, 4), (-5, 16), (5, 1) son colineales.
Solución:
Deja que su considerado
A = (3, 4)
B = (-5, 16)
C = (5, 1)
= Vector de posición de B – Vector de posición de A
= Vector de posición de C – Vector de posición de B
Asi que,
||
pero B es un punto común.
Por lo tanto, A, B, C son colineales.
Pregunta 10. Si los vectores 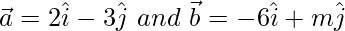 son colineales, encuentra el valor de m.
son colineales, encuentra el valor de m.
Solución:
Dado:
y
son colineales.
Entonces, un =
Al comparar los coeficientes de LHS y RHS, obtenemos
2 = -6λ
λ = 2/(-6)
λ = -1/3 -(1)
-3 = λm
λ = -3/m -(2)
De la ecuación (1) y (2), tenemos
-1/3 = -3/m
m = 3 × 3
metro = 9
entonces el valor de m es 9
Pregunta 11. Demuestra que los puntos A(1, -2, -8), B(5, 0, -2) y C(11, 3, 7) son colineales y encuentra la razón en que B divide a AC.
Solución:
Dado: A(1, -2, -8), B(5, 0, -2) y C(11, 3, 7).
Entonces los puntos dados son colineales
Ahora, consideremos el punto B dividiendo AC en la razón
5(
⇒ 6
Entonces, el punto B divide a AC en la razón 2 : 3.
Pregunta 12. Usando el vector, demuestre que los puntos A(-2, 3, 5), B(7, 0, -1) y C(-3, -2, -5) y D(3, 4, 7) son tal que AB y CD se cortan en el punto P(1, 2, 3).
Solución:
De acuerdo con la pregunta, tenemos,
= Vector de posición de P – Vector de posición de A
= Vector de posición de B – Vector de posición de P
Por lo tanto,
. Entonces, los vectores son colineales.
Pero P es un punto común, por lo que P, A, B son puntos colineales.
Similarmente,
son colineales,
Pero P es un punto común a
. Entonces, C, P, D son puntos colineales.
Por lo tanto, AB y CD se cortan en el punto P.
Pregunta 13. Usando vectores, encuentre el valor de I tal que los puntos (I, -10, 3), (1, -1, 3) y (3, 5, 3) sean colineales.
Solución:
Dado: Puntos (I
x = 5/2 y y = -3/2
Ahora, pon el valor de x e y en la ecuación (1), obtenemos
yo = -2
Entonces el valor de I es -2
Publicación traducida automáticamente
Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

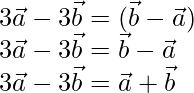
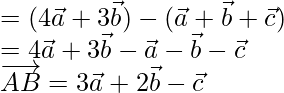
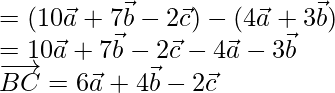
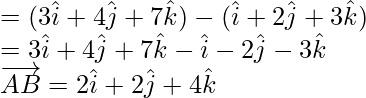
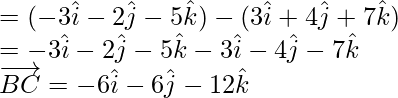
![Rendered by QuickLaTeX.com ⇒ (12\hat{i}-5\hat{j})-(10\hat{i}+3\hat{j})=λ[(a\hat{i}+11\hat{j})-(12\hat{i}-5\hat{j})]\\ ⇒ 12\hat{i}-5\hat{j}-10\hat{i}-3\hat{j}=λ(a\hat{i}+11\hat{j}-12\hat{i}+5\hat{j})]\\ ⇒ 2\hat{i}-8\hat{j}=(λa-12λ)\hat{i}=(11λ+5λ)\hat{j}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a8467d4a8d795a88587717ca5b67905f_l3.png)