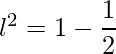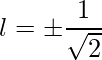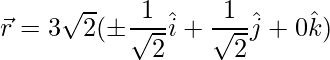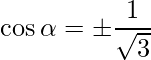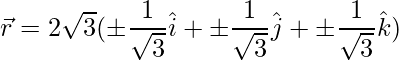Pregunta 1: ¿Puede un vector tener ángulos de dirección de 45°, 60° y 120°?
Solución:
Sabemos que si l, m y n son los cosenos directores y
,
y
son los ángulos directores entonces,
=>
=>
=>
También,
=> l 2 + metro 2 + norte 2 = 1
=>
=>
=> Como LHS = RHS, el vector puede tener estos ángulos de dirección.
Pregunta 2: Demuestra que 1,1 y 1 no pueden ser los cosenos directores de una recta.
Solución:
Dado que, l=1, m=1 y n=1.
Lo sabemos,
=> l 2 + metro 2 + norte 2 = 1
=> 1 2 + 1 2 + 1 2 = 1
=> 3 ≠ 1
Por lo tanto, 1, 1 y 1 nunca pueden ser los cosenos directores de una línea recta.
=> Por lo tanto probado.
Pregunta 3: Un vector forma un ángulo 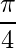 con cada uno de los ejes x e y. Encuentre el ángulo que forma con el eje z.
con cada uno de los ejes x e y. Encuentre el ángulo que forma con el eje z.
Solución:
Sabemos que si l, m y n son los cosenos directores y
,
y
son los ángulos directores entonces,
=>
=>
Sea
el ángulo que tenemos que calcular.
Lo sabemos,
=> l 2 + metro 2 + norte 2 = 1
=>
=> norte 2 = 1 – 1
=> norte 2 = 0
=>
=>
=>
=>
Pregunta 4: Un vector 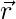 está inclinado en ángulos agudos iguales al eje x, eje y y eje z. Si
está inclinado en ángulos agudos iguales al eje x, eje y y eje z. Si 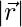 = 6 unidades, encuentre
= 6 unidades, encuentre 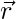 .
.
Solución:
Dado que
=>
=> l = metro = norte = pag (digamos)
Lo sabemos,
=> l 2 + metro 2 + norte 2 = 1
=> pag 2 + pag 2 + pag 2 = 1
=> 3p 2 = 1
=>
El vector
se puede describir como,
=>
=>
=>
Pregunta 5: Un vector 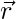 está inclinado al eje x a 45° y al eje y a 60°. Si
está inclinado al eje x a 45° y al eje y a 60°. Si 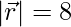 son unidades, encuentre
son unidades, encuentre 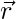 .
.
Solución:
Dado eso
y
Lo sabemos,
=> l 2 + metro 2 + norte 2 = 1
=>
=>
=>
=>
=>
=>
El vector
se puede describir como,
=>
=>
=>
Pregunta 6: Encuentra los cosenos directores de los siguientes vectores:
(i): 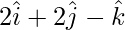
Solución:
Las relaciones de dirección se dan como 2, 2 y -1.
Los cosenos directores se dan como,
=>
=>
=>
(ii): 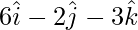
Solución:
Las relaciones de dirección se dan como 6, -2 y -3.
Los cosenos directores se dan como,
=>
=>
=>
(iii): 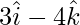
Solución:
Las relaciones de dirección se dan como 3, 0 y -4.
Los cosenos directores se dan como,
=>
=>
=>
Pregunta 7: Encuentra los ángulos en los que los siguientes vectores se inclinan a cada uno de los ejes de coordenadas.
(i): 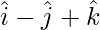
Solución:
Las relaciones de dirección dadas son: 1,-1,1.
De este modo,
=>
=>
=>
=>
=>
(ii): 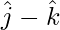
Solución:
Las relaciones de dirección dadas son: 0,1,-1.
De este modo,
=>
=>
=>
=>
=>
=>
(iii): 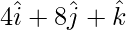
Solución:
Las relaciones de dirección dadas son: 4, 8, 1.
De este modo,
=>
=>
=>
=>
=>
Pregunta 8: Demuestra que el vector 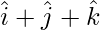 tiene la misma inclinación que los ejes OX, OY y OZ.
tiene la misma inclinación que los ejes OX, OY y OZ.
Solución:
Dejar
De este modo,
=>
Así, los cosenos directores son:
,
y
=>
De este modo,
=>
=> Así, el vector está igualmente inclinado con los 3 ejes.
Pregunta 9: Muestre que los cosenos directores de un vector igualmente inclinado a los ejes OX, OY y OZ son 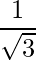 ,
, 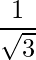 ,
, 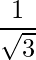 .
.
Solución:
Sea el vector igualmente inclinado en un ángulo de
.
Entonces los cosenos directores del vector l, m, n son:
,
y
Lo sabemos,
=> l 2 + metro 2 + norte 2 = 1
=>
=>
=>
=> Así, los cosenos directores son:
,
,
.
Pregunta 10: Si un vector unitario 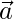 forma un ángulo
forma un ángulo  con
con 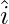 ,
, 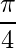 con
con 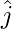 y un ángulo agudo
y un ángulo agudo 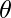 con
con 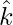 , entonces encuentre \theta y, por lo tanto, las componentes de
, entonces encuentre \theta y, por lo tanto, las componentes de 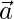 .
.
Solución:
El vector unitario ser,
=>
=>
Dado que
es un vector unitario,
=>
=>
=>
=>
=>
=>
=>
=>
=>
=>
Pregunta 11: Encuentre un vector 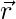 de unidades de magnitud
de unidades de magnitud 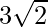 que forme un ángulo de
que forme un ángulo de 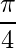 y
y 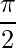 con los ejes y y z respectivamente.
con los ejes y y z respectivamente.
Solución:
Sean l, m, n los cosenos directores del vector
.
Lo sabemos,
=> l 2 + metro 2 + norte 2 = 1
=>
=>
=>
=>
Así el vector es,
=>
=>
=>
Pregunta 12: Un vector 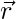 está inclinado en ángulos iguales a los 3 ejes. Si la magnitud de
está inclinado en ángulos iguales a los 3 ejes. Si la magnitud de 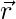 es
es 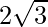 , encuentre
, encuentre 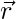 .
.
Solución:
Sean l, m, n los cosenos directores del vector
.
Dado que el vector está inclinado en ángulos iguales a los 3 ejes.
=>
Lo sabemos,
=> l 2 + metro 2 + norte 2 = 1
=>
=>
Por lo tanto, el vector se da como,
=>
=>
=>
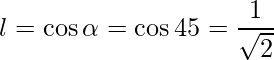
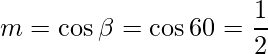
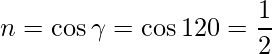
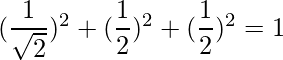
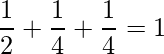
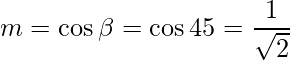
![Rendered by QuickLaTeX.com n^2 = 1- [(\dfrac{1}{\sqrt{2}})^2+(\dfrac{1}{\sqrt{2}})^2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-11b5e5562f22f79b315f5ec4d28cfad1_l3.png)
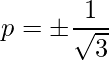
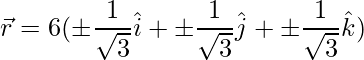
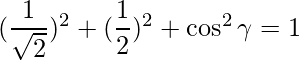
![Rendered by QuickLaTeX.com \cos^2 \gamma = 1- [\dfrac{1}{2}+\dfrac{1}{4}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-681e487ff624c315893ac985c72d6924_l3.png)
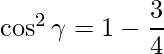
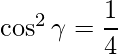
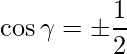
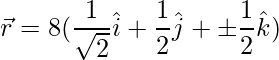
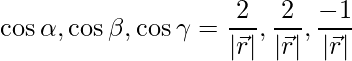
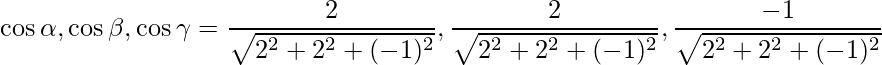
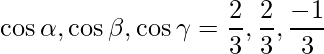
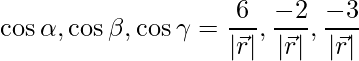
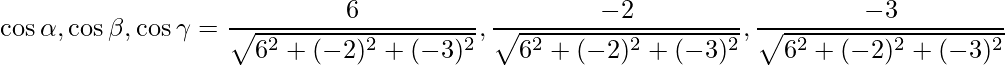
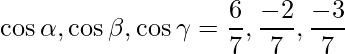
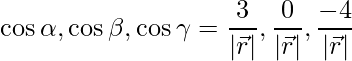
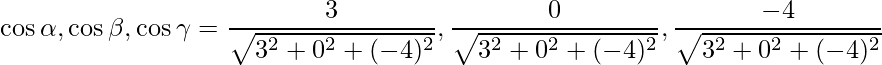
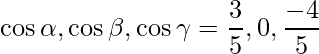
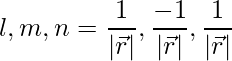
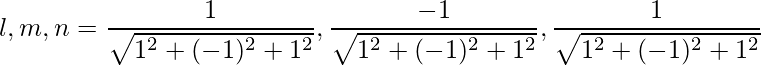
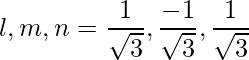
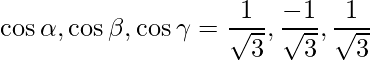
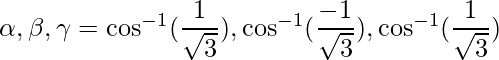
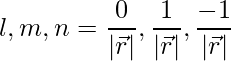
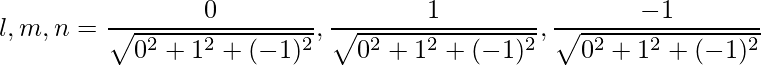
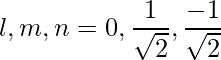
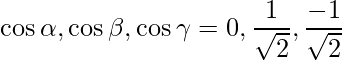
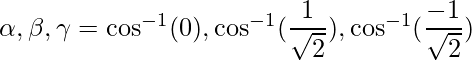
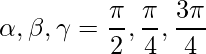
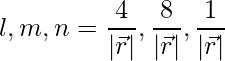
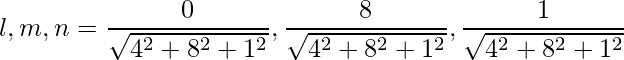
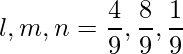
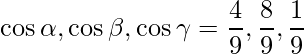
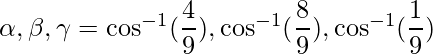
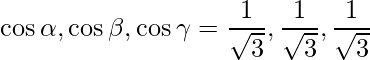
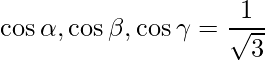
![Rendered by QuickLaTeX.com (\cos \theta)^2 = 1-[\dfrac{1}{2}+\dfrac{1}{4}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6e7c5721bc9b3df9932d5456f3d2448d_l3.png)
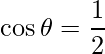
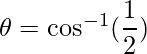
![Rendered by QuickLaTeX.com l^2 =1 - [(\dfrac{1}{\sqrt{2}})^2+(0)^2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7974ed6442dd6f3ae0c7efea13d5b062_l3.png)