Pregunta 17. Si 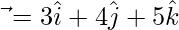 y
y 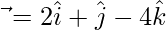 , entonces exprese
, entonces exprese  en la forma
en la forma 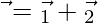 donde
donde 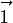 es paralelo a
es paralelo a  y
y 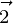 es perpendicular a
es perpendicular a  .
.
Solución:
Dado,
segun pregunta
también
= 0
Ahora,
⇒
⇒
⇒
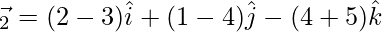
Ahora,
⇒
⇒ 3(2-3λ)+4(1-4λ)-5(4+5λ) = 0
⇒ 6-9λ+4-16λ-20-25λ = 0
⇒ -10 -50λ = 0
⇒ λ = -1/5
Pregunta 18. Si 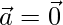 o bien
o bien 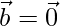 , entonces
, entonces 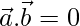 . Pero, lo contrario no tiene por qué ser cierto. Justifica tu respuesta con un ejemplo.
. Pero, lo contrario no tiene por qué ser cierto. Justifica tu respuesta con un ejemplo.
Solución:
Dado,
o
entonces
Suponer
Pero,
= √(2) 2 +(1) 2 +(1) 2
= √4+1+1
= √6 ≠ 0
= √(1) 2 +(1) 2 +(1) 2
= √3 ≠ 0
Por lo tanto probado
Pregunta 19. Demuestra que los vectores 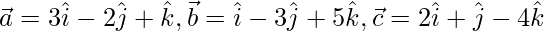 forman un triángulo rectángulo.
forman un triángulo rectángulo.
Solución:
Dado,
Demostrar que los vectores dados forman un triángulo rectángulo
= √(3 2 +(-2) 2 +1 2 ) = √14
= √(1 2 +(-3) 2 +5 2 ) = √35
= √(2 2 +1 2 +(-4) 2 ) = √21
= 14 + 21 = 35
Ya que,
(Teorema de Pitágoras)
Por lo tanto,
y
forman un triángulo rectángulo.
Pregunta 20. Si  ,
, 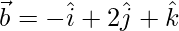 y
y 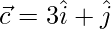 son tales que
son tales que 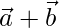 son perpendiculares a
son perpendiculares a 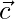 , entonces encuentra el valor de λ.
, entonces encuentra el valor de λ.
Solución:
Dado:
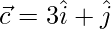
Ahora,
⇒
⇒
⇒ (2 – λ)3 + (2 + 2λ) + 0 = 0
⇒ 6 – 3λ + 2 + 2λ =0
⇒ λ = 8
Pregunta 21. Encuentra los ángulos de un triángulo cuyos vértices son A (0, -1, -2), B (3, 1, 4) y C (5, 7, 1).
Solución:
Dado ese ángulo de un triángulo cuyos vértices son A (0, -1. -2), B (3, 1, 4) y C (5, 7, 1).
= √98 = 7√2
Ahora,
= (3 × 2 + 2 × 6 – 6 × 3) = 0
Por tanto, podemos decir que AB es perpendicular a BC.
Por lo tanto, AB = BC = 7, ∠A =∠C y ∠B = 90°
∠A + ∠B + ∠C = 180°
2∠A = 180° – 90°
∠A = 45°
∠C = 45°
∠B = 90°
Pregunta 22. Halla la magnitud de dos vectores  y
y 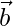 , que tienen la misma magnitud y tales que el ángulo entre ellos es de 60° y su producto escalar es 1/2.
, que tienen la misma magnitud y tales que el ángulo entre ellos es de 60° y su producto escalar es 1/2.
Solución:
Sabemos
⇒ 1/ 2 =
⇒ 1/2 =
(1/2)
⇒
o
⇒
Pregunta 23. Demostrar que los puntos cuyo vector de posición son 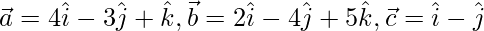 forman un triángulo rectángulo.
forman un triángulo rectángulo.
Solución:
Dado que los vectores de posiciones
Ahora,
⇒
⇒
⇒
Ahora,
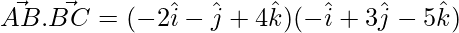
= 2 – 3 – 20 = -21
= -3 – 6 – 5 = -14
= -6 + 2 + 4 = 0
Entonces, AB es perpendicular a CA o los vectores de posición dados forman un triángulo rectángulo.
Pregunta 24. Si los vértices A, B, C de △ABC tienen vectores de posición (1, 2, 3), (-1, 0, 0), (0, 1, 2) respectivamente, ¿cuál es la magnitud de ∠ABC ?
Solución:
Dados los vértices de △ABC son A(1, 2, 3), B(-1, 0, 0), C(0, 1, 2)
Ahora,
=
O,
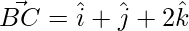
Lo sabemos
(2 × 1) + (2 × 1) + (3 × 2)
= 2 + 2 + 6 = 10
Ahora,
= √17
= √6
Por lo tanto,
cos θ =
porque θ = 10/ √(17×6)
θ = cos -1 (10/√102)
Pregunta 25. Si A, B, C tienen vectores de posición (0, 1, 1), (3, 1, 5), (0, 3, 3) respectivamente, muestra que △ABC es un ángulo recto en C.
Solución:
Dados los vectores de posición A(0, 1, 1), B(3, 1, 5), C(0, 3, 3)
Ahora,
=
= 2 × 2 – 2 × 2 = 0
Por lo tanto,
y
son perpendiculares, por lo tanto, △ABC tiene un ángulo recto en C
Pregunta 26. Encuentra la proyección de  sobre
sobre 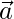 , dónde
, dónde 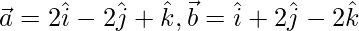 y
y 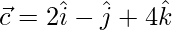 .
.
Solución:
Dado:
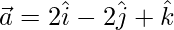
Para encontrar la proyección de
sobre
Ahora, Proyección de
=
=
= 6/9 × 3
= 2
Pregunta 27. Si 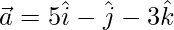 y
y 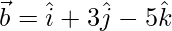 , entonces demuestre que los vectores
, entonces demuestre que los vectores 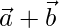 y
y 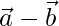 son ortogonales.
son ortogonales.
Solución:
Dado:
Probar
Tomando LHS
=
=
= √35 – √35
= 0
Así, los vectores dados
y
son ortogonales.
Pregunta 28. Un vector unitario  forma un ángulo π/2 y π/3 con
forma un ángulo π/2 y π/3 con 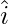 y
y 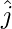 respectivamente y un ángulo agudo θ con
respectivamente y un ángulo agudo θ con 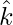 . Encuentre el ángulo θ y las componentes de
. Encuentre el ángulo θ y las componentes de 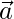 .
.
Solución:
Supongamos
Lo sabemos
un 1 2 + un 2 2 + un 3 2 = 1 ….(1)
Asi que,
(1)(1)(1/√2) = un 1
un 1 = 1/√2
Nuevamente tomamos
(1)(1)(1/2) = un 2
un 2 = 1/2
Ponga todos estos valores en la ecuación (1) para encontrar el valor de un 3
(1/√2) 2 + (1/2) 2 + a 3 2 = 1 ….(1)
un 3 2 = 1/4
un 3 = 1/2
Ahora encontramos el valor de θ
(1)(1)cosθ = 1/2
cosθ = 1/2
cosθ = π/3
y componentes de
Pregunta 29. Si dos vectores  y
y  son tales que
son tales que 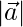 = 2,
= 2, 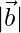 = 1 y
= 1 y 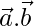 =1. Encuentre el valor de
=1. Encuentre el valor de 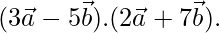
Solución:
Dado,
=
=

= 6(2) 2 + 11(1) – 35(1) 2
= 24 + 11 – 35
= 35 – 35 = 0
Pregunta 30. Si  es un vector unitario, entonces encuentre
es un vector unitario, entonces encuentre 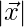 en cada uno de los siguientes:
en cada uno de los siguientes:
(i) 
Solución:
Dado,
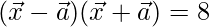
⇒
⇒
⇒
⇒
⇒
(ii) 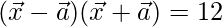
Solución:
Dado,
⇒
⇒
⇒
⇒
⇒
=√13
Pregunta 31. Encuentra 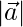 y
y 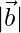 , si
, si
(i) 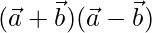 = 12 y
= 12 y 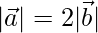
Solución:
Dado,
= 12
⇒
⇒
= 12
⇒
= 12
⇒
= 12
⇒
= 2
Asi que,
= 4
(ii) 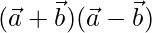 = 8 y
= 8 y 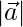 = 8
= 8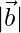
Solución:
Dado,
= 8
⇒
⇒
⇒
⇒
⇒
= √(8/63)
Asi que,
= 8√(8/63)
(iii)  = 3 y
= 3 y 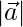 = 2
= 2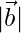
Solución:
Dado,
⇒
⇒
⇒
⇒ 3
= 3
⇒
= 1
Asi que,
= 2
Pregunta 32. Halla  , si
, si
(yo) 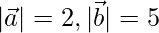 y
y 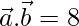
Solución:
Tenemos,
⇒
⇒
= 2 2 – 2 × 8 + 5 2
⇒
= 4 – 16 + 25
⇒
= 13
⇒
= √13
(ii) 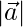 = 3,
= 3, 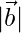 = 4 y
= 4 y 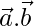 = 1
= 1
Solución:
Tenemos,
⇒
⇒
= 3 2 – 2 × 1 + 4 2
⇒
= 9 – 2 + 16
⇒
= 23
⇒
= √23
(iii)  y
y 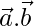 = 4
= 4
Solución:
Tenemos,
⇒
⇒
= 2 2 – 2 × 4 + 3 2
⇒
= 4 – 8 + 9
⇒
= 5
⇒
= √5
Publicación traducida automáticamente
Artículo escrito por rahulsharma1771996 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA