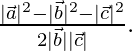Pregunta 33. Encuentra el ángulo entre los dos vectores  y
y 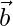 , si
, si
(i) 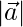 =√3,
=√3, 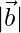 = 2 y
= 2 y 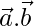 = √6
= √6
Solución:
Sabemos,
⇒ √6 = 2√3 cos θ
⇒ cos θ = 1/√2
⇒ θ = cos -1 (1/√2)
⇒ θ = π/4
(ii) 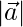 = 3,
= 3, 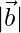 = 3 y
= 3 y 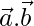 = 1
= 1
Solución:
Sabemos,
⇒ 1 = 3×3 cos θ
⇒ cos θ = 1/9
⇒ θ = cos -1 (1/9)
Pregunta 34. Expresar el vector 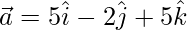 como la suma de dos vectores tales que uno es paralelo al vector
como la suma de dos vectores tales que uno es paralelo al vector 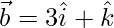 y el otro es perpendicular a
y el otro es perpendicular a 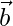
Solución:
Dado,
Sean los dos vectores
Ahora,
….(1)
Suponiendo
que es paralelo a
Entonces,
……(2)
es perpendicular a
Entonces,
……(3)
De la ecuación (1)
⇒
⇒
⇒
De la ecuación (3)
⇒
⇒ (5-3λ)3+(5-λ)=0
⇒ 15-9λ+5-λ=0
⇒ -10λ = -20
⇒ λ=2
De la ecuación (2)
Pregunta 35. Si 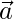 y
y 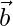 son dos vectores de la misma magnitud inclinados en un ángulo de 30° tal que
son dos vectores de la misma magnitud inclinados en un ángulo de 30° tal que 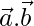 = 3, encuentre
= 3, encuentre 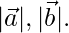
Solución:
Dado que dos vectores de la misma magnitud inclinados en un ángulo de 30°, y
Encontrar
Sabemos,
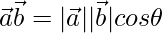
⇒ 3 =
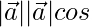
⇒ 3 =
⇒ 3 =
(√3/2)
⇒
= 6/√3
⇒
Pregunta 36. Expresar 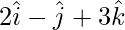 como la suma de un vector paralelo y un vector perpendicular a
como la suma de un vector paralelo y un vector perpendicular a 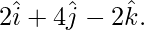
Solución:
Asumiendo
Sean los dos vectores
Ahora,
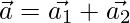
o
….(1)
Suponiendo
que es paralelo a
entonces,
…(2)
es perpendicular a
entonces,
……(3)
Poniendo eq(2) en eq(1), obtenemos
⇒
⇒
⇒
De la ecuación (3)
⇒
⇒ (2 – 2λ)2 – (1 + 4λ)4 – (3 + 2λ)2 = 0
⇒ 4 – 4λ – 4 – 16λ – 6 – 4λ = 0
⇒ 24λ = -6
⇒ λ = -6/24
De la ecuación (2)
Pregunta 37. Descomponer el vector 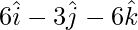 en vectores paralelos y perpendiculares al vector .
en vectores paralelos y perpendiculares al vector .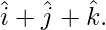
Solución:
dejar
y
Sea
un vector paralelo a
Por lo tanto,
a descomponer en dos vectores
⇒
⇒
Ahora,
es perpendicular a
o
⇒
⇒ 6 – λ – 3 – λ – 6 – λ = 0
⇒ λ = -1
Por lo tanto, los vectores requeridos son
y
Pregunta 38. Sea 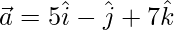 y
y 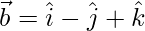 . Encuentre λ tal que
. Encuentre λ tal que 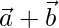 sea ortogonal a
sea ortogonal a 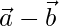
Solución:
Dado,
segun pregunta
⇒
⇒
⇒
⇒ 25 + 1 + 49 = 1 + 1 + λ 2
⇒ λ2 = 73
⇒ λ = √73
Pregunta 39. Si 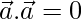 y
y 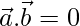 , ¿qué puedes concluir sobre el vector
, ¿qué puedes concluir sobre el vector 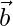 ?
?
Solución:
Dado,
,
Ahora,
Concluimos que
o
o θ = 90°
Por lo tanto,
puede ser cualquier vector arbitrario.
Pregunta 40. Si 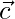 es perpendicular a ambos
es perpendicular a ambos 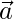 y
y 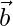 , entonces demuestre que es perpendicular a ambos
, entonces demuestre que es perpendicular a ambos 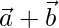 y
y 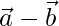
Solución:
Dado
es perpendicular a ambos
y
….(1)
….(2)
para probar
y
Ahora,
⇒
[De la ecuación (1) y (2)]
Otra vez,
⇒
[De la ecuación (1) y (2)]
Por lo tanto probado
Pregunta 41. Si 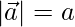 y
y 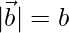 , demuestre que
, demuestre que 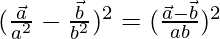
Solución:
dado,
y
Probar
Tomando LHS
=
=
=
Tomando RHS
=
=
LHS = RHS
Por lo tanto probado
Pregunta 42. Si 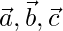 son tres vectores no coplanares tales que
son tres vectores no coplanares tales que 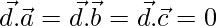 entonces muestre que
entonces muestre que 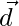 es el vector nulo.
es el vector nulo.
Solución:
Dado que
Así que
o bien
Similarmente,
O bien
o
También,
Entonces
o
Pero
no puede ser perpendicular a
y
porque
no son coplanares.
Entonces
= 0 o
es un vector nulo
Pregunta 43. Si un vector  es perpendicular a dos vectores no colineales
es perpendicular a dos vectores no colineales  y
y 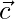 , entonces es
, entonces es  perpendicular a todo vector en el plano de
perpendicular a todo vector en el plano de  y
y 
Solución:
Dado que
es perpendicular a
y
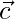
Sea
cualquier vector en el plano de
y
y
es la combinación lineal de
y

[x, y son escalares]
Ahora
⇒
⇒
⇒
⇒
Por lo tanto,
es perpendicular a es
decir ,
es perpendicular a todo vector.
Pregunta 44. Si 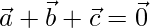 , ¿cómo es que el ángulo θ entre los vectores
, ¿cómo es que el ángulo θ entre los vectores 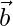 y
y 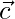 está dado por cos θ =
está dado por cos θ = 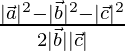
Solución:
Dado que
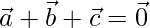
⇒
⇒
⇒
⇒
⇒
⇒
⇒ cos θ =
Pregunta 45. Sea 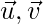 y
y 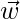 sea vector tal
sea vector tal 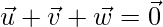 .
. 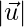 = 3,
= 3, 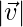 = 4 y
= 4 y 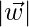 = 5, luego encuentra
= 5, luego encuentra 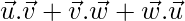
Solución:
Dado que
y
son vectores tales que
.
= 3,
= 4 y
=5,
Encontrar
Tomando
Cuadrando en ambos lados, obtenemos
⇒
⇒
⇒
⇒
⇒
Por lo tanto,
Pregunta 46. Sean 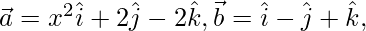 y
y 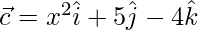 tres vectores. Encuentre los valores de x para los cuales el ángulo entre
tres vectores. Encuentre los valores de x para los cuales el ángulo entre  y
y  es agudo y el ángulo entre
es agudo y el ángulo entre  y
y  es obtuso.
es obtuso.
Solución:
Dado
Caso I: Cuando el ángulo entre
y
es agudo:-
>0
⇒
⇒ x 2 – 2 – 2 > 0
⇒x2 > 4
x ∈ (2, -2)
Caso II: Cuando el ángulo entre
y
es obtuso:-
⇒
⇒ x 2 – 5 – 4 < 0
⇒x2 < 9
x ∈ (3, -3)
Por lo tanto, x ∈ (-3, -2)∪(2, 3)
Pregunta 47. Encuentra el valor de x e y si los vectores 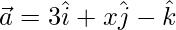 y
y 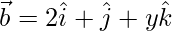 son vectores mutuamente perpendiculares de igual magnitud.
son vectores mutuamente perpendiculares de igual magnitud.
Solución:
Dados
son vectores mutuamente perpendiculares de igual magnitud.
⇒ 3 2 + x 2 + (-1) 2 = 2 2 + 1 2 + y 2
⇒ x 2 + 10 = y 2 + 5
⇒ x2 – y2 + 5 = 0 ….(1)
Ahora,
⇒ 6 + x – y = 0
⇒ y = x + 6 …..(2)
De la ecuación (1)
x 2 – (x + 6) 2 + 5 = 0
⇒ x2 – (x2 + 36 – 12x) + 5 = 0
⇒ -12x – 31 = 0
⇒ x = -31/12
Ahora, y = -31/12 + 6
y = 41/12
Pregunta 48. Si  y
y  son dos vectores unitarios no coplanares tales que
son dos vectores unitarios no coplanares tales que 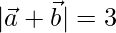 , hallar
, hallar 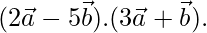
Solución:
Dado que
y
son dos vectores unitarios no coplanares tales que
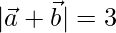
Encontrar
Ahora,
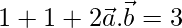
Ahora,
=
= 6 – 13(1/2) – 5
= 1 – 13/2
= -11/2
Pregunta 49. Si 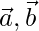 son dos vectores tales que |
son dos vectores tales que | 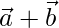 | =
| = 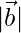 , luego demuestre que
, luego demuestre que 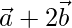 es perpendicular a
es perpendicular a 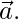
Solución:
Probar
Ahora,
Cuadrando en ambos lados, obtenemos
⇒
⇒
⇒
⇒
Por lo tanto,
es perpendicular a
Publicación traducida automáticamente
Artículo escrito por rahulsharma1771996 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA