Clase 12 Soluciones RD Sharma – Capítulo 24 Producto Escalar o Punto – Ejercicio 24.2

Pregunta 1. En un triángulo OAB, si P, Q son puntos de trisección de AB, Demostrar que OP ² + OQ ² = 5/9 AB ² .

Solución:

Dado que en el triángulo OAB,

∠AOB = 90°, y P, Q son puntos de trisección de AB.

Considere ‘O’ como origen, los vectores de posición de A y B son $\vec{a}$ y $\vec{b}$ respectivamente.

Como P y Q son puntos de trisección de AB, AP:PB = 1:2 y AQ:QB = 2:1.

De la fórmula de la sección, el vector de posición de P es $\vec{OP}=\frac{2\vec{a}+\vec{b}}{3}$

El vector de posición de Q es $\vec{OQ}=\frac{\vec{a}+2\vec{b}}{3}$

Ahora, OP ² + OQ ² = $|\overrightarrow{OP}|^2+|\overrightarrow{OQ}|^2$

⇒ $(\frac{2\vec{a}+\vec{b}}{3}).(\frac{2\vec{a}+\vec{b}}{3})+(\frac{\vec{a}+2\vec{b}}{3}).(\frac{\vec{a}+2\vec{b}}{3})$

⇒ $\frac{4|\vec{a}|^2+4\vec{a}.\vec{b}+|\vec{b}|^2+|\vec{a}|^2+4\vec{a}.\vec{b}+4|\vec{b}|^2}{9}$

Sabemos que $\vec{a}.\vec{b}=0$ , ya que $\vec{a}$ y $\vec{b}$ son perpendiculares.

⇒ $\frac{5}{9}[|\vec{a}|^2+|\vec{b}|^2]$

Usando el teorema de Pitágoras, obtenemos

$\frac{5}{9}|\overrightarrow{AB}|^2$

Por lo tanto probado.

Pregunta 2. Demuestra que si las diagonales de un cuadrilátero se bisecan en ángulo recto, entonces es un rombo.

Solución:

Consideremos que OABC es un cuadrilátero y las diagonales AB y OC se bisecan a 90°.

Considere ‘0’ como origen y los vectores de posición de A y B están dados por $\vec{a}$ y $\vec{b}$ respectivamente.

Ahora, el vector de posición de E es $\overrightarrow{OE}=\frac{\vec{a}+\vec{b}}{2}$

Usando la ley del triángulo de la suma de vectores, $\overrightarrow{OB}=\overrightarrow{OA}+\overrightarrow{AB}$

⇒ $\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}$

⇒ $\overrightarrow{AB}=\vec{b}-\vec{a}$

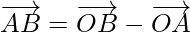
Como las diagonales se bisecan a 90°, $\vec{AB}.\vec{OC}=0$

⇒ $(\vec{b}-\vec{a}).(\vec{b}-\vec{a})=0$

⇒ $|\vec{b}|^2-|\vec{a}|^2=0$

⇒ |

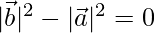
⇒OA = OB

Por lo tanto, probamos que los lados adyacentes del cuadrilátero son iguales si sus diagonales se bisecan a 90°.

Pregunta 3. Demostrar por el método vectorial que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados (Teorema de Pitágoras).

Solución:

Consideremos que ABC es el triángulo rectángulo con ∠BAC = 90°.

Considere ‘A’ como origen y los vectores de posición $AB=\vec{b},AC=\vec{c}$

Como AB y AC son perpendiculares entre sí, $\vec{a}.\vec{b}=0$

Ahora, AB ² + AC ² = $|\vec{b}|^2+|\vec{c}|^2$ …(1)

De la ley del triángulo de la suma de vectores, $\overrightarrow{AC}^2=\overrightarrow{AB}^2+\overrightarrow{BC}^2$

⇒ $\overrightarrow{BC}^2=\overrightarrow{AC}^2-\overrightarrow{AB}^2$

⇒ $\overrightarrow{BC}^2=\vec{c}^2-\vec{b}^2$

Ahora, BC ² = $|\overrightarrow{BC}|^2=|\vec{c}-\vec{b}|^2$

⇒ $(\vec{c}-\vec{b}).(\vec{c}-\vec{b})$

⇒ $|\vec{c}|^2+|\vec{b}|^2-2\vec{c}.\vec{b}$

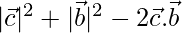
⇒ $|\vec{c}|^2+|\vec{b}|^2$ …(2)

Por lo tanto, de eq(1) y eq(2) obtenemos,

⇒

Por lo tanto probado.

Pregunta 4. Demostrar por el método vectorial que la suma de los cuadrados de las diagonales del paralelogramo es igual a la suma de los cuadrados de sus lados.

Solución:

Consideremos ABCD como un paralelogramo y AC, BD como sus diagonales.

Considere A como origen, Deje que los vectores de posición de AB, AD sean $\vec{b},\vec{d}$ respectivamente.

Usando la ley del triángulo de la suma de vectores, tenemos $\overrightarrow{AD}+\overrightarrow{DB}=\overrightarrow{AB}$

⇒ $\overrightarrow{DB}=\overrightarrow{AB}-\overrightarrow{AD}$

⇒ $\overrightarrow{DB}=\vec{b}-\vec{d}$

En el triángulo ABC,

$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}=\vec{b}+\vec{d}$

Ahora, cuadrados de lados del paralelogramo =

⇒ $|\overrightarrow{AD}|^2+|\overrightarrow{AB}|^2+|\overrightarrow{-AB}|^2+|-\overrightarrow{AD}|^2$

⇒ $2|\overrightarrow{AB}|^2+2|\overrightarrow{AD}|^2$

⇒ $2|\vec{b}|^2+2|\vec{d}|^2$ …(1)

Además, cuadrados de diagonales =

⇒ $|\overrightarrow{DB}|^2+|\overrightarrow{AC}|^2$

⇒ $|\vec{b}|^2-2\vec{b}.\vec{d}+|\vec{d}|^2+|\vec{b}|^2+2\vec{b}.\vec{d}+|\vec{d}|^2$

⇒ $2|\vec{b}|^2+2|\vec{d}|^2$ …(2)

Por, observando eq(1) y eq(2),

Probamos que la suma de los cuadrados de los lados de un paralelogramo es igual a la suma de los cuadrados de sus diagonales.

Pregunta 5. Demostrar mediante el método vectorial que el cuadrilátero obtenido al unir los puntos medios de los lados adyacentes del rectángulo es un rombo.

Solución:

Consideremos que ABCD es un rectángulo y P, Q, R, S son puntos medios de AB, BC, CD, DA respectivamente.

Considere A como origen, los vectores de posición de AB, AD son $\vec{b},\vec{d}$ respectivamente.

Ahora, usando la ley del triángulo de la suma de vectores, $\overrightarrow{PQ}=\overrightarrow{PB}+\overrightarrow{BQ}$

⇒ $\frac{\overrightarrow{AB}}{2}+\frac{\overrightarrow{BC}}{2}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{BC})$

⇒ $\overrightarrow{PQ}=\frac{1}{2}(\overrightarrow{AC})$

Similarmente,

$\overrightarrow{SR}=\overrightarrow{SD}+\overrightarrow{DR}$

⇒ $\frac{\overrightarrow{AD}}{2}+\frac{\overrightarrow{DC}}{2}=\frac{1}{2}(\overrightarrow{AD}+\overrightarrow{DC})$

⇒ $\overrightarrow{SR}=\frac{1}{2}(\overrightarrow{AC})$

Al observar, encontramos que PQ || SR, entonces podemos decir que es un paralelogramo

Hallemos si forma un rombo calculando la longitud de los lados adyacentes,

⇒ $|\overrightarrow{PQ}|^2=\frac{1}{4}|\overrightarrow{AC}|^2$ …(1)

También, de la figura, $\overrightarrow{PS}=\overrightarrow{AS}-\overrightarrow{PA}$

⇒ $\frac{\overrightarrow{AD}}{2}-\frac{-\overrightarrow{AB}}{2}=\frac{1}{2}(\overrightarrow{AD}+\overrightarrow{AB})$

⇒ $\overrightarrow{PS}=\frac{1}{2}(\overrightarrow{AC})$

⇒ $|\overrightarrow{PS}|^2=\frac{1}{4}(|\overrightarrow{AC}|^2)$ …(2)

De eq(1) y eq(2) PQ y PS son lados adyacentes y |PQ|=|PS|,

entonces PQRS es un rombo.

Por lo tanto, Por lo tanto demostrado

Pregunta 6. Demuestra que las diagonales de un rombo son bisectrices perpendiculares entre sí.

Solución:

Consideremos que OABC es un rombo, OB y AC son diagonales de rombo.

Considere O como origen, los vectores de posición de OA y OC son $\vec{a},\vec{c}$ respectivamente.

De figura, $\overrightarrow{OB} = \overrightarrow{OA}+\overrightarrow{AB}$

⇒ $\overrightarrow{OB} = \vec{a}+\vec{c}$

De figura, $\overrightarrow{OC} = \overrightarrow{OA}+\overrightarrow{AC}$

⇒ $\overrightarrow{AC} = \vec{c}-\vec{a}$

Ahora, $\overrightarrow{OB}.\overrightarrow{AC}=(\vec{c}+\vec{a}).(\vec{c}-\vec{a})$

⇒ $|\vec{c}|^2-|\vec{a}|^2$

Sabemos que los lados adyacentes son iguales en un rombo,

⇒ $\overrightarrow{OB}.\overrightarrow{AC}=|\vec{c}|^2-|\vec{a}|^2=0$

Por lo tanto, las diagonales de un rombo son bisectrices perpendiculares entre sí.

Pregunta 7. Demuestra que las diagonales del rectángulo son perpendiculares si y solo si el rectángulo es un cuadrado.

Solución:

Consideremos que ABCD es un rectángulo, AC, BD son diagonales del rectángulo.

Considere A como origen, los vectores de posición de AB, AD son $\vec{b},\vec{d}$ respectivamente.

De figura, $\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}$

⇒ $\overrightarrow{AC}=\vec{b}+\vec{d}$

Similarmente, $\vec{AD}=\vec{AB}+\vec{BD}$

⇒ $\overrightarrow{BD}=\vec{d}-\vec{b}$

Si las diagonales son perpendiculares, entonces $\overrightarrow{AC}.\overrightarrow{BD}=0$

⇒ $(\vec{b}+\vec{d}).(\vec{b}-\vec{d})=0$

⇒ $|\vec{b}|^2-|\vec{d}|^2=0$

⇒ $|\vec{b}|=|\vec{d}|$

Por lo tanto, si las diagonales de un rectángulo son perpendiculares, entonces es un cuadrado.

Pregunta 8. Si AD es la mediana del triángulo ABC, prueba con vectores que

Solución:

Consideremos que ABC es un triángulo y AD es una mediana.

Considere que A es un origen, los vectores de posición de AB y AC lo son $\vec{b},\vec{c}$ respectivamente.

El vector de posición de AD es $\overrightarrow{AD}=\frac{\vec{b}+\vec{c}}{2}$

El vector de posición de CD es $\overrightarrow{CD}=\overrightarrow{AD}-\overrightarrow{AC}$

⇒ $\overrightarrow{CD}=\frac{\vec{b}+\vec{c}}{2}-\vec{c}=\frac{\vec{b}-\vec{c}}{2}$

Ahora, AB ² + AC ² = $|\overrightarrow{AB}|^2+|\overrightarrow{AC}|^2=|\vec{b}|^2+|\vec{c}|^2$ …(1)

Además, 2(AD ² + CD ² ) = $2(|\vec{AD}|^2+|\vec{CD}|^2)$

⇒ $2(\frac{|\vec{b}|^2+|\vec{c}|^2+2\vec{b}.\vec{c}}{2}+\frac{|\vec{b}|^2+|\vec{c}|^2-2\vec{b}.\vec{c}}{2})$

⇒ $|\vec{b}|^2+|\vec{c}|^2$ …(2)

De eq(1) y eq(2), obtenemos

Por lo tanto, Por lo tanto probado.

Pregunta 9. Si la mediana a la base del triángulo es perpendicular a la base, entonces el triángulo es isósceles.

Solución:

Consideremos que ABC es un triángulo y AD es una mediana.

Considere A como origen, el vector de posición de AB, AC son $\vec{b},\vec{c}$ respectivamente.

Ahora, el vector de posición de AD es $\overrightarrow{AD}=\frac{\vec{b}+\vec{c}}{2}$

Usando la ley del triángulo de la suma de vectores, $\overrightarrow{AC}=\overrightarrow{BC}+\overrightarrow{AB}$

⇒ $\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}=\vec{c}-\vec{b}$

Como AD y BC son perpendiculares, $\overrightarrow{BC}.\overrightarrow{AD}=0$

⇒ $(\vec{c}-\vec{b}).\frac{\vec{b}+\vec{c}}{2}=0$

⇒ $(\vec{c}-\vec{b}).(\vec{c}+\vec{b})=0$

⇒ $|\vec{c}|^2-|\vec{b}|^2=0$

⇒ $|\vec{c}|=|\vec{b}|$

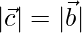
⇒ CA = AB

Por lo tanto, el Triángulo ABC es un triángulo Isósceles.

Pregunta 10. En un cuadrilátero ABCD, demostrar que , donde P, Q son puntos medios de las diagonales AC y BD.

Solución:

Consideremos que ABCD es un cuadrilátero, AC, BD son diagonales.

Considere A como origen, los vectores de posición de AB, AC, AD son $\vec{b},\vec{c},\vec{d}$ respectivamente.

Sean P y Q los puntos medios de AC, BD.

El vector de posición de P es $\frac{\overrightarrow{AC}}{2}=\frac{\vec{c}}{2}$

El vector de posición de Q es $\frac{\vec{b}+\vec{d}}{2}$

Ahora, AB ² + BC ² + CD ² + DA ² = $|\overrightarrow{AB}|^2+|\overrightarrow{BC}|^2+|\overrightarrow{CD}|^2+|\overrightarrow{DA}|^2$

⇒ $|\vec{b}|^2+|\vec{c}-\vec{b}|^2+|\vec{d}-\vec{c}|^2+|\vec{d}|^2$

⇒ $2|\vec{b}|^2+2|\vec{c}|^2+2|\vec{d}|^2-2\vec{b}.\vec{c}-2\vec{c}.\vec{d}$ …(1)

Además, AC ² + BD ² + 4PQ ² = $|\overrightarrow{AC}|^2+|\overrightarrow{BD}|^2+4|\overrightarrow{PQ}|^2$

⇒ $|\vec{c}|^2+|\vec{d}-\vec{b}|^2+4|\frac{|\vec{b}+\vec{d}|^2}{2}-\frac{|\vec{c}|^2}{2}|^2$

⇒ $|\vec{c}|^2+|\vec{d}-\vec{b}|^2+|\vec{b}+\vec{d}|^2-2|\vec{b}+\vec{d}|.|\vec{c}|+|\vec{c}|^2$

⇒ $2|\vec{b}|^2+2|\vec{c}|^2+2|\vec{d}|^2-2\vec{b}.\vec{c}-2\vec{c}.\vec{d}$ …(2)

De eq(1) y eq(2), obtenemos,

Por lo tanto, Por lo tanto probado.

Publicación traducida automáticamente

Artículo escrito por srinivasteja18 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. En un triángulo OAB, si P, Q son puntos de trisección de AB, Demostrar que OP 2 + OQ 2 = 5/9 AB 2 .

Pregunta 2. Demuestra que si las diagonales de un cuadrilátero se bisecan en ángulo recto, entonces es un rombo.

Pregunta 3. Demostrar por el método vectorial que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados (Teorema de Pitágoras).

Pregunta 4. Demostrar por el método vectorial que la suma de los cuadrados de las diagonales del paralelogramo es igual a la suma de los cuadrados de sus lados.

Pregunta 5. Demostrar mediante el método vectorial que el cuadrilátero obtenido al unir los puntos medios de los lados adyacentes del rectángulo es un rombo.

Pregunta 6. Demuestra que las diagonales de un rombo son bisectrices perpendiculares entre sí.

Pregunta 7. Demuestra que las diagonales del rectángulo son perpendiculares si y solo si el rectángulo es un cuadrado.

Pregunta 8. Si AD es la mediana del triángulo ABC, prueba con vectores que

Pregunta 9. Si la mediana a la base del triángulo es perpendicular a la base, entonces el triángulo es isósceles.

Pregunta 10. En un cuadrilátero ABCD, demostrar que , donde P, Q son puntos medios de las diagonales AC y BD.

Deja una respuesta Cancelar la respuesta

Pregunta 1. En un triángulo OAB, si P, Q son puntos de trisección de AB, Demostrar que OP ² + OQ ² = 5/9 AB ² .