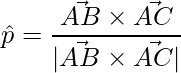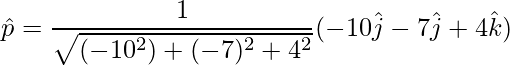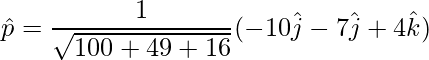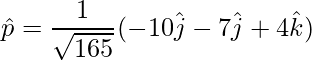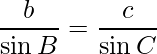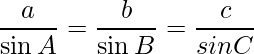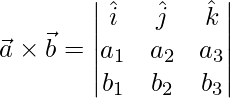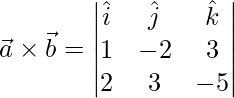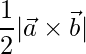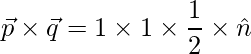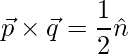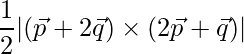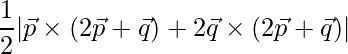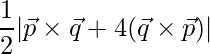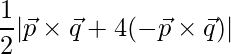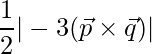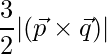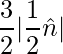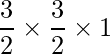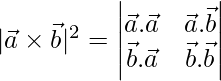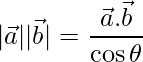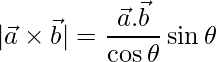Pregunta 13. Si 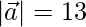 ,
, 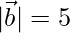 y
y 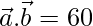 , encuentran
, encuentran 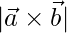
Solución:
Lo sabemos,
=>
=>
=>
=>
=>
También,
=>
Y
=>
=>
=>
=>
=>
=>
Pregunta 14. Encuentra el ángulo entre 2 vectores  y
y 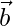 , si
, si 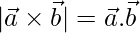
Solución:
Dado
=>
=>
, como
es un vector unitario.
=>
=>
=>
Pregunta 15. Si 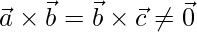 , entonces demuestre que
, entonces demuestre que 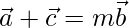 , donde m es cualquier escalar.
, donde m es cualquier escalar.
Solución:
Dado que
=>
=>
=>
Usando la propiedad distributiva,
=>
Si dos vectores son paralelos, entonces su producto vectorial es 0 vector.
=>
y
son vectores paralelos.
=>
Por lo tanto probado.
Pregunta 16. Si 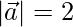 ,
, 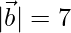 y
y 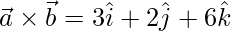 , encuentra el ángulo entre
, encuentra el ángulo entre  y
y 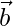
Solución:
Dado que
,
y
Lo sabemos,
=>
=>
=>
=>
=>
=>
=>
=>
Pregunta 17. ¿Qué inferencia puedes sacar si 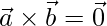 y
y 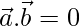
Solución:
dado,
y
=>
=>
Cualquiera de las siguientes condiciones es verdadera,
1.
2.
3.
4.
es paralelo a
=>
=>
Cualquiera de las siguientes condiciones es verdadera,
1.
2.
3.
4.
es perpendicular a
Dado que ambas condiciones son verdaderas, eso implica que al menos una de las siguientes condiciones es verdadera,
1.
2.
3.
Pregunta 18. Si  ,
,  y
y 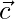 son 3 vectores unitarios tales que
son 3 vectores unitarios tales que 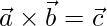 ,
, 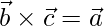 y
y 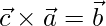 . Demuestre que
. Demuestre que  ,
, 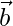 y
y 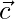 forme una tríada ortogonal derecha de vectores unitarios.
forme una tríada ortogonal derecha de vectores unitarios.
Solución:
Dado
,
y
Como,
=>
=>
es perpendicular a ambos
y
.
Similarmente,
=>
es perpendicular a ambos
y
=>
es perpendicular a ambos
y
=>
,
y
son mutuamente perpendiculares.
Como,
,
y
también son vectores unitarios,
=>
,
y
forman una tríada ortogonal dextrógira de vectores unitarios
Por lo tanto probado.
Pregunta 19. Encuentra un vector unitario perpendicular al plano ABC, donde las coordenadas de A, B y C son A(3, -1, 2), B(1, -1, 3) y C(4, – 3, 1).
Solución:
Dados A(3, -1, 2), B(1, -1, 3) y C(4, -3, 1).
Dejar,
=>
=>
=>
El plano ABC tiene dos vectores
y
=>
=>
=>
=>
=>
=>
=>
=>
Un vector perpendicular a ambos
y
viene dado por,
=>
=>
=>
=>
=>
Para encontrar el vector unitario,
=>
=>
=>
=>
Pregunta 20. Si a, b y c son las longitudes de los lados BC, CA y AB de un triángulo ABC, demuéstralo 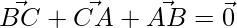 y deduce que
y deduce que 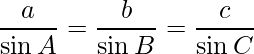
Solución:
Dado eso
,
y
De la ley del triángulo de la suma de vectores, tenemos
=>
=>
=>
=>
=>
=>
=>
=>
=>
=>
=>
=>
=>
=>
=>
Similarmente,
=>
=>
=>
=>
=>
=>
=>
=>
=>
=>
=>
Por lo tanto probado.
Pregunta 21. Si 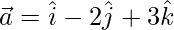 y
y 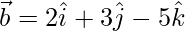 , entonces encuentra
, entonces encuentra  . Compruebe que
. Compruebe que 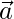 y
y  son perpendiculares entre sí.
son perpendiculares entre sí.
Solución:
dado,
y
=>
=>
=>
=>
=>
Dos vectores son perpendiculares si su producto escalar es cero.
=>
=>
=>
=>
Por lo tanto probado.
Pregunta 22. Si 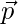 y
y 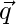 son vectores unitarios que forman un ángulo de
son vectores unitarios que forman un ángulo de 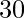 , encuentre el área del paralelogramo que tiene
, encuentre el área del paralelogramo que tiene 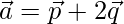 y
y 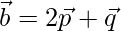 como sus diagonales.
como sus diagonales.
Solución:
Dado
y
formando un ángulo de
.
Área de un paralelogramo que tiene diagonales
y
es
=>
=>
=>
Así el área es,
=> Área =
=> Área =
=> Área =
=> Área =
=> Área =
=> Área =
=> Área =
=> Área =
=> Área =
unidades cuadradas
Pregunta 23. Para cualesquiera dos vectores 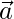 y
y 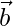 , demuestre que
, demuestre que 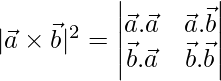
Solución:
Lo sabemos,
=>
=>
=>
=>
=>
=>
=>
=>
=>
Por lo tanto probado.
Pregunta 24. Defina  y demuestre que
y demuestre que 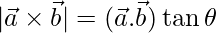 , ¿dónde
, ¿dónde 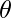 está el ángulo entre
está el ángulo entre 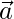 y
y 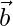
Solución:
Definición de : Sean y sean 2 vectores distintos de cero, no paralelos. Entonces , se define como un vector con la magnitud de , y que es perpendicular tanto a los vectores como a .
Lo sabemos,
=>
=>
=>
……………..(ecuación 1)
Y como,
=>
=>
Sustituyendo en (eq.1),
=>
=>
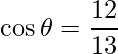
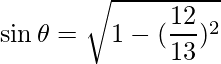
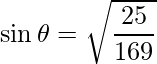
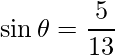
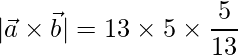
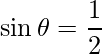
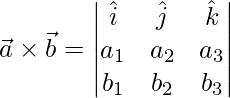
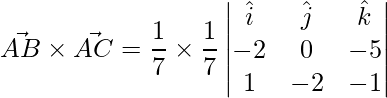
![Rendered by QuickLaTeX.com \vec{AB}\times\vec{AC} = \hat{i}[(0)(-1)-(-2)(-5)] -\hat{j}[(-2)(-1)-(1)(-5)] +\hat{k}[(-2)(-2)-(1)(0)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5ca884f9c9d7761da4ced643aa6267fa_l3.png)