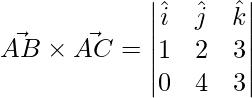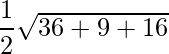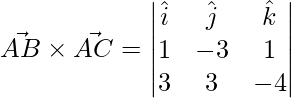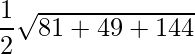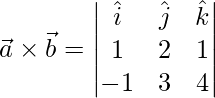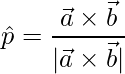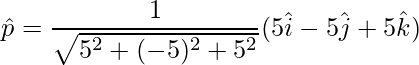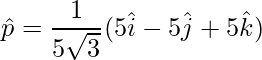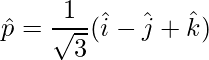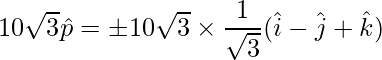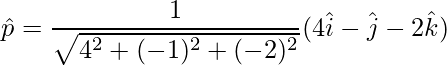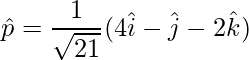Pregunta 25. Si 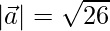 ,
, 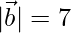 y
y 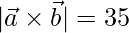 , encuentran
, encuentran 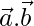
Solución:
Lo sabemos,
=>
=>
=>
=>
=>
como
,
=>
=>
=>
=>
De este modo,
=>
=>
=>
Pregunta 26. Encuentra el área del triángulo formado por O, A, B cuando 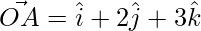 ,
, 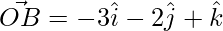
Solución:
El área de un triángulo cuyos lados adyacentes están dados por
y
es
=>
=>
=>
=>
=> Área =
=> Área =
=> Área =
=> Área =
=> Área =
unidades cuadradas.
Pregunta 27. Sea 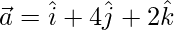 ,
, 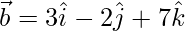 y
y 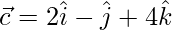 . Encuentre un vector
. Encuentre un vector 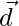 que sea perpendicular a ambos
que sea perpendicular a ambos 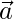 y
y 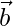 y
y 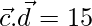
Solución:
Dado que
es perpendicular a ambos
y
.
=>
……….(1)
=>
……….(2)
También,
=>
…….(3)
Dejar
De la ecuación (1),
=> re 1 + 4 re 2 + 2 re 3 = 0
De la ecuación (2),
=> 3 días 1 – 2 días 2 + 7 días 3 = 0
De la ecuación (3),
=> 2d 1 – re 2 + 4d 3 = 15
Al resolver las 3 ecuaciones obtenemos,
d 1 = 160/3, d 2 = -5/3 y d 3 = -70/3,
=>
Pregunta 28. Encuentra un vector unitario perpendicular a cada uno de los vectores 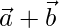 y
y 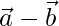 , donde
, donde 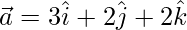 y
y 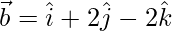 .
.
Solución:
Dado eso,
y
Dejar
=>
=>
=>
Dejar
=>
=>
=>
Un vector perpendicular a ambos
y
es,
=>
=>
=>
=>
Para encontrar el vector unitario,
=>
=>
=>
=>
=>
Pregunta 29. Usando vectores, encuentra el área del triángulo con los vértices A(2, 3, 5), B(3, 5, 8) y C(2, 7, 8).
Solución:
Dado, A(2, 3, 5), B(3, 5, 8) y C(2, 7, 8)
Dejar,
=>
=>
=>
Después,
=>
=>
=>
=>
=>
=>
=>
=>
El área de un triángulo cuyos lados adyacentes están dados por
y
es
=>
=>
=>
=> Área =
=> Área =
=> Área = √61/2
Pregunta 30. Si 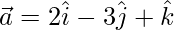 ,
, 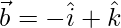 ,
, 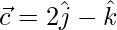 son tres vectores, encuentra el área del paralelogramo que tiene las diagonales
son tres vectores, encuentra el área del paralelogramo que tiene las diagonales 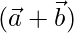 y
y 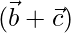 .
.
Solución:
Dado,
,
,
Dejar,
=>
=>
=>
=>
=>
=>
=>
El área del paralelogramo que tiene diagonales
y
es
=>
=>
=>
=> Área =
=> Área =
=> Área =
=> Área = √21/2
Pregunta 31. Los dos lados adyacentes de un paralelogramo son 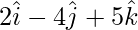 y
y 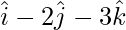 . Encuentra el vector unitario paralelo a una de sus diagonales. Además, encuentre su área.
. Encuentra el vector unitario paralelo a una de sus diagonales. Además, encuentre su área.
Solución:
Dado un paralelogramo ABCD y sus 2 lados AB y BC.
Por la ley triangular de la suma,
=>
=>
=>
=>
vector unitario es,
=>
=>
=>
=>
El área de un paralelogramo cuyos lados adyacentes se dan es
=>
=>
=>
Así el área es,
=> Área =
=> Área =
=> Área =
=> Área = 11 √5 unidades cuadradas
Pregunta 32. Si 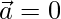 o bien
o bien 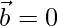 , entonces
, entonces 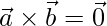 . ¿Es cierto lo contrario? Justifique con el ejemplo.
. ¿Es cierto lo contrario? Justifique con el ejemplo.
Solución:
Tomemos dos vectores paralelos distintos de cero
y
=>
Por ejemplo,
y
=>
=>
Pero,
=>
=>
Por lo tanto, lo contrario puede no ser cierto.
Pregunta 33. Si 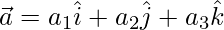 ,
, 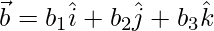 y
y 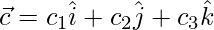 , entonces verifique que
, entonces verifique que 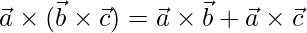 .
.
Solución:
Dado
,
y
=>
=>
=>
=>
…..eq(1)
Ahora,
=>
=>
Y,
=>
=>
De este modo,
=>
=>
…ecuación(2)
Así eq(1) = eq(2)
Por lo tanto probado.
Pregunta 34(i). Usando vectores encuentra el área del triángulo con los vértices A(1, 1, 2), B(2, 3, 5) y C(1, 5, 5).
Solución:
Dado, A(1, 1, 2), B(2, 3, 5) y C(1, 5, 5)
=>
=>
=>
Ahora 2 lados del triángulo están dados por,
=>
=>
=>
=>
=>
=>
=>
=>
El área del triángulo cuyos lados adyacentes se dan es
=>
=>
=>
Por lo tanto, el área del triángulo es,
=> Área =
=> Área =
=> Área = √61/2
Pregunta 34(ii). Usando vectores encuentra el área del triángulo con los vértices A(1, 2, 3), B(2, -1, 4) y C(4, 5, -1).
Solución:
Dado, A(1, 2, 3), B(2, -1, 4) y C(4, 5, -1)
=>
=>
=>
Ahora 2 lados del triángulo están dados por,
=>
=>
=>
=>
=>
=>
=>
=>
El área del triángulo cuyos lados adyacentes se dan es
=>
=>
=>
Por lo tanto, el área del triángulo es,
=> Área =
=> Área =
=> Área = √274/2
Pregunta 35. Encuentra todos los vectores de magnitud 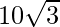 que son perpendiculares al plano de
que son perpendiculares al plano de 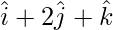 y
y 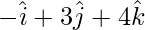 .
.
Solución:
dado,
y
Un vector perpendicular a ambos
y
es,
=>
=>
=>
vector unitario es,
=>
=>
=>
=>
Ahora los vectores de magnitud
están dados por,
=>
=> Vectores requeridos,
Pregunta 36. Los lados adyacentes de un paralelogramo son 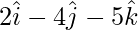 y
y 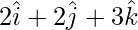 . Encuentra los 2 vectores unitarios paralelos a sus diagonales. Además, encuentre su área del paralelogramo.
. Encuentra los 2 vectores unitarios paralelos a sus diagonales. Además, encuentre su área del paralelogramo.
Solución:
dado,
y
=>
=>
=>
vector unitario es,
=>
=>
=>
El área está dada por
,
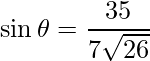
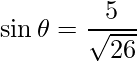
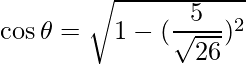
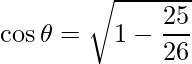
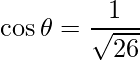
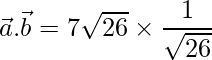
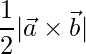
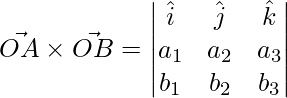
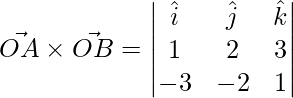
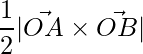
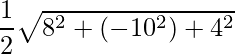
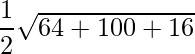
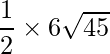
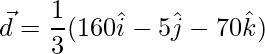
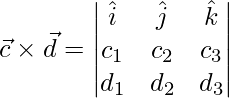
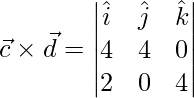
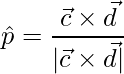
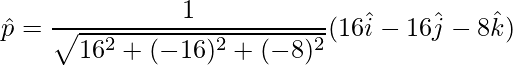
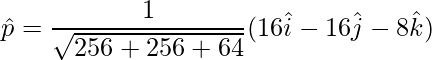
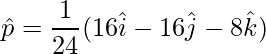
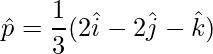
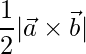
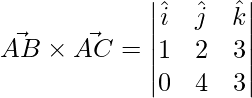
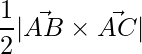
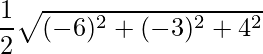
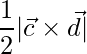
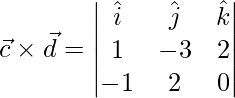
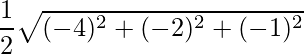
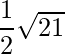
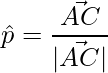
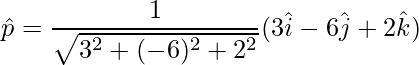
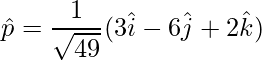
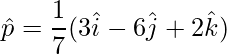
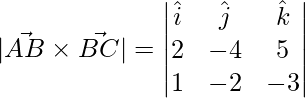
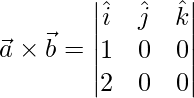
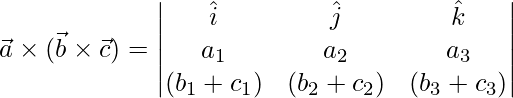
![Rendered by QuickLaTeX.com \vec{a}\times(\vec{b}\times\vec{c}) = \hat{i}[a_2(b_3+c_3)-a_3(b_2+c_2)]-\hat{j}[a_1(b_3+c_3)-a_3(b_1+c_1)]+\hat{k}[a_1(b_2+c_2)-a_2(b_1+c_1)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e6575ff3ed0bc464d72b6f539b305a0d_l3.png)
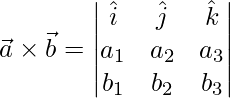
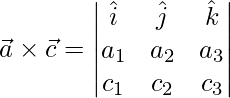
![Rendered by QuickLaTeX.com \vec{a}\times\vec{b}+\vec{a}\times\vec{c} = (\hat{i}[a_2b_3-b_2a_3]-\hat{j}[a_1b_3-b_1a_3]+\hat{k}[a_1b_2-b_1a_2]) + (\hat{i}[a_2b_3-c_2a_3]-\hat{j}[a_1c_3-c_1a_3]+\hat{k}[a_1c_2-c_1a_2])](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7994d23b8520437132356a4731507265_l3.png)