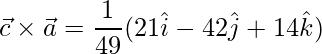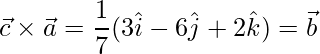Pregunta 1. Si 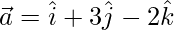 y
y 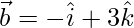 , encuentra
, encuentra 
Solución:
dado,
y
.
=>
=
=>
=
=>
=
=>
=
=>
=
Ahora,
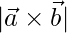
=>
=
=>
=
=>
= √91
Pregunta 2(i). Si 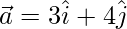 y
y 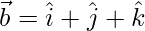 , encuentre el valor de
, encuentre el valor de 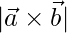
Solución:
dado,
y
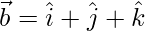
=>
=
=>
=
=>
=
=>
=
=>
=
Ahora,

=>
=
=>
=
=>
=
Pregunta 2(ii). Si 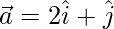 y
y 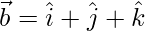 , encuentre la magnitud de
, encuentre la magnitud de 
Solución:
dado,
y
=>
=
=>
=
=>
=
=>
=
=>
=
Ahora,

=>
=
=>
=
=>
= √6
Pregunta 3(i). Encuentre un vector unitario perpendicular a ambos vectores 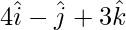 y
y 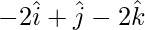
Solución:
Dado
y
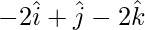
Un vector perpendicular a 2 vectores viene dado por

=>
=
=>
=
=>
=
=>
=
=>
=
El vector unitario viene dado por
=>
=
=>
=
=>
= 3
=> El vector unitario es,
=>
=
Pregunta 3(ii). Encuentre un vector unitario perpendicular al plano que contiene los vectores 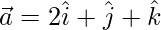 y
y  .
.
Solución:
dado,
y

Un vector perpendicular a 2 vectores viene dado por
=>
=
=>
=
=>
=
=>
=
=>
=
El vector unitario viene dado por
=>
=
=>
=
=>
=
=> El vector unitario es,
=>
=
Pregunta 4. Encuentra la magnitud del vector 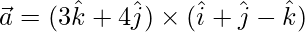
Solución:
Dado
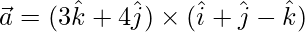
=>

=>
=
=>
=
=>
=
=>
=
vector unitario es,
=>
=
=>
=
=>
= √74
Pregunta 5. Si 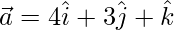 y
y  , entonces encuentra
, entonces encuentra 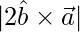
Solución:
dado,
y

=>
=
=>
=
=>
=
=>
=
=>
=
=>
=
=>
=
=>
=
Ahora,
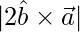
=>
=
=>
=
=>
=
Pregunta 6. Si 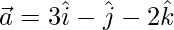 y
y 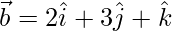 , encuentra
, encuentra 
Solución:
dado,
y
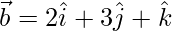
=>
=
=>
=
=>
=
=>
=
=>
=
=>
=
=>
=
=>
=
=>
=
=>
=
=>
=
=>
=
=>
=
=>
=
Pregunta 7(i). Encuentre un vector de magnitud 49, que sea perpendicular a ambos vectores 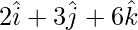 y
y 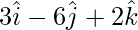
Solución:
dado,
y
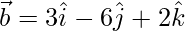
Un vector perpendicular a 2 vectores viene dado por
=>
=
=>
=
=>
=
=>
=
=>
=
La magnitud del vector está dada por,
=>
=
=>
=
=>
=
=>
=
=> Vector es,
Pregunta 7(ii). Encuentre el vector cuya longitud es 3 y que es perpendicular al vector 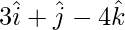 y
y 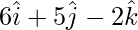
Solución:
dado,
y
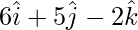
Un vector perpendicular a 2 vectores viene dado por
=>
=
=>
=
=>
=
=>
=
=>
=
La magnitud del vector está dada por,
=>
=
=>
=
=>
=
=>
= 27
=> El vector unitario es,
=>
=
=>
=
El vector requerido es,
=>
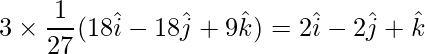
Pregunta 8(i). Encuentre el paralelogramo determinado por los vectores: 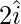 y
y 
Solución:
Dado eso,
y

=> El área del paralelogramo es
=>
=
=>
=
=>
=
=>
=
=>
=
Por tanto, el área del paralelogramo es,
=>
=
=>
=
=> Área = 6 unidades cuadradas.
Pregunta 8(ii). Encuentra el paralelogramo determinado por los vectores: 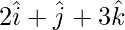 y
y 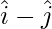 .
.
Solución:
Dado eso,
y
=> El área del paralelogramo es
=>
=
=>
=
=>
=
=>
=
=>
=
Por lo tanto, el área del paralelogramo es,
=>
=
=>
=
=> Área =
Pregunta 8(iii). Encuentre el área del paralelogramo determinada por los vectores: 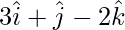 y
y 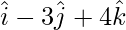
Solución:
Dado eso,
y
=> El área del paralelogramo es
=>
=
=>
=
=>
=
=>
=
=>
=
Por tanto, el área del paralelogramo es,
=>
=
=>
=
=> Área =
Pregunta 8(iv). Encuentre el área del paralelogramo determinada por los vectores: 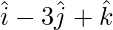 y
y 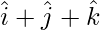
Solución:
Dado eso,
y
=> El área del paralelogramo es
=>
=
=>
=
=>
=
=>
=
=>
=
Por tanto, el área del paralelogramo es,
=>
=
=>
=
=> Área =
Pregunta 9(i). Encuentre el área del paralelogramo cuyas diagonales son: 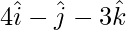 y
y 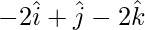
Solución:
dado,
y
=> El área del paralelogramo es
=>
=
=>
=
=>
=
=>
=
=>
=
Por tanto, el área del paralelogramo es,
=>
=
=>
=
=> Área = 15/2 = 7,5 unidades cuadradas
Pregunta 9(ii). Encuentre el área del paralelogramo cuyas diagonales son: 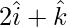 y
y 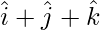
Solución:
dado,
y
=> El área del paralelogramo es
=>
=
=>
=
=>
=
=>
=
=>
=
Por tanto, el área del paralelogramo es,
=>
=
=>
=
=> Área =
Pregunta 9(iii). Encuentre el área del paralelogramo cuyas diagonales son: 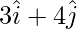 y
y 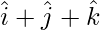
Solución:
dado,
y
=> El área del paralelogramo es
=>
=
=>
=
=>
=
=>
=
=>
=
Por tanto, el área del paralelogramo es,
=>
=
=>
=
=> Área =
Pregunta 9(iv). Encuentre el área del paralelogramo cuyas diagonales son: 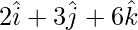 y
y 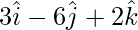
Solución:
dado,
y
=> El área del paralelogramo es
=>
=
=>
=
=>
=
=>
=
=>
=
Por tanto, el área del paralelogramo es,
=>
=
=>
=
=> Área =
=> Área = 24.5
Pregunta 10. Si 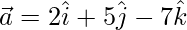 ,
, 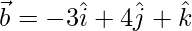 y
y 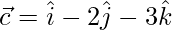 , calcule
, calcule 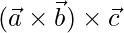 y
y 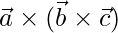 verifique que estos no son iguales.
verifique que estos no son iguales.
Solución:
dado
,
y
=>
=
=>
=
=>
=
=>
=
=>
=
=>
=
=>
=
=>
=
=>
=
=>
=
=>
=
=>
=
=>
=
=>
=
=>
=
=>
=
=>
no es igual a
=> Por lo tanto verificado.
Pregunta 11. Si 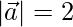 ,
, 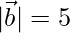 y
y 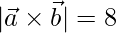 , encuentran
, encuentran 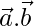
Solución:
Lo sabemos,
=>
=>
Sabemos que
es 1, ya que
es un vector unitario
=>
=>
=>
También,
=>
Y
=>
=>
=>
=>
=>
=>
Pregunta 12. Dado que 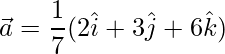 ,
, 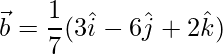 ,
, 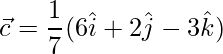 ,
, 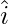 ,
, 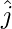 ,
, 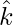 es un sistema ortogonal derecho de vectores unitarios en el espacio, demuestre que
es un sistema ortogonal derecho de vectores unitarios en el espacio, demuestre que  y
y  también
también 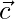 es otro sistema.
es otro sistema.
Solución:
Para demostrar que
,
y
es un sistema ortogonal de vectores unitarios de mano derecha, necesitamos probar:
(1)
=>
=>
=>
=>
=>
=>
=>
=>
=>
=>
=>
=>
=>
=>
=>
(2)
=>
=>
=>
=>
=>
(3)
=>
=>
=>
=>
=>
(4)
=>
=>
=>
=>
=>
Por lo tanto probado.
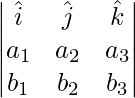
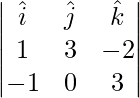

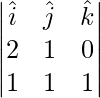
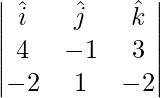
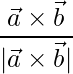
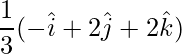


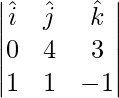
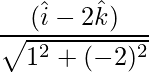
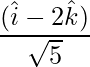
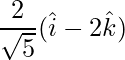
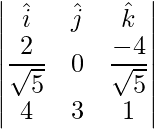
![Rendered by QuickLaTeX.com \hat{i}[(0)(1)-(3)(-\dfrac{4}{\sqrt{5}})]-\hat{j}[(\dfrac{2}{\sqrt{5}})(1)-(4)(\dfrac{-4}{\sqrt{5}})]+\hat{k}[(\dfrac{2}{\sqrt{5}})(3)-(4)(0)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-38548a3b218ebf987f09d572c0358b4b_l3.png)
![Rendered by QuickLaTeX.com \hat{i}[0+\dfrac{12}{\sqrt{5}}]-\hat{j}[\dfrac{2}{\sqrt{5}}+\dfrac{16}{\sqrt{5}}]+\hat{k}[\dfrac{6}{\sqrt{5}}-0]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9695d37e8407ccea9e8021650de1bb4b_l3.png)
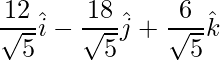
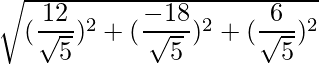
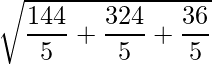
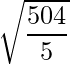
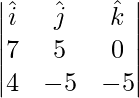
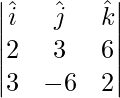
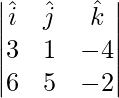



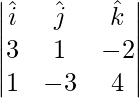
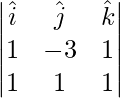
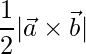


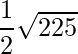
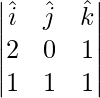
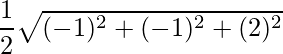
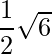
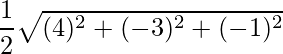
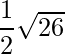
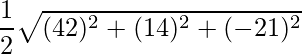
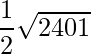
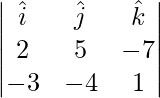
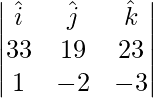

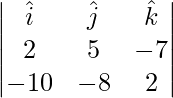
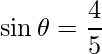
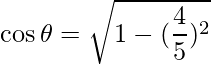

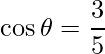
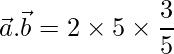
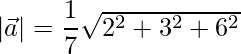
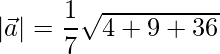

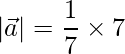
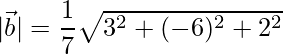

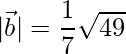
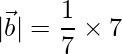
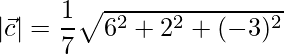
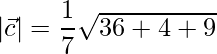
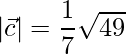
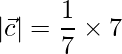
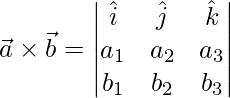
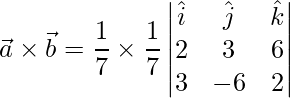
![Rendered by QuickLaTeX.com \vec{a}\times\vec{b} = \dfrac{1}{49}(\hat{i}[6+36]-\hat{j}[4-18]+\hat{k}[-12-9])](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f08b6375737c58d914b2d7f4f7313ba0_l3.png)
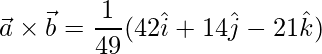
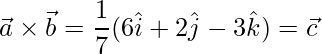
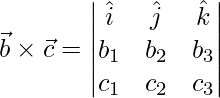
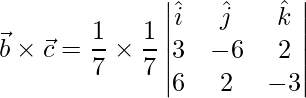
![Rendered by QuickLaTeX.com \vec{b}\times\vec{c} = \dfrac{1}{49}(\hat{i}[18-4]-\hat{j}[-9-12]+\hat{k}[6+36])](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-98b3ef0e492b4928a0a19ca34514e63b_l3.png)
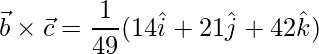

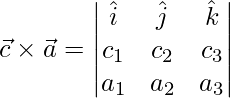
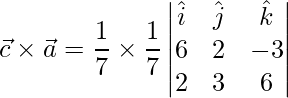
![Rendered by QuickLaTeX.com \vec{c}\times\vec{a} = \dfrac{1}{49}(\hat{i}[12+9]-\hat{j}[36+6]+\hat{k}[18-4])](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c168230ab608236f7647d8ce8b56d7ae_l3.png)