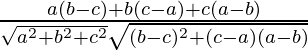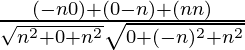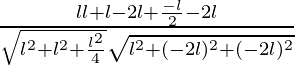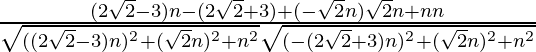Clase 12 Soluciones RD Sharma – Capítulo 27 Cosenos de dirección y razones de dirección – Ejercicio 27.1

Pregunta 1. Si una línea forma ángulos de 90°, 60° y 30° con la dirección positiva de los ejes x, y y z respectivamente. Encuentre sus cosenos directores.

Solución:

Consideremos los cosenos directores de la línea be l, m, n.

Como sabemos que los cosenos directores de una recta serán cosenos

del ángulo formado con los ejes x, y y z.

l = cos90° = 0

m = cos60° = 1/2

n = cos30° = √3/2

Por lo tanto, los cosenos directores de la línea son 0, 1/2, √3/2.

Pregunta 2. Si una línea tiene relaciones de dirección 2, -1, -2. Determine sus cosenos directores.

Solución:

Consideremos los cosenos directores de la línea be l, m, n.

Las relaciones de dirección dadas son 2, -1, -2.

Podemos determinar los cosenos directores l, m, n de una línea dada a partir de las razones de dirección r1, r2, r3 por

yo = $\frac{r1}{\sqrt{(r1)^2+(r2)^2+(r3)^2}}$

metro = $\frac{r2}{\sqrt{(r1)^2+(r2)^2+(r3)^2}}$

norte = $\frac{r3}{\sqrt{(r1)^2+(r2)^2+(r3)^2}}$

Aquí r1 = 2, r2 = -1, r3 = -2

De este modo,

l = $\frac{2}{\sqrt{2^2+(-1)^2+(-2)^2}}$ = 2/3

m = $\frac{-1}{\sqrt{2^2+(-1)^2+(-2)^2}}$ = -1/3

n = $\frac{-2}{\sqrt{2^2+(-1)^2+(-2)^2}}$ = -2/3

Por lo tanto, las relaciones de dirección de la línea dada son 2/3, -1/3, -2/3.

Pregunta 3. Encuentra los cosenos directores de la línea que pasa por dos puntos (-2, 4, -5) y (1, 2, 3).

Solución:

Consideremos que los cosenos directores de la recta que pasa por dos puntos A(x1, x2, x3) y B(y1, y2, y3) son

$\frac{x2-x1}{AB}$ , $\frac{y2-y1}{AB}$ , $\frac{z2-z1}{AB}$

Entonces, la distancia entre A y B = $\sqrt{(x2-x1)^2+(y2-y1)^2+(z2-z1)^2}$

Dado que A(-2, 4, -5), y B(1, 2, 3)

AB = $\sqrt{(1-(-2))^2+(2-4)^2+(3-(-5)^2)}$

= √77

Ahora, los cosenos directores serán $\frac{1-(-2)}{\sqrt77}$ , $\frac{2-(4)}{\sqrt77}$ , $\frac{3-(-5)}{\sqrt77}$

Por tanto, los cosenos directores de la recta que pasa por dos puntos A y B son $\frac3{\sqrt{77}}$ , $\frac{-2}{\sqrt{77}}$ , $\frac8{\sqrt{77}}$

Pregunta 4. Usando razones de dirección, muestra que los puntos A(2, 3, -4), B(1, -2, 3), C(3, 8, -11) son colineales.

Solución:

Los puntos dados son A(2, 3, -4), B(1, -2, 3), C(3, 8, -11)

Consideremos que las relaciones de dirección de la línea que une los puntos (x1, y1, z1) y (x2, y2, z2) son x2 – x1, y2 – y1, z2 – z1.

Entonces, las relaciones de dirección de la línea que une A y B son (1 – 2, -2 – 3, 3 – (-4)) es decir (-1, -5, 7)

Y las relaciones de dirección de la línea que une B y C son (3 – 1, 8 – (-2), -11 – 3) es decir (2, 10, -14)

Supongamos que las relaciones de dirección para AB sean (r1, r2, r3) y BC sean (r4, r5, r6)

Entonces, se dice que los puntos A, B y C son colineales cuando r1/r4 = r2/r5 = r3/r6 = constante

Aquí (r1, r2, r3) = (-1, -5, 7) y (r4, r5, r6) = (2, 10, -14)

Ahora,

r1/r4 = -1/2

r2/r5 = -5/10 = -1/2

r3/r6 = 7/-14 = -1/2

Aquí, $\frac{r1}{r4}=\frac{r2}{r5}=\frac{r3}{r6}=\frac{-1}2$

Por lo tanto, A(2, 3, -4), B(1, -2, 3) y C(3, 8, -11) son colineales.

Pregunta 5. Encuentra los cosenos directores de los lados de un triángulo cuyos vértices son (3, 5, -4), (-1, 1, 2), (-5, -5, -2).

Solución:

Consideremos que ABC es un triángulo cuyos vértices son A(3, 5, -4), B(-1, 1, 2), C(-5, -5, -2).

Entonces, las relaciones de dirección para AB son (-1 – 3, 1 – 5, 2 – (-4)) = (-4, -4, 6)

Cosenos directores para AB = $\frac{-4}{\sqrt{(-4)^2+(-4)^2+(6^2)}}$ , $\frac{-4}{\sqrt{(-4)^2+(-4)^2+(6^2)}}$ , $\frac{6}{\sqrt{(-4)^2+(-4)^2+(6^2)}}$

= $\frac{-4}{2\sqrt{17}}$ , $\frac{-4}{2\sqrt{17}}$ , $\frac{6}{2\sqrt{17}}$

= $\frac{-2}{\sqrt{17}}$ , $\frac{-2}{\sqrt{17}}$ , $\frac{3}{\sqrt{17}}$

Las relaciones de dirección para BC son (-5 – (-1), -5 – 1, -2 – 2) = (-4, -6, -4)

Cosenos directores para BC = $\frac{-4}{\sqrt{(-4)^2+(-6)^2+(-4)^2}}$ , $\frac{-6}{\sqrt{(-4)^2+(-6)^2+(-4)^2}}$ , $\frac{-4}{\sqrt{(-4)^2+(-6)^2+(-4)^2}}$

= $\frac{-4}{2\sqrt{17}}$ , $\frac{-6}{2\sqrt{17}}$ , $\frac{-4}{2\sqrt{17}}$

= $\frac{-2}{\sqrt{17}}$ , $\frac{-3}{\sqrt{17}}$ , $\frac{-2}{\sqrt{17}}$

Las relaciones de dirección para CA son (-5 – 3, -5 – 5, -2 – (-4)) ⇒ (-8, -10, 2)

Cosenos directores para CA = $\frac{-8}{\sqrt{(-8)^2+(-10)^2+(2)^2}}$ , $\frac{-10}{\sqrt{(-8)^2+(-10)^2+(2)^2}}$ , $\frac{2}{\sqrt{(-8)^2+(-10)^2+(2)^2}}$

= $\frac{-8}{2\sqrt{42}}$ , $\frac{-10}{2\sqrt{42}}$ , $\frac{2}{2\sqrt{42}}$

= $\frac{-4}{\sqrt{42}}$ , $\frac{-5}{\sqrt{42}}$ , $\frac{1}{\sqrt{42}}$

Pregunta 6. Encuentra el ángulo entre los vectores con relaciones de dirección proporcionales a 1, -2, 1 y 4, 3, 2.

Solución:

Sea $\vec{a}$ un vector con relaciones de dirección 1, -2, 1

$\vec{a}$ = $\hat{i}-2\hat{j}+\hat{k}$

Sea $\vec{b}$ un vector con relaciones de dirección 4, 3, 2.

$\vec{b}$ = $4\hat{i}+3\hat{j}+2\hat{k}$

Sean $\theta$ ángulos entre vectores

porque= $\frac{\vec{a}.\vec{b}}{|\vec{a}||\vec{b}|}$

= $\frac{(\hat{i}-2\hat{j}+\hat{k})(4\hat{i}+3\hat{j}+2\hat{k})}{|\hat{i}-2\hat{j}+\hat{k}||4\hat{i}+3\hat{j}+2\hat{k}|}$

= $\frac{4-6+2}{\sqrt{1+4+1}{\sqrt{16+9+4}}}$

= 0

cos= 0 ⇒

Por lo tanto, el ángulo entre los vectores dados son

Pregunta 7. Encuentra el ángulo entre los vectores con cosenos directores proporcionales a 2, 3, -6 y 3, -4, 5.

Solución:

Sea $\vec{a}$ un vector con relaciones de dirección 2, 3, -6

⇒ $\vec{a}=2\hat{i}+3\hat{j}-6\hat{k}$

Sea $\vec{b}$ un vector con relaciones de dirección 3, -4, 5

⇒ $\vec{b}=3\hat{i}-4\hat{j}+5\hat{k}$

Sean $\theta$ ángulos entre vectores

porque= $\frac{\vec{a}.\vec{b}}{|\vec{a}||\vec{b}|}$

= $\frac{(2\hat{i}+3\hat{j}-6\hat{k}).(3\hat{i}-4\hat{j}+5\hat{k})}{|2\hat{i}+3\hat{j}-6\hat{k}||3\hat{i}-4\hat{j}+5\hat{k}|}$

= $\frac{6-12-30}{\sqrt{4+9+36}\sqrt{9+16+25}}$

= $\frac{-36}{\sqrt{49}\sqrt{50}}$

= $\frac{-36}{35\sqrt2}$

= $\frac{-36×\sqrt2}{35×\sqrt2×\sqrt2}$

= $\frac{-18\sqrt2}{35}$

= $cos^{-1}(\frac{-18\sqrt2}{35})$

Por lo tanto, el ángulo entre los vectores dados es $cos^{-1}(\frac{-18\sqrt2}{35})$

Pregunta 8. Encuentra el ángulo agudo entre las líneas cuyas relaciones de dirección son proporcionales a 2:3:6 y 1:2:2.

Solución:

Sea $\vec{a}$ un vector con relaciones de dirección 2, 3, 6

⇒ $\vec{a}=2\hat{i}+3\hat{j}+6\hat{k}$

Sea $\vec{b}$ un vector con relaciones de dirección 1, 2, 2

⇒ $\vec{b}=\hat{i}+2\hat{j}+2\hat{k}$

Sean ángulos entre vectores

porque = $\frac{\vec{a}.\vec{b}}{|\vec{a}||\vec{b}|}$

= $\frac{(2\hat{i}+3\hat{j}+6\hat{k}).(\hat{i}+2\hat{j}+2\hat{k})}{|2\hat{i}+3\hat{j}+6\hat{k}||\hat{i}+2\hat{j}+2\hat{k}|}$

= $\frac{2+6+12}{\sqrt{4+9+36}\sqrt{1+4+4}}$

= $\frac{20}{21}$

= $cos^{-1}(\frac{20}{21})$

Por lo tanto, el ángulo entre los vectores dados es $cos^{-1}(\frac{20}{21})$

Pregunta 9. Demuestra que los puntos (2, 3, 4), (-1, -2, 1), (5, 8, 7) son colineales.

Solución:

Se da que A(2, 3, 4), B(-1, -2, 1) y C(5, 8, 7) son colineales,

por lo tanto, las relaciones de dirección de dos líneas cualquiera de AB, BC, CA deben ser proporcionales.

Supongamos que las relaciones de dirección para AB son (r1, r2, r3) y BC son (r4, r5, r6)

La constante de proporcionalidad se puede establecer como r1/r4 = r2/r5 = r3/r6 = constante

Relaciones de dirección para AB = (-1 – 2, -2 – 3, 1 – 4) = (-3, -5, -3)

⇒ r1 = -3, r2 = -5, r3 = -3

Relaciones de dirección para BC = (5 – (-1), 8 – (-2), 7 – 1) = (6, 10, 6)

⇒ r4 = 6, r5 = 10, r6 = 6

r1/r4 = -3/6 = -1/2

r2/r5 = -5/10 = -1/2

r3/r6 = -3/6 = -1/2

Asi que, $\frac{r1}{r4}=\frac{r2}{r5}=\frac{r3}{r6}=\frac{-1}2$

Por lo tanto, los puntos dados son colineales.

Pregunta 10. Demuestra que la recta que pasa por los puntos (4, 7, 8) y (2, 3, 4) es paralela a la recta que pasa por los puntos (-1, -2, 1) y (1, 2, 5) .

Solución:

Los puntos dados son A(4, 7, 8), B(2, 3, 4), C(-1, -2, 1) y D(1, 2, 5)

Además, se dice que las dos líneas son paralelas si las relaciones de dirección de las dos líneas son proporcionales.

Ahora, supongamos que las relaciones de dirección para AB son (r1, r2, r3) y CD es (r4, r5, r6)

Relación de dirección para AB = (2 – 4, 3 – 7, 4 – 8)

⇒ (r1, r2, r3) = (-2,-4,-4)

⇒ r1 = -2, r2 = -4, r3 = -4

Relación de dirección para CD = (1 – (-1), 2 – (-2), 5 – 1)

⇒ (r4, r5, r6) = (2, 4, 4)

⇒ r4 = 2, r5 = 4, r6 = 4

La constante de proporcionalidad se puede establecer como r1/r4 = r2/r5 = r3/r6 = constante

r1/r4 = -2/2 = -1

r2/r5 = -4/4 = -1

r3/r6 = -4/4 = -1

Asi que, $\frac{r1}{r4}=\frac{r2}{r5}=\frac{r3}{r6}=-1$

Por tanto, la recta que pasa por los puntos (4, 7, 8) y (2, 3, 4) es paralela a

línea a través de los puntos (-1, -2, 1) y (1, 2, 5).

Pregunta 11. Demuestra que la recta que pasa por los puntos (1, -1, 2) y (3, 4, -2) es perpendicular a la recta que pasa por los puntos (0, 3, 2) y (3, 5, 6) .

Solución:

Los puntos dados son A(1, -1, 2), B(3, 4, -2), C(0, 3, 2) y D(3, 5, 6)

Como sabemos que las dos rectas con relaciones de dirección (r1, r2, r3) y (r4, r5, r6) son

perpendiculares entre sí si cumple la condición dada r1.r4 + r2.r5 + r3.r6 = 0

Supongamos que las relaciones de dirección para AB son (r1, r2, r3) y CD son (r4, r5, r6)

Relación de dirección para AB = (3 – 1, 4 – (-1), -2 – 2)

⇒ (r1, r2, r3) = (2, 5, -4)

⇒ r1 = 2, r2 = 5, r3 = -4

Relación de dirección para CD = (3 – 0, 5 – 3, 6 – 2)

⇒ (r4, r5, r6) = (3, 2, 4)

⇒ r4 = 3, r5 = 2, r6 = 4

Comprobemos el estado

r1.r4 + r2.r5 + r3.r6 = 2 × 3 + 5 × 2 + -4 × 4

= 6 + 10 – 16

= 0

Aquí, la condición se cumple, por lo que AB y CD son perpendiculares entre sí.

Por tanto, la recta que pasa por los puntos (1, -1, 2) y (3, 4, -2) es perpendicular

a la recta que pasa por los puntos (0, 3, 2) y (3, 5, 6).

Pregunta 12. Demuestra que la recta que une el origen con el punto (2, 1, 1) es perpendicular a la recta determinada por los puntos (3, 5, -1) y (4, 3, -1).

Solución:

Los puntos dados son O(0, 0, 0), A(2, 1, 1), B(3, 5, -1) y C(4, 3, -1)

Como sabemos que las dos rectas con relaciones de dirección (r1, r2, r3) y (r4, r5, r6) son

perpendiculares entre sí si cumple la condición dada r1.r4 + r2.r5 + r3.r6 = 0

Supongamos que las relaciones de dirección para OA son (r1, r2, r3) y BC son (r4, r5, r6)

Relaciones de dirección para OA = (2 – 0, 1 – 0, 1 – 0)

⇒ (r1, r2, r3) = (2, 1, 1)

⇒ r1 = 2, r2 = 1, r3 = 1

Relaciones de dirección para BC = (4 – 3, 3 – 5, -1 – (-1))

⇒ (r4, r5, r6) = (1, -2, 0)

⇒ r4 = 1, r5 = -2, r6 = 0

Ahora comprueba la condición

r1.r4 + r2.r5 + r3.r6 = 2 × 1 + 1 × -2 + 1 × 0

= 2 – 2

= 0

Aquí, la condición se cumple, por lo que OA y BC son perpendiculares entre sí.

Por tanto, la recta que une el origen con el punto (2, 1, 1) es perpendicular a

línea determinada por los puntos (3, 5, -1) y (4, 3, -1).

Pregunta 13. Encuentra el ángulo entre las líneas cuyas relaciones de dirección son proporcionales a a, b, c y b – c, c – a, a – b.

Solución:

Supongamos a1 = a, b1 = b, c1 = c

y a2 = b – c, b2 = c – a, c2 = a – b

Sean los ángulos entre las rectas dadas

porque = $\frac{a1a2+b1b2+c1c2}{\sqrt{(a1)^2+(b1)^2+(c1)^2}\sqrt{(a2)^2+(b2)^2+(c2)^2}}$

= $\frac{a(b-c)+b(c-a)+c(a-b)}{\sqrt{a^2+b^2+c^2}\sqrt{(b-c)^2+(c-a)(a-b)}}$

= $\frac{ab-ac+bc-ab+ac-bc}{\sqrt{a^2+b^2+c^2}\sqrt{(b-c)^2+(c-a)(a-b)}}$

= 0

⇒ =

Por lo tanto, el ángulo entre las líneas dadas es de 90°.

Pregunta 14. Si las coordenadas de los puntos A, B, C, D son (1, 2, 3), (4, 5, 7), (-4, 3, -6) y (2, 9, 2 ). Luego encuentra el ángulo entre AB y CD.

Solución:

Los puntos dados son A(1, 2, 3), B(4, 5, 7), C(-4, 3, -6) y D(2, 9, 2)

Supongamos que las relaciones de dirección para AB son (r1, r2, r3) y CD son (r4, r5, r6)

Relaciones de dirección para AB = (4 – 1, 5 – 2, 7 – 3)

⇒ (r1, r2, r3) = (3, 3, 4)

⇒ r1 = 3, r2 = 3, r3 = 4

Relaciones de dirección para CD = (2 – (-4), 9 – 3, 2 – (-6))

⇒ (r4, r5, r6) = (6, 6, 8)

⇒ r4 = 6, r5 = 6, r6 = 8

porque= $\frac{r1r4+r2r5+r3r6}{\sqrt{(r1)^2+(r2)^2+(r3)^2}\sqrt{(r4)^2+(r5)^2+(r6)^2}}$

= $\frac{18+18+32}{\sqrt{9+9+16}\sqrt{36+36+64}}$

= $\frac{68}{68}$

= 1

⇒ = 0°

Por lo tanto, el ángulo entre las líneas AB y CD es 0°.

Pregunta 15. Encuentra los cosenos directores de las líneas conectadas por relaciones: l + m + n = 0 y 2lm + 2ln – mn = 0.

Solución:

Dado que,

l + m + n = 0 ……..(1)

2lm + 2ln – mn = 0 ……..(2)

De la ecuación (1), obtenemos

l = -m – n

Al sustituir el valor de la ecuación (2), obtenemos

⇒ 2(-m – n)m + 2(-m – n)n – mn = 0

⇒ 2(-m ² – mn) + 2(-mn – n ² ) – mn = 0

⇒ -2m ² – 2mn – 2mn – 2n ² – mn = 0

⇒ -2m ² – 2n ² = 5mn

⇒ 2m ² + 2n ² + 5mn = 0

⇒ (m + 2n)(2m + n) = 0

⇒ m = -2n o m = -n/2

Si m = -2n, entonces l = n de eq(1)

Si m = -n/2, entonces l = -n/2 de eq(1)

Entonces, las relaciones de dirección de dos líneas proporcionales a (n, -2n, n) y (-n/2, -n/2, n), es decir, (1, -2, 1) y (-1/2, -1 /2, 1)

Ahora sus cosenos directores serán $\pm\frac1{\sqrt6},\pm\frac{-2}{\sqrt6},\pm\frac1{\sqrt6}$ y $\pm\frac{-1}{\sqrt6},\pm\frac{-1}{\sqrt6},\pm\frac2{\sqrt6}$

Pregunta 16(i). Encuentra el ángulo entre las líneas cuyos cosenos directores están dados por las ecuaciones l + m + n = 0 y l ² + m ² – n ² = 0.

Solución:

Dado que,

l + m + n = 0 ……..(1)

l ² + m ² – n ² = 0 ……..(2)

De la ecuación (1), obtenemos

l = -m – n

Al sustituir el valor de l en la ecuación (2), obtenemos

⇒ (-m – n) ² + m ² – n ² = 0

⇒ m ² + n ² + 2 min + m ² – n ² = 0

⇒ 2m ² + 2mn = 0

⇒ 2m(m + n) = 0

⇒ m = 0 o m = -n

Si m = 0 entonces l = -n de eq(1)

Si m = -n entonces l = 0 de eq(2)

Entonces, las relaciones de dirección para la primera línea son (-n, 0, n)

Las relaciones de dirección para la segunda línea son (0, -n, n)

Sean $\theta$ ángulos entre dos rectas

porque= $\frac{a1a2+b1b2+c1c2}{\sqrt{(a1)^2+(b1)^2+(c1)^2}\sqrt{(a2)^2+(b2)^2+(c2)^2}}$

Donde a1, b1, c1 son las relaciones de dirección de primera línea y

a2, b2, c2 son las relaciones de dirección de la segunda línea

= $\frac{(-n×0)+(0×-n)+(n×n)}{\sqrt{n^2+0+n^2}\sqrt{0+(-n)^2+n^2}}$

= $\frac{n^2}{\sqrt{2n^2}\sqrt{2n^2}}$

= 1/2

⇒ = $cos^{-1}(\frac12)$

= 60°

Por lo tanto, el ángulo entre dos rectas dadas es de 60°.

Pregunta 16(ii). Encuentre el ángulo entre las líneas cuyos cosenos directores están dados por las ecuaciones 2l – m + 2n = 0 y mn + nl + lm = 0.

Solución:

Dado que,

2l – m + 2n = 0 ……..(1)

mn + nl + lm = 0 ……..(2)

De la ecuación (1), obtenemos

m = 2l + 2n

Al sustituir el valor de m en la ecuación (2), obtenemos

⇒ (2l + 2n)n + nl + l(2l + 2n) = 0

⇒ 2ln + 2n ² + nl + 2l ² + 2ln = 0

⇒ 2n ² + 5ln + 2l ² = 0

⇒ (2n + l)(n + 2l) = 0

⇒ n = -l/2 o n = -2l

Si n = -l/2, entonces m = l

Si n = -2l, entonces m = -2l

Entonces, las proporciones de dirección para la primera línea son (l, l, -l/2)

Las relaciones de dirección para la segunda línea son (l, -2l, -2l)

Sean ángulos entre dos rectas

porque= $\frac{a1a2+b1b2+c1c2}{\sqrt{(a1)^2+(b1)^2+(c1)^2}\sqrt{(a2)^2+(b2)^2+(c2)^2}}$

Donde a1, b1, c1 son las relaciones de dirección de primera línea y

a2, b2, c2 son las relaciones de dirección de la segunda línea

= $\frac{l×l+l×-2l+\frac{-l}2×-2l}{\sqrt{l^2+l^2+\frac{l^2}4}\sqrt{l^2+(-2l)^2+(-2l)^2}}$

= 0°

⇒ = 90°

Por lo tanto, el ángulo entre dos rectas dadas es de 90°.

Pregunta 16(iii). Encuentra el ángulo entre las líneas cuyos cosenos directores están dados por las ecuaciones l + 2m + 3n = 0 y 3lm – 4ln + mn = 0.

Solución:

Dado que, l + 2m + 3n = 0 ……..(1)

3lm – 4ln + mn = 0 ……..(2)

De la ecuación (1), obtenemos

l = -2m – 3n

Al sustituir el valor de l en la ecuación (2), obtenemos

⇒ 3(-2m – 3n)m – 4(-2m – 3n)n + mn = 0

⇒ -6m ² – 9mn + 8mn + 12n ² + mn = 0

⇒ -6m ² + 12n ² = 0

⇒ 2n ² – m ² = 0

⇒ (√2n + m)(√2n – m) = 0

⇒ m = -√2n o m = √2n

Si m = -√2n entonces l = (2√2 – 3)n

Si m = √2n entonces l = -(2√2 + 3)n

Entonces, las relaciones de dirección para la primera línea son ((2√2 – 3)n, -√2n, n)

Las relaciones de dirección para la segunda línea son (-(2√2 + 3)n, √2n, n)

Sean ángulos entre dos rectas

porque= $\frac{a1a2+b1b2+c1c2}{\sqrt{(a1)^2+(b1)^2+(c1)^2}\sqrt{(a2)^2+(b2)^2+(c2)^2}}$

Donde a1, b1, c1 son las relaciones de dirección de primera línea y

a2, b2, c2 son las relaciones de dirección de la segunda línea.

= $\frac{(2\sqrt2-3)n×-(2\sqrt2+3)+(-\sqrt{2}n)×\sqrt{2}n+n×n}{\sqrt{((2\sqrt2-3)n)^2+(\sqrt2n)^2+n^2}\sqrt{(-(2\sqrt2+3)n)^2+(\sqrt2n)^2+n^2}}$

= 0

⇒ = 90°

Por lo tanto, el ángulo entre dos rectas dadas es de 90°.

Pregunta 16(iv). Encuentra el ángulo entre las líneas cuyos cosenos directores están dados por las ecuaciones 2l + 2m – n = 0 y mn + ln + lm = 0.

Solución:

Dado que,

2l + 2m – n = 0 ……..(1)

mn + ln + lm = 0 ……..(2)

De la ecuación (1), obtenemos

n = 2l + 2m

Al sustituir el valor de l en la ecuación (2), obtenemos

⇒ m(2l + 2m) + l(2l + 2m) + lm = 0

⇒ 2lm + 2m2 ⁺ 2l2 + 2lm ⁺ lm = 0

⇒ 2m2 ⁺ 5lm + 2l2 = ⁰

⇒ (2m + l)(m + 2l) = 0

⇒ m = -l/2 o m = -2l

Si m = -l/2 entonces n = l

Si m = -2l entonces n = -2l

Entonces, las proporciones de dirección para la primera línea son (l, -l/2, l)

Las relaciones de dirección para la segunda línea son (l, -2l, -2l)

Sean ángulos entre dos rectas

porque= $\frac{a1a2+b1b2+c1c2}{\sqrt{(a1)^2+(b1)^2+(c1)^2}\sqrt{(a2)^2+(b2)^2+(c2)^2}}$

Donde a1, b1, c1 son las relaciones de dirección de primera línea y

a2, b2, c2 son las relaciones de dirección de la segunda línea.

= $\frac{(l×l)+(-l/2×-2l)+(l×-2l)}{\sqrt{l^2+(-l/2)^2+l^2}\sqrt{l^2+(-2l)^2+(-2l)^2}}$

= $\frac{2l^2-2l^2}{\sqrt{l^2+(-l/2)^2+l^2}\sqrt{l^2+(-2l)^2+(-2l)^2}}$

= 0

⇒ = 90°

Por lo tanto, el ángulo entre dos rectas dadas es de 90°.

Publicación traducida automáticamente

Artículo escrito por prasanthinidamarthy y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Si una línea forma ángulos de 90°, 60° y 30° con la dirección positiva de los ejes x, y y z respectivamente. Encuentre sus cosenos directores.

Pregunta 2. Si una línea tiene relaciones de dirección 2, -1, -2. Determine sus cosenos directores.

Pregunta 3. Encuentra los cosenos directores de la línea que pasa por dos puntos (-2, 4, -5) y (1, 2, 3).

Pregunta 4. Usando razones de dirección, muestra que los puntos A(2, 3, -4), B(1, -2, 3), C(3, 8, -11) son colineales.

Pregunta 5. Encuentra los cosenos directores de los lados de un triángulo cuyos vértices son (3, 5, -4), (-1, 1, 2), (-5, -5, -2).

Pregunta 6. Encuentra el ángulo entre los vectores con relaciones de dirección proporcionales a 1, -2, 1 y 4, 3, 2.

Pregunta 7. Encuentra el ángulo entre los vectores con cosenos directores proporcionales a 2, 3, -6 y 3, -4, 5.

Pregunta 8. Encuentra el ángulo agudo entre las líneas cuyas relaciones de dirección son proporcionales a 2:3:6 y 1:2:2.

Pregunta 9. Demuestra que los puntos (2, 3, 4), (-1, -2, 1), (5, 8, 7) son colineales.

Pregunta 10. Demuestra que la recta que pasa por los puntos (4, 7, 8) y (2, 3, 4) es paralela a la recta que pasa por los puntos (-1, -2, 1) y (1, 2, 5) .

Pregunta 11. Demuestra que la recta que pasa por los puntos (1, -1, 2) y (3, 4, -2) es perpendicular a la recta que pasa por los puntos (0, 3, 2) y (3, 5, 6) .

Pregunta 12. Demuestra que la recta que une el origen con el punto (2, 1, 1) es perpendicular a la recta determinada por los puntos (3, 5, -1) y (4, 3, -1).

Pregunta 13. Encuentra el ángulo entre las líneas cuyas relaciones de dirección son proporcionales a a, b, c y b – c, c – a, a – b.

Pregunta 14. Si las coordenadas de los puntos A, B, C, D son (1, 2, 3), (4, 5, 7), (-4, 3, -6) y (2, 9, 2 ). Luego encuentra el ángulo entre AB y CD.

Pregunta 15. Encuentra los cosenos directores de las líneas conectadas por relaciones: l + m + n = 0 y 2lm + 2ln – mn = 0.

Pregunta 16(i). Encuentra el ángulo entre las líneas cuyos cosenos directores están dados por las ecuaciones l + m + n = 0 y l 2 + m 2 – n 2 = 0.

Pregunta 16(ii). Encuentre el ángulo entre las líneas cuyos cosenos directores están dados por las ecuaciones 2l – m + 2n = 0 y mn + nl + lm = 0.

Pregunta 16(iii). Encuentra el ángulo entre las líneas cuyos cosenos directores están dados por las ecuaciones l + 2m + 3n = 0 y 3lm – 4ln + mn = 0.

Pregunta 16(iv). Encuentra el ángulo entre las líneas cuyos cosenos directores están dados por las ecuaciones 2l + 2m – n = 0 y mn + ln + lm = 0.

Deja una respuesta Cancelar la respuesta

Pregunta 16(i). Encuentra el ángulo entre las líneas cuyos cosenos directores están dados por las ecuaciones l + m + n = 0 y l ² + m ² – n ² = 0.