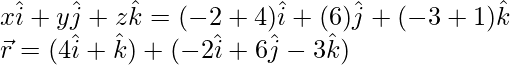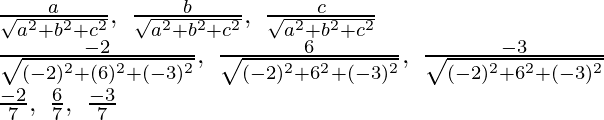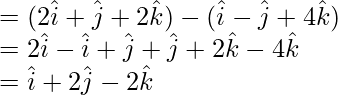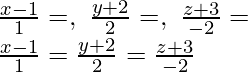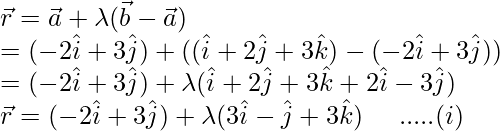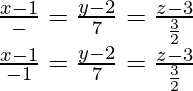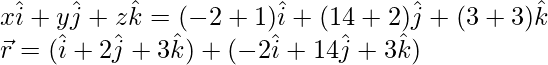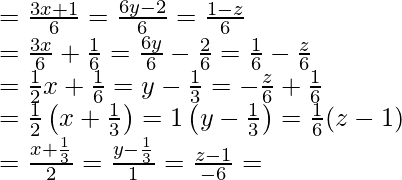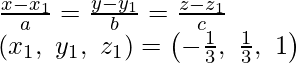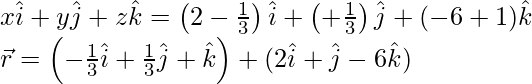Clase 12 Soluciones RD Sharma – Capítulo 28 La línea recta en el espacio – Ejercicio 28.1

Pregunta 11. Encuentra los cosenos directores de la recta 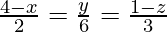$\frac{4-x}{2}=\frac{y}{6}=\frac{1-z}{3}$ . Además, redúcelo a forma vectorial.

Solución:

Dado:

$\frac{4-x}{2}=\frac{y}{6}=\frac{1-z}{3}$

$\frac{x-4}{-2}=\frac{y}{6}=\frac{1-z}{-3}=\lambda$

x = -2λ + 4, y = 6λ, z = -3λ + 1

Asi que,

$x\hat{i}+y\hat{j}+z\hat{k}=(-2λ+4)\hat{i}+(6λ)\hat{j}+(-3λ+1)\hat{k}\\ \vec{r}=(4\hat{i}+\hat{k})+λ(-2\hat{i}+6\hat{j}-3\hat{k})$

Las relaciones de dirección de la línea son = -2, 6, -3

Los cosenos directores de las rectas son,

$\frac{a}{\sqrt{a^2+b^2+c^2}},\ \frac{b}{\sqrt{a^2+b^2+c^2}},\ \frac{c}{\sqrt{a^2+b^2+c^2}}\\ \frac{-2}{\sqrt{(-2)^2+(6)^2+(-3)^2}},\ \frac{6}{\sqrt{(-2)^2+6^2+(-3)^2}},\ \frac{-3}{\sqrt{(-2)^2+6^2+(-3)^2}}\\ \frac{-2}{7},\ \frac{6}{7},\ \frac{-3}{7}$

Pregunta 12. Las ecuaciones cartesianas de una recta son x = ay + b, z = cy + d. Encuentre sus razones de dirección y redúzcalo a forma vectorial.

Solución:

x = ay + b

z = cy + d

$\frac{x-b}{a}=\frac{y}{1}=\frac{z-d}{c}=\lambda$

Entonces, los DR de la línea son (a, 1, c)

De la ecuación anterior, podemos escribir

x = aλ + b

y = l

z = cλ + d

Entonces la ecuación vectorial de la recta es

$x\hat{i}+y\hat{j}+z\hat{k}=(b\hat{i}+d\hat{k})+λ(a\hat{i}+\hat{j}+c\hat{k})$

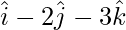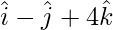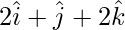Pregunta 13. Hallar la ecuación vectorial de una recta que pasa por el punto con vector de posición $\hat{i}-2\hat{j}-3\hat{k}$ y paralela a la recta que une los puntos con vector de posición $\hat{i}-\hat{j}+4\hat{k}$ y $2\hat{i}+\hat{j}+2\hat{k}$ . Además, encuentre el equivalente cartesiano de esta ecuación.

Solución:

Sabemos que, la ecuación de una recta que pasa por $\vec{a}$ y paralela al vector $\vec{b}$ es

$\vec{r}=\vec{a}+λ\vec{b}$ ……. (i)

Aquí,

$\vec{a}=\hat{i}-2\hat{j}-3\hat{k}$

y, \vec{b} = línea que une $(\hat{i}-\hat{j}+4\hat{k})$ y $(2\hat{i}+\hat{j}+2\hat{k})$

$=(2\hat{i}+\hat{j}+2\hat{k})-(\hat{i}-\hat{j}+4\hat{k})\\ =2\hat{i}-\hat{i}+\hat{j}+\hat{j}+2\hat{k}-4\hat{k}\\ =\hat{i}+2\hat{j}-2\hat{k}$

La ecuación de la recta es

$\vec{r}=(\hat{i}-2\hat{j}-3\hat{k})+\lambda(\hat{i}+2\hat{j}-2\hat{k})$

Para la forma cartesiana de ecuación poner $x\hat{i}+y\hat{j}+z\hat{k}$

$x\hat{i}+y\hat{j}+z\hat{k}=(1+\lambda)+\hat{i}(-2+2\lambda)\hat{j}+(-3-2\lambda)\hat{k}$

Igualando los coeficientes de $\hat{i},\ \hat{j},\ \hat{k}$

x = 1 + λ, y = -2 + 2λ, z = -3 – 2λ

$\frac{x-1}{1}=λ,\ \frac{y+2}{2}=λ,\ \frac{z+3}{-2}=λ\\ \frac{x-1}{1}=\frac{y+2}{2}=\frac{z+3}{-2}$

Pregunta 14. Encuentra los puntos en la recta 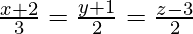$\frac{x+2}{3}=\frac{y+1}{2}=\frac{z-3}{2}$ a una distancia de 5 unidades de los puntos P(1, 3, 3).

Solución:

Dado, la línea es $\frac{x+2}{3}=\frac{y+1}{2}=\frac{z-3}{2}=\lambda$

Puntos generales Q en línea es (3λ – 2, 2λ -1), 2λ + 3)

Distancia de los puntos P a Q = $\sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}$

PQ = $\sqrt{(3λ-2-1)^2+(2λ-1-3)^2+(2λ+3-3)^2}$

(5) ² = (3λ -3) ² + (2λ – 4) + (2λ) ²

25 = 9λ ² + 9 – 18λ + 4λ ² + 16 – 16λ + 4λ ²

17λ ² – 34λ = 0

17λ (λ – 2) = 0

λ = 0 o 2

Entonces, los puntos en la recta son (3(0) – 2, 2(0) – 1, 2(0) + 3)

(3(2) – 2, 2(2) – 1, 2(2) + 3)

= (-2, -1, 3), (4, 3, 7)

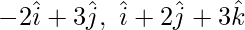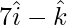Pregunta 15. Demostrar que los puntos cuyos vectores de posición son $-2\hat{i}+3\hat{j},\ \hat{i} + 2\hat{j}+3\hat{k}$ y $7\hat{i}-\hat{k}$ son colineales.

Solución:

Sean los puntos dados A,BC con vectores de posición $\vec{a},\ \vec{b},\ \vec{c}$ respectivamente.

$\vec{a}=2\hat{i}+3\hat{j},\ \vec{b}=\hat{i}+2\hat{j}+3\hat{k},\ \vec{c}=7\hat{i}-\hat{k}$

Sabemos que, ecuación de una recta que pasa por $\vec{a}$ y $\vec{b}$ son

$\vec{r}=\vec{a}+\lambda(\vec{b}-\vec{a})\\ =(-2\hat{i}+3\hat{j})+λ((\hat{i}+2\hat{j}+3\hat{k})-(-2\hat{i}+3\hat{j}))\\ =(-2\hat{i}+3\hat{j})+\lambda(\hat{i}+2\hat{j}+3\hat{k}+2\hat{i}-3\hat{j})\\ \vec{r}=(-2\hat{i}+3\hat{j})+\lambda(3\hat{i}-\hat{j}+3\hat{k})\ \ \ \ .....(i)$

Si A, B, C son colineales, entonces $\vec{c}$ deben satisfacer la ecuación (i)

$7\hat{i}-\hat{k}=(-2+3\lambda)\hat{i}+(3-\lambda)\hat{j}+(3\lambda)\hat{k}$

Ecuacionar los coeficientes de $\vec{i},\ \vec{j},\ \vec{k}$

-2 + 3 = 7 , λ = 3

3 – λ = 0 , λ = 3

3λ = -1, λ = $-\frac{1}{3}$

Como los valores de λ no son iguales, entonces,

Los puntos dados son colineales.

Pregunta 16. Encuentra las ecuaciones cartesianas y vectoriales de una recta que pasa por los puntos (1, 2, 3) y es paralela a la recta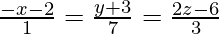 $\frac{-x-2}{1}=\frac{y+3}{7}=\frac{2z-6}{3}$

Solución:

Sabemos que, la ecuación de una línea que pasa por un punto (x ₁ , y ₁ , z ₁ ) y que tiene relaciones de dirección proporcionales a a, b, c es

$\frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{c}\ \ \ \ .....(i)$

Aquí,

(x ₁ , y ₁ , z ₁ ) = (1, 2, 3) y

línea dada $\frac{-x-2}{1}=\frac{y+3}{7}=\frac{2z-6}{3}$

$\frac{x+2}{-1}=\frac{y+3}{7}=\frac{z-3}{\frac{3}{2}}$

Es paralelo a la línea requerida, por lo que

a = μ , b = 7 μ , c = $\frac{3}{2}$ μ

Entonces, la ecuación de la línea requerida usando la ecuación (i) es,

$\frac{x-1}{-μ }=\frac{y-2}{7μ }=\frac{z-3}{\frac{3}{2}μ }\\ \frac{x-1}{-1}=\frac{y-2}{7}=\frac{z-3}{\frac{3}{2}}$

Multiplicando los denominadores por 2

$\frac{x-1}{-2}=\frac{y-2}{14}=\frac{z-3}{3}=λ$

x = -2λ + 1, y = 14λ + 2, z = 3λ + 3

Entonces, forma vectorial de la ecuación de la línea requerida,

$x\hat{i}+y\hat{j}+z\hat{k}=(-2λ+1)\hat{i}+(14λ+2)\hat{j}+(3λ+3)\hat{k}\\ \vec{r}=(\hat{i}+2\hat{j}+3\hat{k})+λ(-2\hat{i}+14\hat{j}+3\hat{k})$

Pregunta 17. Las ecuaciones cartesianas de una recta son 3x + 1 = 6y – 2 = 1 – z. Encuentre el punto fijo por el que pasa, sus razones de dirección y también su ecuación vectorial.

Solución:

Dada la ecuación de la línea es,

3x + 1 = 6y -2 = 1 – z

Dividiendo todo por 6

$=\frac{3x+1}{6}=\frac{6y-2}{6}=\frac{1-z}{6}\\ =\frac{3x}{6}+\frac{1}{6}=\frac{6y}{6}-\frac{2}{6}=\frac{1}{6}-\frac{z}{6}\\ =\frac{1}{2}x+\frac{1}{6}=y-\frac{1}{3}=-\frac{z}{6}+\frac{1}{6}\\ =\frac{1}{2}\left(x+\frac{1}{3}\right)=1\left(y-\frac{1}{3}\right)=\frac{1}{6}(z-1)\\ =\frac{x+\frac{1}{3}}{2}=\frac{y-\frac{1}{3}}{1}=\frac{z-1}{-6}=λ$

Comparándola con la ecuación de la recta ecuación de la recta que pasa por (x, ₁ y ₁ , z ₁ ) y las relaciones de dirección a, b, c,

$\frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{c}\\ (x_1,\ y_1,\ z_1)=\left(-\frac{1}{3},\ \frac{1}{3},\ 1\right)$

a = 2, b = 1, -6

Entonces, las relaciones de dirección de la línea son -2, 1, -6

De la ecuación (i)

$x = \left(2λ-\frac{1}{3}\right),\ y=\left(λ+\frac{1}{3}\right),\ z=(-6λ+1)$

Entonces, la ecuación vectorial de la recta dada es,

$x\hat{i}+y\hat{j}+z\hat{k}=\left(2λ-\frac{1}{3}\right)\hat{i}+\left(λ+\frac{1}{3}\right)\hat{j}+(-6λ+1)\hat{k}\\ \vec{r}=\left(-\frac{1}{3}\hat{i}+\frac{1}{3}\hat{j}+\hat{k}\right)+λ(2\hat{i}+\hat{j}-6\hat{k})$

Publicación traducida automáticamente

Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 12 Soluciones RD Sharma – Capítulo 28 La línea recta en el espacio – Ejercicio 28.1 | conjunto 2

Pregunta 11. Encuentra los cosenos directores de la recta $\frac{4-x}{2}=\frac{y}{6}=\frac{1-z}{3}$ . Además, redúcelo a forma vectorial.

Pregunta 12. Las ecuaciones cartesianas de una recta son x = ay + b, z = cy + d. Encuentre sus razones de dirección y redúzcalo a forma vectorial.

Pregunta 14. Encuentra los puntos en la recta $\frac{x+2}{3}=\frac{y+1}{2}=\frac{z-3}{2}$ a una distancia de 5 unidades de los puntos P(1, 3, 3).

Pregunta 15. Demostrar que los puntos cuyos vectores de posición son $-2\hat{i}+3\hat{j},\ \hat{i} + 2\hat{j}+3\hat{k}$ y $7\hat{i}-\hat{k}$ son colineales.

Pregunta 16. Encuentra las ecuaciones cartesianas y vectoriales de una recta que pasa por los puntos (1, 2, 3) y es paralela a la recta $\frac{-x-2}{1}=\frac{y+3}{7}=\frac{2z-6}{3}$

Pregunta 17. Las ecuaciones cartesianas de una recta son 3x + 1 = 6y – 2 = 1 – z. Encuentre el punto fijo por el que pasa, sus razones de dirección y también su ecuación vectorial.

Deja una respuesta Cancelar la respuesta

Pregunta 11. Encuentra los cosenos directores de la recta . Además, redúcelo a forma vectorial.

Pregunta 12. Las ecuaciones cartesianas de una recta son x = ay + b, z = cy + d. Encuentre sus razones de dirección y redúzcalo a forma vectorial.

Pregunta 13. Hallar la ecuación vectorial de una recta que pasa por el punto con vector de posición y paralela a la recta que une los puntos con vector de posición y . Además, encuentre el equivalente cartesiano de esta ecuación.

Pregunta 14. Encuentra los puntos en la recta a una distancia de 5 unidades de los puntos P(1, 3, 3).

Pregunta 15. Demostrar que los puntos cuyos vectores de posición son y son colineales.

Pregunta 16. Encuentra las ecuaciones cartesianas y vectoriales de una recta que pasa por los puntos (1, 2, 3) y es paralela a la recta

Pregunta 17. Las ecuaciones cartesianas de una recta son 3x + 1 = 6y – 2 = 1 – z. Encuentre el punto fijo por el que pasa, sus razones de dirección y también su ecuación vectorial.

Deja una respuesta Cancelar la respuesta

Pregunta 11. Encuentra los cosenos directores de la recta $\frac{4-x}{2}=\frac{y}{6}=\frac{1-z}{3}$ . Además, redúcelo a forma vectorial.

Pregunta 14. Encuentra los puntos en la recta $\frac{x+2}{3}=\frac{y+1}{2}=\frac{z-3}{2}$ a una distancia de 5 unidades de los puntos P(1, 3, 3).

Pregunta 15. Demostrar que los puntos cuyos vectores de posición son $-2\hat{i}+3\hat{j},\ \hat{i} + 2\hat{j}+3\hat{k}$ y $7\hat{i}-\hat{k}$ son colineales.

Pregunta 16. Encuentra las ecuaciones cartesianas y vectoriales de una recta que pasa por los puntos (1, 2, 3) y es paralela a la recta $\frac{-x-2}{1}=\frac{y+3}{7}=\frac{2z-6}{3}$