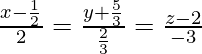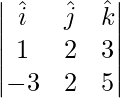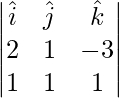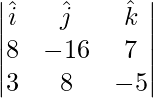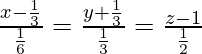Clase 12 RD Sharma Solutions – Capítulo 28 La línea recta en el espacio – Ejercicio 28.2 | conjunto 2

Posted on by Rudeus Greyrat

Pregunta 13. Encuentra las ecuaciones de la recta que pasa por el punto (−1, 2, 1) y paralela a la recta 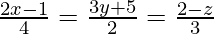 \frac{2x - 1}{4} = \frac{3y + 5}{2} = \frac{2 - z}{3} .

Solución:

La ecuación de la línea  \frac{2x - 1}{4} = \frac{3y + 5}{2} = \frac{2 - z}{3}  se puede reescribir como,

\frac{x - \frac{1}{2}}{2} = \frac{y + \frac{5}{3}}{\frac{2}{3}} = \frac{z - 2}{- 3}

Las relaciones de dirección de la línea paralela a la línea  \frac{2x - 1}{4} = \frac{3y + 5}{2} = \frac{2 - z}{3}  son proporcionales a 2, 2/3, -3.

La ecuación de la línea requerida que pasa por el punto (-1, 2, 1) que tiene relaciones de dirección proporcionales a (2, 2/3, -3) es,

\frac{x - \left( - 1 \right)}{2} = \frac{y - 2}{\frac{2}{3}} = \frac{z - 1}{- 3}

=> \frac{x + 1}{2} = \frac{y - 2}{\frac{2}{3}} = \frac{z - 1}{- 3}

Pregunta 14. Encuentra la ecuación de la recta que pasa por el punto (2, −1, 3) y es paralela a la recta 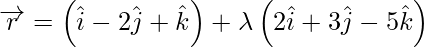 \overrightarrow{r} = \left( \hat{i} - 2 \hat{j} + \hat{k} \right) + \lambda\left( 2 \hat{i} + 3 \hat{j} - 5 \hat{k} \right) .

Solución:

La recta dada  \overrightarrow{r} = \left( \hat{i} - 2 \hat{j} + \hat{k} \right) + \lambda\left( 2 \hat{i} + 3 \hat{j} - 5 \hat{k} \right)  es paralela al vector 2 \hat{i} + 3 \hat{j} - 5 \hat{k}

Y la línea requerida también es paralela a la línea dada. 

Entonces, la línea requerida es paralela al vector 2 \hat{i} + 3 \hat{j} - 5 \hat{k}

Por tanto, la ecuación de la recta requerida que pasa por el punto (2,-1, 3) y es paralela al vector   2 \hat{i} + 3 \hat{j} - 5 \hat{k}  es, 

=> \overrightarrow{r} = \left( 2 \hat{i} - \hat{j} + 3 \hat{k} \right) + \lambda\left( 2 \hat{i} + 3 \hat{j} - 5 \hat{k} \right)

Pregunta 15. Encuentra las ecuaciones de la recta que pasa por el punto (2, 1, 3) y es perpendicular a las rectas 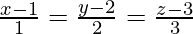 \frac{x - 1}{1} = \frac{y - 2}{2} = \frac{z - 3}{3}  y  \frac{x}{- 3} = \frac{y}{2} = \frac{z}{5} .

Solución:

Dejar,

\overrightarrow{b_1} = \hat{i} + 2 \hat{j} + 3 \hat{k}

\overrightarrow{b_2} = - 3 \hat{i} + 2 \hat{j} + 5 \hat{k}

Dado que la línea requerida es perpendicular a las líneas paralelas a los vectores   \overrightarrow{b_1}  y  \overrightarrow{b_2} , también es paralela al vector \overrightarrow{b} = \overrightarrow{b_1} \times \overrightarrow{b_2}   

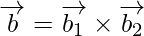
Ahora,  

\overrightarrow{b} = \overrightarrow{b_1} \times \overrightarrow{b_2}

= \begin{vmatrix}\hat{i} & \hat{j} & \hat{k} \\ 1 & 2 & 3 \\ - 3 & 2 & 5\end{vmatrix}

= 4 \hat{i} - 14 \hat{j} + 8 \hat{k}

= 2\left( 2 \hat{i} - 7 \hat{j} + 4 \hat{k} \right)

Por lo tanto, las relaciones de dirección de la línea requerida son proporcionales a 2, -7, 4. 

La ecuación de la línea requerida que pasa por el punto (2, 1, 3) y tiene relaciones de dirección proporcionales a 2, -7, 4 es 

=> \frac{x - 2}{2} = \frac{y - 1}{- 7} = \frac{z - 3}{4}

Pregunta 16. Halla la ecuación de la recta que pasa por el punto 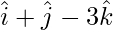 \hat{i} + \hat{j} - 3 \hat{k}  y es perpendicular a las rectas  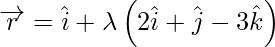\overrightarrow{r} = \hat{i} + \lambda\left( 2 \hat{i} + \hat{j} - 3 \hat{k} \right)  y  \overrightarrow{r} = \left( 2 \hat{i} + \hat{j} - \hat{ k} \right) + \mu\left( \hat{i} + \hat{j} + \hat{k} \right) .

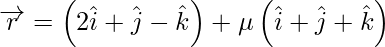Solución:

La línea requerida es perpendicular a las líneas paralelas a los vectores  \overrightarrow{b_1} = 2 \hat{i} + \hat{j} - 3 \hat{k}  y  \overrightarrow{b_2} = \hat{ i} + \hat{j}+ \hat{k} .

Entonces, la línea requerida es paralela al vector,

\overrightarrow{b} = \overrightarrow{b_1} \times \overrightarrow{b_2}

= \begin{vmatrix}\hat{i} & \hat{j} & \hat{k} \\ 2 & 1 & - 3 \\ 1 & 1 & 1\end{vmatrix}

= 4 \hat{i} - 5 \hat{j} + \hat{k}

Ecuación de la línea requerida que pasa por el punto  \left( \hat{i} + \hat{j} - 3 \hat{k} \right)  y es paralela a  \left( 4 \hat{i} - 5 \hat{j} + \hat{k} \right)  es,

=> \overrightarrow{r} = \left( \hat{i} + \hat{j} - 3 \hat{k} \right) + \lambda\left( 4 \hat{i} - 5 \hat{j} + \hat{k} \right)

Pregunta 17. Halla la ecuación de la recta que pasa por el punto (1, −1, 1) y es perpendicular a las rectas que unen los puntos (4, 3, 2), (1, −1, 0) y (1, 2, −1), (2, 1, 1).

Solución:

Las relaciones de dirección de la línea que une los puntos (4, 3, 2), (1, -1, 0) y (1, 2, -1), (2, 1, 1) son -3, -4, – 2 y 1, -1, 2 respectivamente.  

Dejar, 

\overrightarrow{b_1} = - 3 \hat{i} - 4 \hat{j} - 2 \hat{k}

\overrightarrow{b_2} = \hat{i} - \hat{j} + 2 \hat{k}

Como la línea requerida es perpendicular a las líneas paralelas a los vectores  \overrightarrow{b_1} = - 3 \hat{i} - 4 \hat{j} - 2 \hat{k}  y  \overrightarrow{b_2} = \hat{i} - \hat{j} + 2 \hat{k} , es paralela al vector \overrightarrow{b} = \overrightarrow{b_1} \times \overrightarrow{b_2}

Ahora,

\overrightarrow{b} = \overrightarrow{b_1} \times \overrightarrow{b_2}

= \begin{vmatrix}\hat{i} & \hat{j} & \hat{k} \\ - 3 & - 4 & - 2 \\ 1 & - 1 & 2\end{vmatrix}

= -10 \hat{i} + 4 \hat{j} + 7 \hat{k}

Entonces, las relaciones de dirección de la línea requerida son proporcionales a -10, 4, 7.

La ecuación de la línea requerida que pasa por el punto (1,-1, 1) y tiene relaciones de dirección proporcionales a -10, 4, 7 es  

=> \frac{x - 1}{- 10} = \frac{y + 1}{4} = \frac{z - 1}{7}

Pregunta 18. Determina las ecuaciones de la recta que pasa por el punto (1, 2, −4) y es perpendicular a las dos rectas 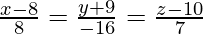 \frac{x - 8}{8} = \frac{y + 9}{- 16} = \frac{z - 10}{7}  y  \frac{x - 15}{3} = \frac{y - 29}{8} = \frac{z - 5}{- 5} .

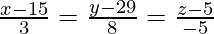Solución:

Tenemos,

\frac{x - 8}{8} = \frac{y + 9}{- 16} = \frac{z - 10}{7}

\frac{x - 15}{3} = \frac{y - 29}{8} = \frac{z - 5}{- 5}

Dejar,

\overrightarrow{b_1} = 8 \hat{i} - 16 \hat{j} + 7 \hat{k}

\overrightarrow{b_2} = 3 \hat{i} + 8 \hat{j} - 5 \hat{k}

Como la línea requerida es perpendicular a las líneas paralelas a los vectores  \overrightarrow{b_1}  y  \overrightarrow{b_2} , es paralela al vector \overrightarrow{b} = \overrightarrow{b_1} \times \overrightarrow{b_2}

Ahora,  

\overrightarrow{b} = \overrightarrow{b_1} \times \overrightarrow{b_2}

= \begin{vmatrix}\hat{i} & \hat{j} & \hat{k} \\ 8 & - 16 & 7 \\ 3 & 8 & - 5\end{vmatrix}

= 24 \hat{i} + 61 \hat{j} + 112 \hat{k}

Las relaciones de dirección de la línea requerida son proporcionales a 24, 61, 112. 

La ecuación de la línea requerida que pasa por el punto (1, 2, -4) y tiene relaciones de dirección proporcionales a 24, 61, 112 es,

=> \frac{x - 1}{24} = \frac{y - 2}{61} = \frac{z + 4}{112}

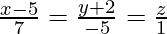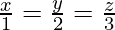Pregunta 19. Demuestra que las rectas  \frac{x - 5}{7} = \frac{y + 2}{- 5} = \frac{z}{1}  y  \frac{x}{1} = \frac{y}{2} = \frac{z}{3}  son perpendiculares entre sí.

Solución:

Las relaciones de dirección de la línea  \frac{x - 5}{7} = \frac{y + 2}{- 5} = \frac{z}{1}  son proporcionales a 7, -5, 1 respectivamente.  

Y las relaciones de dirección de la línea  \frac{x}{1} = \frac{y}{2} = \frac{z}{3}  son proporcionales a 1, 2, 3 respectivamente.  

Dejar,

\overrightarrow{b_1} = 7 \hat{i} - 5 \hat{j} + \hat{k}

\overrightarrow{b_2} = \hat{i} + 2 \hat{j} + 3 \hat{k}

Ahora, 

\overrightarrow{b_1} . \overrightarrow{b_2} = \left( 7 \hat{i} - 5 \hat{j} + \hat{k} \right) . \left( \hat{i} + 2 \hat{j} + 3 \hat{k} \right)

= 7 – 10 + 3

= 0

Asi que, \overrightarrow{b_1} \perp \overrightarrow{b_2}

Por lo tanto, las rectas dadas son perpendiculares entre sí.

Por lo tanto probado.

Pregunta 20. Encuentra la ecuación vectorial de la recta que pasa por el punto (2, −1, −1) que es paralela a la recta 6x − 2 = 3y + 1 = 2z − 2. 

Solución:

La ecuación de la línea 6x − 2 = 3y + 1 = 2z − 2 se puede reescribir como

\frac{x - \frac{1}{3}}{\frac{1}{6}} = \frac{y + \frac{1}{3}}{\frac{1}{3}} = \frac{z - 1}{\frac{1}{2}}

=> \frac{x - \frac{1}{3}}{1} = \frac{y + \frac{1}{3}}{2} = \frac{z - 1}{3}

Dado que la línea requerida es paralela a la línea dada, las relaciones de dirección de la línea requerida son proporcionales a 1,2,3.

La ecuación vectorial de la línea requerida que pasa por el punto (2,-1,-1) y tiene relaciones de dirección proporcionales a 1,2,3 es,

=> \overrightarrow{r} = \left( 2 \hat{i} - \hat{j} - \hat{k} \right) + \lambda\left( \hat{i} + 2 \hat{j} + 3 \hat{k} \right)

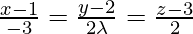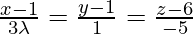Pregunta 21. Si las rectas  \frac{x - 1}{- 3} = \frac{y - 2}{2 \lambda} = \frac{z - 3}{2}  y  \frac{x - 1}{3\lambda} = \frac{y - 1}{1} = \frac{z - 6}{- 5}  son perpendiculares, encuentra el valor de λ.

Solución:

Las ecuaciones de las rectas dadas son,

\frac{x - 1}{- 3} = \frac{y - 2}{2 \lambda} = \frac{z - 3}{2}

\frac{x - 1}{3\lambda} = \frac{y - 1}{1} = \frac{z - 6}{- 5}

Como las rectas dadas son perpendiculares entre sí, tenemos  

=> -3 (3λ) + 2λ (1) + 2 (-5) = 0

=> -9λ + 2λ – 10 = 0

=> -7λ = 10

=> λ = -10/7

Por tanto, el valor de λ es -10/7.

Pregunta 22. Si las coordenadas de los puntos A, B, C, D son (1, 2, 3), (4, 5, 7), (−4, 3, −6) y (2, 9, 2) respectivamente, luego encuentre el ángulo entre las líneas AB y CD. 

Solución:

Las relaciones de dirección de AB y CD son proporcionales a 3, 3, 4 y 6, 6, 8, respectivamente.

Sea θ el ángulo entre AB y CD. Después,

\cos \theta = \frac{3 \times 6 + 3 \times 6 + 4 \times 8}{\sqrt{3^2 + 3^2 + 4^2} \sqrt{6^2 + 6^2 + 8^2}}

= \frac{68}{\sqrt{34} \sqrt{136}}

= 1

Ahora cos θ = 1

=> θ = 0°

Por lo tanto, el ángulo entre AB y CD es 0°.

Pregunta 23. Encuentra el valor de λ para que las siguientes líneas sean perpendiculares entre sí. 

\frac{x - 5}{5\lambda + 2} = \frac{2 - y}{5} = \frac{1 - z}{- 1}, \frac{x}{1} = \frac{2y + 1}{4\lambda} = \frac{1 - z}{- 3}

Solución:

La ecuación de la línea dada  \frac{x - 5}{5\lambda + 2} = \frac{2 - y}{5} = \frac{1 - z}{- 1}  se puede reescribir como,

\frac{x - 5}{5\lambda + 2} = \frac{y - 2}{- 5} = \frac{z - 1}{1}

La ecuación de la línea dada  \frac{x}{1} = \frac{2y + 1}{4\lambda} = \frac{1 - z}{- 3}  se puede reescribir como, 

\frac{x}{1} = \frac{y + \frac{1}{2}}{2\lambda} = \frac{z - 1}{3}

Como las rectas dadas son perpendiculares entre sí, tenemos  

=> (5λ + 2) (1) – 5 (2λ) + 1 (3) = 0

=> 5λ + 2 – 10λ + 3 = 0

=> -5λ = -5

=> λ = 1

Por lo tanto, el valor de λ es 1.

Pregunta 24. Halla los cosenos directores de la recta 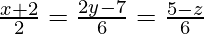 \frac{x + 2}{2} = \frac{2y - 7}{6} = \frac{5 - z}{6} . Además, encuentra la ecuación vectorial de la línea que pasa por el punto A(−1, 2, 3) y es paralela a la línea dada.  

Solución:

La ecuación de la recta dada es,

\frac{x + 2}{2} = \frac{2y - 7}{6} = \frac{5 - z}{6}

La ecuación dada se puede reescribir como

\frac{x + 2}{2} = \frac{y - \frac{7}{2}}{3} = \frac{z - 5}{- 6}

Esta línea pasa por el punto (-2, 7/2, 5) y tiene relaciones de dirección proporcionales a 2, 3, −6. 

Entonces, sus cosenos directores son \left(\frac{2}{\sqrt{2^2 + 3^2 + \left( - 6 \right)^2}}, \frac{3}{\sqrt{2^2 + 3^2 + \left( - 6 \right)^2}}, \frac{- 6}{\sqrt{2^2 + 3^2 + \left( - 6 \right)^2}}\right)  

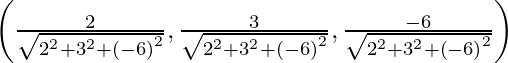
O, \left(\frac{2}{7}, \frac{3}{7}, \frac{- 6}{7}\right)

La línea requerida pasa por el punto que tiene el vector de posición  \overrightarrow{a} = - \hat{i} + 2 \hat{j} + 3 \hat{k} .

Y también es paralelo al vector  \overrightarrow{b} = 2 \hat{i} + 3 \hat{j} - 6 \hat{k} .

Entonces, su ecuación vectorial es,

=> \overrightarrow{r} = \left( - \hat{i} + 2 \hat{j} + 3 \hat{k} \right) + \lambda\left( 2 \hat{i} + 3 \hat{j} - 6 \hat{k} \right)

Publicación traducida automáticamente

Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *