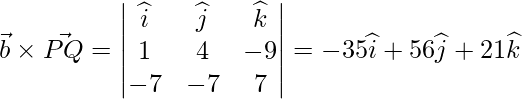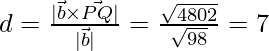Clase 12 RD Sharma Solutions – Capítulo 28 La línea recta en el espacio – Ejercicio 28.4

Posted on by Rudeus Greyrat

Pregunta 1. Encuentra la distancia perpendicular del punto (3, -1, 11) desde la línea 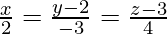\frac{x}{2}=\frac{y-2}{-3}=\frac{z-3}{4}

Solución:

Sea Q el pie de la perpendicular trazada desde P (3, -1, 11) a la línea   \frac{x}{2}=\frac{y-2}{-3}=\frac{z-3}{4} , entonces tenemos que encontrar la longitud de PQ es el punto general en la línea \frac{x}{2}=\frac{y-2}{-3}=\frac{z-3}{4}=\lambda (say)

Coordenada de Q =  (2\lambda,-3\lambda+2,4\lambda+3) , relaciones de dirección de la línea dada = 2,-3,4. Dado que PQ es la interfaz perpendicular a la línea dada. 

a_1a_2+b_1b_2+c_1c_2=0

\Rightarrow 2(2\lambda-3)+(-3 )(-3\lambda+3)4(4\lambda-8)=0

\Rightarrow 4\lambda-6+9\lambda-9+16\lambda-32=0

29\lambda-47=0; \lambda = \frac{47}{29}

Entonces, las coordenadas de Q son:

\Rightarrow 2(\frac{47}{29}),-3(\frac{47}{29})+2,4(\frac{47}{29})+3 = \frac{94}{29},\frac{-83}{29},\frac{275}{29}

La distancia entre P y Q se da como:

= \sqrt{(\frac{94}{29}-3)^2+(\frac{-83}{29}+1)^2+(\frac{275}{29}-11)^2}

= \sqrt{(\frac{7}{29})^2+(\frac{-54}{29})^2+(\frac{-44}{29})^2}

=\sqrt{\frac{49}{841}+\frac{2916}{841}+\frac{1936}{841}}

=\sqrt{\frac{4901}{841}}

Entonces, la distancia requerida es  \sqrt{\frac{4901}{841}} unidades

Pregunta 2. Encuentra la distancia perpendicular del punto (1,0,0) desde la línea 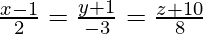 \frac{x-1}{2}=\frac{y+1}{-3}=\frac{z+10}{8} . Además, encuentre las coordenadas del pie de la perpendicular y la ecuación de la perpendicular.

Solución:

Consideremos el pie de la perpendicular trazada desde P (1,0,0) hasta la línea  \frac{x-1}{2}=\frac{y+1}{-3}=\frac{z+10}{8} Q. Así que encontremos la longitud de PQ, es decir \frac{x-1}{2}=\frac{y+1}{-3}=\frac{z+10}{8}=\lambda

Coordenada de Q = (2\lambda+1, -3\lambda-1, 8\lambda-10)

Las relaciones de dirección de la línea dada:  a_1a_2+b_1b_2+c_1c_2=0

\Rightarrow 2(2\lambda)+(-3)(-3\lambda-1)+8(8\lambda-10)=0

4\lambda+9\lambda+3+64\lambda-80=0

\Rightarrow 77\lambda-77=0; \lambda = 1

Entonces las coordenadas de Q son las siguientes:

(2\lambda+1, -3\lambda-1, 8\lambda-10)= [2(1)+1,-3(1)-1,8(1)-10]= [3,4,-2]

La distancia entre P y Q viene dada por:

PQ = \sqrt{(x1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}

PQ = \sqrt{(1-3)^2+(0+4)^2+(0+2)^2}=\sqrt{4+16+4}

PQ = \sqrt{24} = 2\sqrt{6}

Por tanto, el pie de la perpendicular = (3,-4,-2);

Longitud de la perpendicular =  2\sqrt{6} unidades.

Pregunta 3. Encuentra el pie de la perpendicular trazada desde el punto A(1,0,3) hasta la unión de los puntos B(4,7,1) y C(3,5,3).

Solución:

Consideremos, el pie de la perpendicular trazada desde A(1,0,3) hasta la línea que une

Los puntos B(4,7,1) y C(3,5,3) sean D. La ecuación de la recta que pasa por 

los puntos B(4,7,1) y C(3,5,3) es 

\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}

\Rightarrow \frac{x-4}{3-4}=\frac{y-7}{5-7}=\frac{z-1}{3-1}

\Rightarrow \frac{x-4}{-1}=\frac{y-7}{-2}=\frac{z-1}{2}

Dejar \frac{x-4}{-1}=\frac{y-7}{-2}=\frac{z-1}{2}=\lambda

Entonces, la relación de dirección de AD es (-\lambda+4-1),(-2\lambda+7-0),(2\lambda+1-3) = (-\lambda+3),(-2\lambda+7),(2\lambda-2)

La recta AD es la perpendicular a BC por lo que, a_1a_2+b_1b_2+c_1c_2=0

\Rightarrow -1(-\lambda+3)+(2)(-2\lambda+7)+2(2\lambda-2)=0

\Rightarrow 9\lambda -21 = 0; \lambda = \frac{21}{9}

Por lo tanto, las coordenadas de D son: \left(\frac{-21}{9}+4,(-2)(\frac{21}{9}+7),2(\frac{21}{9}+1)\right)

= \left(\frac{15}{9},\frac{21}{9},\frac{51}{9}\right) = \left(\frac{5}{3},\frac{7}{3},\frac{17}{3}\right)

Pregunta 4. A (1,0,4), B (0,-11,3), C (2,-3,1) son tres puntos y D es el pie de la perpendicular de A sobre BC. Encuentre las coordenadas de D.

Solución:

Dado: D es la perpendicular desde A(1,0,4) sobre BC. Asi que,

La ecuación de la recta que pasa por BC es:

\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}

\frac{x-0}{2-0}=\frac{y+11}{-3+11}=\frac{z-3}{1-3}

\frac{x}{2}=\frac{y+11}{8}=\frac{z-3}{-2}

\frac{x}{2}=\frac{y+11}{8}=\frac{z-3}{-2}=\lambda

Coordenadas de D = (  2\lambda, 8\lambda-11,-2\lambda+3 )

Las relaciones de dirección de AD son (2\lambda-1),(8\lambda-11-0),(-2\lambda+3-4)= (2\lambda-1),(8\lambda-11),(-2\lambda-1)

La recta AD es perpendicular a BS entonces, 

a_1a_2+b_1b_2+c_1c_2=0

2(2\lambda-1)+8(8\lambda-11)+(-2)(-2\lambda-1)=0

72\lambda-88 = 0; \lambda = \frac{88}{72} or \frac{11}{9}

Entonces, las coordenadas de D son = (2\lambda,8\lambda-11,-2\lambda+3)

\left(2(\frac{11}{9}),8(\frac{11}{9})-11,-2(\frac{11}{9})+3\right) =

\left(\frac{22}{9},\frac{-11}{9},\frac{5}{9}\right)

Pregunta 5. Halla el pie de la perpendicular desde el punto (2,3,4) hasta la recta 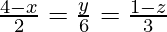 \frac{4-x}{2}=\frac{y}{6}=\frac{1-z}{3} . Además, encuentre la distancia perpendicular desde el punto dado a la línea.

Solución:

Consideremos que El pie de la perpendicular trazada desde P(2,3,4) hasta la recta

\frac{4-x}{2}=\frac{y}{6}=\frac{1-z}{3} es  \theta _

La ecuación de la recta es  \frac{4-x}{2}=\frac{y}{6}=\frac{1-z}{3}

Dejar \frac{x-4}{-2}=\frac{y}{6}=\frac{z-1}{-3} = \lambda

Coordenadas de Q = (-2\lambda+4-2),(6\lambda-3),(-3\lambda+1-4) = (-2\lambda+2),(6\lambda-3),(-3\lambda-3)

Entonces, PQ es perpendicular a la recta dada,  a_1a_2+b_1b_2+c_1c_2=0

(-2)(-2\lambda+2)+6(6\lambda-3)+(-3)(-3\lambda-3)=0

49\lambda-13=0; \lambda=\frac{13}{49}

Coordenadas de Q = (-2\lambda+4, 6\lambda. -3\lambda+1)

= \left(-2(\frac{13}{49})+4,6(\frac{13}{49}),-3(\frac{13}{49})+1\right)

= \left(\frac{-26+196}{49},\frac{78}{49},\frac{-39+49}{49}\right)= \left(\frac{170}{49}, \frac{78}{49},\frac{10}{49}\right)

La distancia entre P y Q viene dada por y: PQ = \sqrt{(x1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}

= \sqrt{(\frac{170}{49}-2)^2+(\frac{78}{49}-3)^2+(\frac{10}{49}-4)^2}

= \sqrt{\frac{44541}{2401}} = \sqrt{\frac{909}{49}} = \frac{3\sqrt{101}}{49}

Por lo tanto, la distancia perpendicular de (2,3,4) a la línea dada es  \frac{3\sqrt{101}}{49} unidades.

Pregunta 6. Halla la ecuación de la perpendicular trazada desde el punto P (2,4,-1) hasta la recta 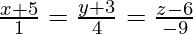 \frac{x+5}{1}=\frac{y+3}{4}=\frac{z-6}{-9} . Además, anota las coordenadas del pie de la perpendicular desde P.

Solución:

Sea  \theta  el pie de la perpendicular trazada desde P(2,4,-1) a la recta

\frac{x+5}{1}=\frac{y+3}{4}=\frac{z-6}{-9}

la línea dada es \frac{x+5}{1}=\frac{y+3}{4}=\frac{z-6}{-9} = \lambda (say)

Coordenada de Q (Punto general sobre la recta) = (\lambda-5, 4\lambda-3, -9\lambda+6)

Las relaciones de dirección de PQ son: (\lambda-5-2),(4\lambda-3-4),(-9\lambda+6+1) = \lambda-7, 4\lambda-7, -9\lambda+7

Como la recta PQ es perpendicular a la recta dada, entonces: a_1a_2+b_1b_2+c_1c_2=0

1(\lambda-7)+4(4\lambda-7)+(-9)(-9\lambda+7)=0

98\lambda-98=0; \lambda=1

Por lo tanto, coordenadas de pie de perpendicular = {-4, 1, -3}

Entonces la ecuación de la perpendicular PQ es: \frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}

\Rightarrow \frac{x-2}{-4-2}=\frac{y-4}{1-4}=\frac{z+1}{-3+1}

\Rightarrow \frac{x-2}{-6}=\frac{y-4}{-3}=\frac{z+1}{-2}

Pregunta 7. Halla la longitud de la perpendicular trazada desde el punto (5,4,-1) hasta la recta 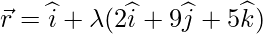\vec{r}=\widehat{i} + \lambda(2\widehat{i} + 9\widehat{j}+5\widehat{k})

Solución:

Sea Q el pie de la perpendicular trazada desde P(5,4,-1) hasta la línea dada, por lo que la ecuación de la línea dada es:

\vec{r}=\widehat{i} + \lambda(2\widehat{i} + 9\widehat{j}+5\widehat{k})

(x\widehat{i}+y\widehat{j}+z\widehat{k}) = (1+2\lambda)\widehat{i}+(9\lambda)\widehat{j}+(5\lambda)\widehat{k}

Igualando los coeficientes de \widehat{i}, \widehat{j}, \widehat{k}

\Rightarrow x = 1+2\lambda, y = 9\lambda, z = 5\lambda

\Rightarrow \frac{x-1}{2} = \lambda, \frac{y}{9} = \lambda, \frac{z}{5}=\lambda

\Rightarrow \frac{x-1}{2} = \frac{y}{9} =\frac{z}{5}=\lambda (say)

Coordenada de Q = (2\lambda+1,9\lambda,5\lambda)

Las relaciones de dirección de la línea PQ son: (2\lambda+1-5),9\lambda-4,5\lambda+1

\Rightarrow 2\lambda-4, 9\lambda-4, 5\lambda+1

Como la recta PQ es perpendicular a la recta dada, entonces: a_1a_2+b_1b_2+c_1c_2=0

2(2\lambda-4)+9(9\lambda-4)+5(5\lambda+1)=0

\Rightarrow 4\lambda - 8 +81\lambda - 36 +25\lambda + 5 = 0

\Rightarrow 110\lambda - 39 = 0; \lambda = \frac{39}{110}

Coordenada de Q = {  2\lambda+1, 9\lambda, 5\lambda  }

= \left(2(\frac{39}{110})+1,9(\frac{39}{110}),5(\frac{39}{110})\right)

= \left(\frac{188}{110},\frac{351}{110},\frac{195}{110}\right)

Longitud de la perpendicular = PQ = \sqrt{(x1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}

= \sqrt{(5-\frac{188}{110})^2+ (4-\frac{351}{110})^2+(-1-\frac{195}{110})^2}

  PQ = \sqrt{\frac{231990}{12100}} or \sqrt{\frac{2109}{110}}  

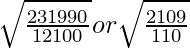
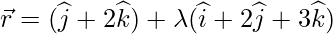Pregunta 8. Halla el pie de la perpendicular trazada desde el punto  \widehat{i}+6\widehat{j}+3\widehat{k}  hasta la recta  \vec{r} = (\widehat{j}+2\widehat{k}) + \lambda(\widehat{i}+2\widehat{j}+3\widehat{k}) . Además, encuentre la longitud de la perpendicular.   

Solución:

 Sea Q  el vector de posición del pie de la perpendicular trazada desde p  (\widehat{i}+6\widehat{j}+3\widehat{k}) sobre  . Entonces, Q está en la línea \vec{r} = (\widehat{j}+2\widehat{k}) + \lambda(\widehat{i}+2\widehat{j}+3\widehat{k}) (\vec{q}) \vec{r} = (\widehat{j}+2\widehat{k}) + \lambda(\widehat{i}+2\widehat{j}+3\widehat{k})

Entonces, el vector de posición de Q = \lambda(\widehat{i})+(1+2\lambda)\widehat{j}+(2+3\lambda)\widehat{k}

\vec{PQ} es el vector de posición de Q – vector de posición de p = (\lambda\widehat{i}+(1+2\lambda)\widehat{j}-(\widehat{i}+6\widehat{j}+3\widehat{k})

\vec{PQ} = (\lambda-1)\widehat{i}+(2\lambda-5)\widehat{j}+(3\lambda-1)\widehat{k}

Aquí, el vector PQ es perpendicular a la línea dada . Asi que,

(\lambda-1)\widehat{i}+(2\lambda-5)\widehat{j}+(3\lambda-1)\widehat{k} = 0  

\Rightarrow (\lambda-1)1+(2\lambda-5)2+(3\lambda-1)3 = 0

14\lambda -14 = 0; \lambda = 1

Vector de posición de Q = { (\widehat{j}+2\widehat{j})+\lambda(\widehat{i}+2\widehat{j}+3\widehat{k}) }

= (\widehat{j}+2\widehat{k})+1(\widehat{i}+2\widehat{j}+3\widehat{k})

Pie de la perpendicular = \widehat{i}+3\widehat{j}+5\widehat{k}

\vec{PQ} = Vector de posición de Q – Vector de posición de P

= (\widehat{i}+3\widehat{j}+5\widehat{k})-(\widehat{i}+6\widehat{j}+3\widehat{k})

= -3\widehat{i}+2\widehat{k}

|\vec{PQ}|  =  \sqrt{(-3)^2+(2)^2} = \sqrt{13}  unidades

Pregunta 9. Encuentra la ecuación del drwan peprendicular desde el punto P (-1,3,2) hasta la recta 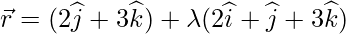 \vec{r} = (2\widehat{j}+3\widehat{k})+\lambda(2\widehat{i}+\widehat{j}+3\widehat{k})   . Además, encuentre las coordenadas del pie de la perpendicular desde P.

Solución:

Sea Q la perpendicular trazada desde P { -\widehat{i}+3\widehat{j}+2\widehat{k} } sobre la 

vector \vec{r} = (2\widehat{j}+3\widehat{k})+\lambda(2\widehat{i}+\widehat{j}+3\widehat{k})

Sea el vector de posición de Q : (2\widehat{i}+3\widehat{k})+ \lambda(2\widehat{i}+\widehat{j}+3\widehat{k})

                                                      :  (2\lambda)\widehat{i}+(2+\lambda)\widehat{j}+(3+3\lambda)\widehat{k}

\vec{PQ} = Vector de posición de Q – Vector de posición de P = (2\lambda)\widehat{i}+(2+\lambda)\widehat{j}+(3+3\lambda)\widehat{k} - (-\widehat{i}+3\widehat{j}+2\widehat{k})

\vec{PQ} = (2\lambda+1)\widehat{i} + (\lambda-1)\widehat{j}+(3\lambda+1)\widehat{k}

Como el vector PQ es perpendicular a la recta dada, 

(2\lambda+1)\widehat{i} + (\lambda-1)\widehat{j}+(3\lambda+1)\widehat{k} = 0

4\lambda+2+\lambda-1+9\lambda+3 = 0; \lambda= \frac{-4}{14} or \frac{-2}{7}

Vector de posición de Q =  (2\lambda)\widehat{i}+(2+\lambda)\widehat{j}+(3+3\lambda)\widehat{k}  es

2(\frac{-2}{7})\widehat{i}+(2-\frac{2}{7})\widehat{j}+(3+3(\frac{-2}{7})\widehat{k})

\frac{-4}{7}\widehat{i}+\frac{12}{7}\widehat{j}+\frac{15}{7}\widehat{k}

Coordenadas de pie de la perpendicular: \left(\frac{-4}{7},\frac{12}{7},\frac{15}{7}\right)

La ecuación de PQ es: \vec{r} = \vec{a}+\lambda(\vec{b}-\vec{a})

\Rightarrow \vec{r} = (-\widehat{i}+3\widehat{j}+2\widehat{k})+\lambda((\frac{-4}{7}\widehat{i}+\frac{12}{7}\widehat{j}+\frac{15}{7}\widehat{k})-(-\widehat{i}+3\widehat{j}+2\widehat{k}))

\vec{r} = (-\widehat{i}+3\widehat{j}+2\widehat{k}) + \lambda(\frac{3}{7}\widehat{i}-\frac{9}{7}\widehat{j}+\frac{1}{7}\widehat{k})

\vec{r} = (-\widehat{i}+3\widehat{j}+2\widehat{k}) + \mu(3\widehat{i}-9\widehat{j}+\widehat{k})

Pregunta 10. Encuentra el pie de la perpendicular desde (0,2,7) en la línea 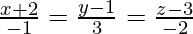\frac{x+2}{-1}=\frac{y-1}{3}=\frac{z-3}{-2}

Solución:

Sea Q el pie de la perpendicular trazada desde (0,2,7) hasta la recta   \frac{x+2}{-1}=\frac{y-1}{3}=\frac{z-3}{-2}  . 

Dada la ecuación de la recta es \frac{x+2}{-1}=\frac{y-1}{3}=\frac{z-3}{-2} = \lambda (say)

Coordenada de Q = { -\lambda-2, 3\lambda+1, -2\lambda+3 } 

Las relaciones de dirección de PQ son  (\lambda-2-0), (3\lambda+1-2), (-2\lambda+3-7) = (-\lambda-2),(3\lambda-1),(-2\lambda- 4)

Como PQ es perpendicular a la recta dada, entonces a_1a_2+b_1b_2+c_1c_2=0

-1(-\lambda-2)+3(3\lambda-1)+(-2)(-2\lambda-4)=0

\Rightarrow \lambda+2+9\lambda-3+4\lambda+8=0

\Rightarrow 14\lambda + 7 =0; \lambda = \frac{-1}{2}

Pie de la perpendicular = { \lambda-2, 3\lambda+1, -2\lambda+3 }\

= \left(-(\frac{-1}{2})-2, 3(\frac{-1}{2}),-2(\frac{-1}{2})+3\right)

\left(\frac{-3}{2}, \frac{-1}{2}, 4\right)

Pregunta 11. Encuentra el pie de la perpendicular desde (1,2,-3) a la recta 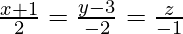\frac{x+1}{2}=\frac{y-3}{-2}=\frac{z}{-1}

Solución:

Sea Q el pie de la perpendicular desde P (1,2,-3) a la recta   \frac{x+1}{2}=\frac{y-3}{-2}=\frac{z}{-1}  .

Dada la ecuación de la línea es \frac{x+1}{2}=\frac{y-3}{-2}=\frac{z}{-1} =\lambda (say)

\Rightarrow x = 2\lambda-1, y=-2\lambda+3, z = -\lambda

Las coordenadas de Q son { 2\lambda-1, -2\lambda+3, -\lambda }

Las relaciones de dirección de PQ son:   (2\lambda-1-1), (-2\lambda+3-2), (-\lambda+3)  =

(2\lambda-2), (-2\lambda+1), (-\lambda+3)

Sea PQ la perpendicular a la línea dada, entonces a_1a_2+b_1b_2+c_1c_2=0

2(2\lambda-2)+(-2)(-2\lambda+1)+(-1)(-\lambda+3)=0

9\lambda-9 = 0; \lambda = 1

Coordenada de la perpendicular: (2\lambda-1, -2\lambda+3, -\lambda)

\Rightarrow (2(1)-1, -2(1)+3, -1) = (1,1,-1)

Pregunta 12. Encuentra la ecuación de la recta que pasa por los puntos A (0,6,-9) y B (-3, 6, 3). Si D es el pie de la perpendicular trazada desde un punto C (7,4,-1) sobre la línea AB, entonces encuentre las coordenadas del punto D y la ecuación de la línea CD.

Solución:

La ecuación de la recta AB es  \frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}

\Rightarrow \frac{x-0}{3-0}=\frac{y-6}{-6-6}=\frac{z+9}{3+9}

\Rightarrow \frac{x-0}{3-0}=\frac{y-6}{-6-6}=\frac{z+9}{3+9} = \lambda (say)

Coordenada del punto D = { -3\lambda, -12\lambda+6, 12\lambda-9 }

Relaciones de dirección de CD = (-3\lambda-7)+(-12)(-12\lambda+6-4)+12(12\lambda-9+1)

= (-3\lambda-7)+(-12)(-12\lambda+2)+12(12\lambda-8)

Como la línea CD es perpendicular a la línea AB, entonces  a_1a_2+b_1b_2+c_1c_2=0

-3(-3\lambda-7)+(-12)(-12\lambda+2)+12(12\lambda-8) =0

297\lambda-99=0; \lambda = \frac{1}{3}

Coordenada de D = { -3\lambda, -12\lambda+6, 12\lambda-9 }

= { -3(\frac{1}{3}), -12(\frac{1}{3})+6, 12(\frac{1}{3})-9 }

= (-1,2,-5)

La ecuación de CD es \frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}  

\Rightarrow \frac{x-7}{-1-7}=\frac{y-4}{2-4}=\frac{z+1}{-5+1}

\Rightarrow \frac{x-7}{-8}=\frac{y-4}{-2}=\frac{z+1}{-4}

\Rightarrow \frac{x-7}{4}=\frac{y-4}{1}=\frac{z+1}{2}

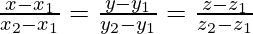
Pregunta 13. Encuentra la distancia del punto (2,4,-1) de la línea 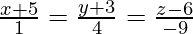\frac{x+5}{1}=\frac{y+3}{4}=\frac{z-6}{-9}

Solución:

Sea P = (2,4,-1)

Para encontrar la distancia necesitamos encontrar un punto Q en la línea. Vemos que la línea está pasando 

el punto Q(-5,-3,6). Entonces, tomemos este punto como el punto requerido. 

La recta también es paralela al vector. \vec{b} = \widehat{i} +4\widehat{j} -9\widehat{k}

Ahora,  \vec{PQ}  = (-5\widehat{i}-3\widehat{j}+6\widehat{k})-(2\widehat{i}+4\widehat{j}-\widehat{k})=-7\widehat{i}-7\widehat{j}+7\widehat{k}

\vec{b} \times \vec{PQ} = \begin{vmatrix} \widehat{i} & \widehat{j} & \widehat{k} \\ 1 & 4 & -9 \\ -7 & -7 & 7 \end{vmatrix}= -35\widehat{i}+56\widehat{j}+21\widehat{k}

|\vec{b} \times \vec{PQ}| = \sqrt{1225+3136+441} = \sqrt{4802}

\vec{b} = \sqrt{1+16+81} = \sqrt{98}

Por lo tanto, d= \frac{|\vec{b} \times \vec{PQ}|}{|\vec{b}|} = \frac{\sqrt{4802}}{\sqrt{98}}=7

Pregunta 14. Halla las coordenadas del pie de la perpendicular trazada desde el punto A (1,8,4) hasta la recta que une los puntos B (0,-1,3) y C (2,-3,-1).

Solución:

Sea L el pie de la perpendicular trazada desde A(1,8,4) sobre la recta que une los puntos B(0,-1,3) y C(2,-3,-1). 

La ecuación de la recta que pasa por los puntos B y C viene dada por 

\vec{r}=\vec{b}+\lambda(\vec{c}-\vec{b})

\vec{r} = (0+2\lambda)\widehat{i}+(-1-2\lambda)\widehat{j}+(3-4\lambda)\widehat{k}

Sea el vector de posición de L, 

\vec{r}=(2\lambda)\widehat{i}+(-1-2\lambda)\widehat{k}+(3-4\lambda)\widehat{k}......(Equation 1)

Entonces,  \vec{AL}  = Vector de posición de L – Vector de posición de A

\Rightarrow \vec{AL} = (2\lambda)\widehat{i}+(-1-2\lambda)\widehat{j}+(3-4\lambda)\widehat{k}-(1\widehat{i}+8\widehat{j}+4\widehat{k})

Como el vector AL es perpendicular a la recta dada

que es paralelo a \vec{b}=2\widehat{i}-2\widehat{j}-4\widehat{k}

Por lo tanto, \vec{AL}\cdot\vec{b}=0

\Rightarrow 2(-1+2\lambda)-2(-9-2\lambda)-4(-1-4\lambda)=0

24\lambda+20=0; \lambda=\frac{-5}{6}

Poniendo el valor de lambda en la Ecuación 1, obtenemos:

\vec{r} = \frac{-5}{3}\widehat{i}+\frac{2}{3}\widehat{j}+\frac{19}{3}\widehat{k}

Entonces, las coordenadas del pie de la perpendicular son

 \left(\frac{-5}{3}, \frac{2}{3}, \frac{19}{3}\right)

Publicación traducida automáticamente

Artículo escrito por versatile1990 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *